
Лазеры и волоконная оптика в биомедицинских исследованиях
.pdf92 |
Гл. 1. Основы лазерной биомедицины |
пузырчатости и дезинтеграцию мембраны. В идеальном случае терапевтическая доза лежит где-то между этими крайними случаями, где проницаемость клетки является обратимой и клетка восстанавливается к нормальному состоянию в течение секунд или минут после окончания операции. Однако в реальных условиях терапевтическая доза и избыточная доза немного перекрываются, поэтому выживаемость клеток обычно меньше 100 %.
Типичные лазерные источники для прицельной оптической инжекции или трансфекции включают 800-нанометровые фемтосекундные импульсные титан-сапфировые лазеры и лазерные источники непрерывного излучения на 405 и 488 нм. Наносекундные импульсные Nd:YAG-лазеры с длиной волны 1064 нм также используются для целевой трансфекции, хотя более часто они применяются при нецелевой оптической трансфекции. Основные параметры лазеров и экспериментальные данные для оптической инжекции и трансфекции биологических препаратов в клетки животных и человека представлены в табл. 1.10 [424].
Основные области применений лазеров в фотомедицине, а также инструменты и приборы, реализующие лазерные методы диагностики, терапии и хирургии, представлены в табл. 1.11. Области медицинских применений мощных волоконных лазеров, активированных Yb (0,97 мкм ), Nd (1,06 мкм), Er (1,56 мкм), Yb/Er (0,97/1,56 мкм) и Tm (1,9 мкм) представлены в табл. 1.12 [420].
1.9. Проблемы и перспективы
Настоящая книга касается только некоторых проблем взаимодействия света с биологическими тканями, связанных в основном с рассеянием и поглощением света случайными и квазиупорядоченными структурами, а также переизлучением света компонентами биотканей. Рассмотренные в этой и последующих главах эффекты и результаты исследований показывают необходимость углубленного изучения оптики биотканей с разнообразной структурной организацией. К настоящему времени качественная (а иногда и количественная) картина распространения света в биотканях может быть описана достаточно полно, что позволяет реализовывать ту или иную стратегию оптической диагностики, терапевтического или хирургического воздействия. Однако в ряде случаев количественные оценки дозы облучения или диагностического параметра оказываются затруднительными из-за отсутствия надежных данных для оптических параметров биотканей или их изменения в процессе взаимодействия света с объектом.
Традиционные спектрофотометрические, угловые и поляризационные методы измерений оказываются полезными для изучения биотканей. Дальнейшее развитие этих методов в направлении биомедицинских приложений требует построения более совершенных моделей тканей, учитывающих пространственное распределение поглотителей и рассеивателей, их полидисперсность, оптическую активность и двулучепреломление материала рассеивателей и базового вещества.
Необходимо развивать методы решения обратных задач с учетом реальной геометрии образца и лазерного пучка, справедливые для произвольного отношения коэффициентов рассеяния и поглощения. Во многих случаях хорошие результаты дает инверсный метод Монте-Карло [12, 13, 30–32, 66, 426–429]; для быстрых расчетов, требующихся при реализации практических медицинских методик диагностики и дозиметрии, могут быть полезны методы, базирующиеся на приближенных решениях уравнений теории переноса излучения.
В настоящее время ведутся интенсивные исследования диффузных волн фотонной плотности, лежащих в основе модуляционных фазовых методов исследования оптических характеристик биотканей [1, 3, 12, 13, 30–32, 162, 163], однако проблема
1.9. Проблемы и перспективы |
93 |
требует дальнейшей разработки в плане создания надежных алгоритмов восстановления 3-мерных изображений биотканей и построения оптических томографов.
Метод матрицы рассеяния хорошо известен в оптике и в последнее время используется многими авторами для исследований биотканей и клеточных суспензий. Обычно анализируется матрица интенсивности (матрица Мюллера), между тем, применение двухчастотных лазеров, таких как зеемановский лазер, или оптического когерентного томографа (ОКТ) позволяет измерять элементы амплитудной матрицы (матрицы Джонса), что открывает путь для упрощения решения обратной задачи для многих биологических структур [27, 32, 76, 123].
Дозиметрия лазерного излучения — очень важное направление исследований в фотобиологии, необходимое для практической реализации многих методов фототерапии. К настоящему времени многими авторами разработаны основные дозиметрические принципы [2, 3, 12, 13, 30–32, 62, 210, 211]. Тем не менее, необходимо развивать 3-мерные дозиметрические модели, учитывающие индивидуальные особенности биотканей, технологию фототерапии и оптические характеристики терапевтических устройств.
Когерентно-оптические методы исследования биотканей, основанные на эффектах дифракции, интерференции, фазовой, конфокальной и голографической микроскопии, представляют значительный интерес для развития фотомедицины [1, 3, 5, 10, 12–41, 103–106, 111–125, 146, 397, 430–446]. Для лазерной диагностики неоднородных тканей перспективными являются методы спекл-оптики и спекл-ин- терферометрии [5, 9–13, 19, 27, 31, 41, 101, 104, 105, 121, 128, 175, 176, 400–407]. Много полезной информации о когерентных методах исследования и их приложениях в оптике клеток и биотканей можно найти в обзорах [172, 392]. В частности, в [392] рассмотрены физические основы клеточного движения и лазерная доплеровская анемометрия как основной метод бесконтактного мониторинга клеточного и внутриклеточного движения, что очень важно при исследованиях биотканей in vivo.
Затрагиваемые в настоящей книге вопросы поляризационных свойств биотканей имеют прямое отношение к поляризационной физиологической оптике, основные идеи которой изложены в обзоре [447].
Г л а в а 2
РАСПРОСТРАНЕНИЕ СВЕТА В БИОЛОГИЧЕСКИХ ТКАНЯХ
2.1. Распространение непрерывного излучения
Основные закономерности распространения света в биологических тканях могут быть описаны на основе представлений о переносе излучения в случайно-неодно- родных средах. Известны два подхода к такому описанию — это теория переноса излучения, характеризующая эволюцию распространяющегося в среде потока энергии излучения, и теория многократного рассеяния, описывающая волновые свойства рассеянных световых полей (см. [120, 245]). В отличие от теории многократного рассеяния, теория переноса излучения не позволяет описать эффекты интерференции волн при рассеянии когерентного излучения; однако между двумя подходами существует фундаментальная взаимосвязь, определяемая соотношением между угловым спектром потока излучения, получаемым в рамках теории переноса, и пространственной корреляционной функцией флуктуаций рассеянного поля, получаемой в теории многократного рассеяния.
Подобная взаимосвязь позволяет ввести такую универсальную характеристику для описания распространения света в случайно-неоднородной среде, как плотность распределения оптических путей составляющих рассеянного поля ρ(s). Универсальность заключается в возможности получения параметров рассеянного поля как интегральных преобразований ρ(s) с соответствующим образом выбранными ядрами, в то время как функция ρ(s) может быть получена в рамках теории переноса излучения.
Итак, достаточно строгое математическое описание процесса распространения непрерывного излучения (немодулированного по интенсивности света) в рассеивающей среде может быть сделано с помощью стационарной теории переноса излучения (ТПИ). Теория переноса справедлива для ансамбля достаточно удаленных друг от друга рассеивателей и с успехом применяется при решении ряда практических задач из оптики биотканей. Основное стационарное уравнение ТПИ для монохроматического света имеет вид [1, 3, 12, 13, 18, 27, 30–32, 245, 448]
|
|
∂I(r, s) |
|
µs |
|
′ |
′ |
′ |
|
|
|
|
|
|
= −µtI(r, s) + |
|
|
I(r, |
s )p(s, s )dΩ |
, |
(2.1) |
||
|
|
∂s |
4π |
||||||||
|
|
|
|
|
4π |
|
|
|
|
|
|
где I |
′(r, s) — лучевая интенсивность в точке′ |
r в |
направлении |
s, Вт · м−2 · ср−1; |
|||||||
p(s, s ) — фазовая функция рассеяния; dΩ |
— единичный телесный угол в направле- |
||||||||||
нии s′; µs/µt ≡ Λ — альбедо единичного рассеивателя. Предполагается, что внутри cреды отсутствуют источники излучения. При наличии источника в среде в правую часть необходимо добавить член, характеризующий функцию источника S(r, s).
Если процесс переноса излучения исследуется в области G R3, а ∂G — граница области, то граничные условия на ∂G могут быть записаны в общем виде [449]:
I(r, s)|(sn)<0 |
= S(r, s) + RI(r, s) (sn)>0 , |
(2.2) |
|
|
b |
|
|
|
|
|
|

2.1. Распространение непрерывного излучения |
95 |
где r ∂G; n — внешняя нормаль к ∂G; S(r, s) — лучевая интенсивность падающего
света, b — оператор отражения.
R
При наличии в области G отражающих или преломляющих свет поверхностей условия, аналогичные (2.2), должны быть заданы на каждой из них.
Практический интерес, как правило, представляет не сама функция I(r, s), а интегралы от нее по некоторым областям фазового пространства (r, s). Например, при оптическом зондировании биотканей измеряемой величиной часто является функция распределения выходящего излучения на поверхности cреды:
Φ(r) = |
I(r, s)(sn)dΩ, |
(2.3) |
|
(sn)>0 |
|
где r ∂G.
В задачах дозиметрии оптического излучения в биотканях такой величиной яв-
ляется полная освещенность в точке: |
|
U (r) = I(r, s)dΩ. |
(2.4) |
4π
Фазовая функция p(s, s′) описывает рассеивающие свойства среды и представляет собой функцию плотности вероятности для рассеяния в направлении s′ фотона, движущегося в направлении s, т. е. характеризует элементарный акт рассеяния. Если рассеяние симметрично относительно направления падающей волны, тогда фазовая функция зависит только от угла ϑ между направлениями s и s′, т. е. p(s, s′) = p(ϑ).
Предположение о случайном распределении рассеивателей в среде, что означает отсутствие в структуре биоткани пространственной корреляции, ведет к следующей
нормировке:
π
p(ϑ)2π sin ϑ dϑ = 1.
0
Во многих практических случаях фазовая функция хорошо аппроксимируется с помощью постулированной функции Хеньи–Гринштейна [1, 3, 12, 13, 30–32, 171]:
p(ϑ) = |
1 |
· |
1 − g2 |
, |
(2.5) |
|
4π |
||||||
|
(1 + g2 − 2g cos ϑ)3/2 |
|
|
ϑ — угол рассеяния; g — средний косинус угла рассеяния (параметр анизотропии рассеяния) (см. (1.11)). Значение g изменяется в пределах от 0 до 1: g = 0 соответствует случаю изотропного (рэлеевского) рассеяния, g = 1 — полному рассеянию вперед (рассеянию Ми на крупных частицах [171]).
Интегродифференциальное уравнение (2.1) является сложным для анализа распространения света в рассеивающих средах, поэтому часто оно упрощается путем представления решения в виде сферических гармоник. Такое упрощение приводит к системе из (N + 1)2 связанных дифференциальных уравнений в частных производных, известной как PN -приближение. Эта система уравнений может быть сведена к одному дифференциальному уравнению (N + 1)-го порядка. Например, для N = 1 необходимы четыре связанных дифференциальных уравнения, которые сводятся к единственному уравнению диффузионного типа [1, 3, 12, 13, 30–32, 450–456]. Для изотропной среды оно соответствует случаю, когда направленной составляющей

96 Гл. 2. Распространение света в биологических тканях
лучевой интенсивности в уравнении (2.1) можно пренебречь по сравнению с изотропной составляющей, и имеет следующий вид:
( 2 − µd2)U (r) = −Q(r), |
(2.6) |
где |
|
µd = {3µa(µa + µs′)}0,5 |
(2.7) |
— диффузионный коэффициент (или эффективный коэффициент ослабления); |
|
Q(r) = D−1 · Sd(r), |
|
Sd(r) — функция источника диффузного излучения, т. е. число фотонов, инжектиру- |
|||
емых в единицу объема; |
|
+ µ′)]−1 |
|
D = c[3(µ |
a |
(2.8) |
|
|
s |
|
|
— коэффициент диффузии фотонов; |
|
|
|
µs′ = (1 − g)µs |
(2.9) |
||
— приведенный (или транспортный) коэффициент рассеяния; c — скорость света в среде.
Средняя транспортная длина пробега фотона определяется выражением
|
|
l |
tr |
= (µ |
+ µ′)−1 |
, |
(2.10) |
|
|
|
a |
s |
|
|
|
где µ |
= (µ + µ′) — транспортный коэффициент. |
|
|
||||
tr |
a |
s |
|
|
|
|
|
Отметим важное обстоятельство, что средняя транспортная длина пробега фотона
в среде с анизотропным однократным рассеянием существенно выше длины свободного пробега в среде с изотропным однократным рассеянием: ltr lph, lph
(см. (1.1)). Транспортная длина ltr означает такую длину, на которой фотон полностью теряет свое первоначальное направление.
Диффузионная теория оказывается хорошим приближением в случае малых значений фактора анизотропии однократного рассеяния (g 6 0,1) и больших альбедо (Λ → 1). Для большинства биотканей g ≈ 0,6–0,9, а для крови даже может дости-
гать 0,995 [12, 13, 31], что существенно ограничивает применимость диффузионного
s
приближения. Считается, что при оптических толщинах объекта, τ = µt ds = 10–20,
0
диффузионное приближение можно использовать при g < 0,9. Диффузионное приближение оказывается также неприменимым вблизи поверхности объекта на входе светового пучка, где преобладает однократное или малократное рассеяние. В этом случае условие применимости диффузионного приближения к описанию распределения интенсивности рассеянного излучения в случайно-неоднородной (рассеивающей) среде может быть сформулировано как rsd l = (µ′s)−1, где rsd — расстояние между источником и приемником. Параметр l , близкий по своему значению транспортной длине ltr, для µs µa, играет важную роль в описании переноса излучения в случай- но-неоднородных средах, определяя характерное расстояние распространения света в среде, на котором направленный поток излучения преобразуется в диффузный. Другим условием применимости диффузионного приближения является малое поглощение рассеивающей среды, что выражается условием µ′s µa.
При нарушении данных условий (например, в случае детектирования рассеянного излучения вблизи источников или излучения, прошедшего через тонкий рассеивающий слой с анизотропным рассеянием, g 6 1) диффузионное приближение приводит к существенным расхождениям с экспериментальными данными или с результатами
2.1. Распространение непрерывного излучения |
97 |
моделирования по методу Монте-Карло (имеет место «кризис диффузионного приближения» [120, 454]).
Несмотря на эти ограничения, диффузионное приближение применимо к решению ряда задач при описании распространения света в биологических тканях, в том числе в диффузионной оптической томографии (ДОТ), что позволяет использовать аппарат решения краевых задач диффузии. Решение уравнения диффузии (2.6) для сред с ограниченной геометрией требует задания граничных условий и функции источника, исходя из следующих ограничений [120].
1. При зондировании среды направленным пучком излучения источник диффузной составляющей локализован не на поверхности среды, а на некоторой глубине z0 l = (µ′s)−1, поскольку преобразование направленной составляющей в диффузную осуществляется на глубине порядка l . Таким образом, в простейшем случае изотропного точечного источника I0δ(r), погруженного в безграничную рассеивающую среду, функция источника должна быть введена не в форме I0δ(z)ϕ(x, y) (ось z перпендикулярна границе среды), а в форме I0δ(z − z0)ϕ(x, y). Возможно также использование не локализованного, а экспоненциально распределенного по глубине источника, что соответствует преобразованию в поверхностном слое направленной составляющей в диффузную.
2. Граничное условие для классической диффузионной задачи записывается в форме U (r)|r=∂G = 0 (где ∂G — поверхность, ограничивающая область пространства, где происходит диффузия). Применительно к описанию диффузии излучения это условие должно быть модифицировано для учета влияния отражения света на границе. Например, при диффузии света в полубесконечной среде, что представляет интерес с точки зрения диагностических приложений, когда осуществляется детектирование обратно рассеянного излучения, такая модификация приводит к граничному условию в форме U (r)|z=−zp = 0 (где zp — длина экстраполяции). То есть интенсив-
ность диффузной составляющей обращается в 0 не на геометрической границе, а на некоторой плоскости, параллельной границе и находящейся от нее на расстоянии zp. Отношение zp/l зависит от отражательной способности границы.
Решение задачи о диффузии излучения в ограниченных областях пространства может быть получено с помощью стандартной техники решения краевых задач; например, для областей в форме полупространства или слоя используется метод источников [504].
Важным является вопрос о влиянии поглощения на транспортные свойства рассеивающей среды. В диффузионной теории коэффициент диффузии излучения вводится в форме (2.8). Вместе с тем было показано (см. [31, 120]), что лучшее соответствие между экспериментом и диффузионной теорией достигается в случае, если D принимается равным D = c/3(1 − g)µs, т. е. не зависящим от коэффициента поглощения среды. Это позволяет проанализировать статистику оптических путей в случае поглощающей среды путем вычисления плотности вероятности ρ(s) для непоглощающей среды с заданными значениями µs и g, а затем учесть поглощение путем введения бугеровского множителя exp(−µas) в выражении для ρ(s).
Сделаем краткий обзор других решений транспортного уравнения. Если на оптически тонкую (τ < 1) поглощающую (альбедо Λ 0,5) биоткань падает плоская волна, интенсивность рассеянного поля оказывается много меньше интенсивности проходящей (когерентной) волны, которая описывается простым соотношением (1.1) или аналогичным [450]:
IT(s) = IT(0) exp(−τ ). |
(2.11) |
Это так называемое решение первого порядка. Если пучок узкий (например, лазерный), то такое приближение применимо и для более плотных (более рассеи-
4 Тучин

98 Гл. 2. Распространение света в биологических тканях
вающих) тканей (τ > 1, Λ < 0,9). Однако для некоторых тканей в области длин волн терапевтического/диагностического окна Λ ≈ 1, что делает неприменимым приближение первого порядка даже при τ 1.
Более строгое решение уравнения переноса можно получить методом дискретных ординат (многопотоковая теория), когда уравнение переноса (2.1) преобразуется в матричное дифференциальное уравнение для освещенности по многим дискретным направлениям (углам) [245]. При увеличении числа углов решение приближается
кточному. Возможно также раскладывать освещенность в ряд по сферическим гармоникам с разделением транспортного уравнения на компоненты для сферических гармоник. При достаточном числе сферических гармоник такой путь также ведет
кточному решению. Например, при исследовании биотканей в [457] использовалось до 150 сферических гармоник; полученные уравнения решались методом конечных разностей [458]. Однако при желании получить достаточно точное решение эти методы требуют объемных вычислений, они также плохо «работают» для δ-образных фазовых функций рассеяния [450].
Воптике биотканей широкое применение нашли более простые методы решения уравнения переноса, такие как двухпотоковая модель Кубелки–Мунка, трех-, четырех- и семипотоковые модели. Это эквивалентно представлению многих потоков по методу дискретных ординат только двумя (одномерная задача) или шестью (трехмерная задача) диффузными потоками. Такое представление естественно и весьма плодотворно при лазерном зондировании биоткани. Так, например, четырехпотоковая модель [245, 426] представляет собой два диффузных потока, распространяющихся навстречу друг другу (модель Кубелки–Мунка), и два коллимированных лазерных пучка — один падающий, а другой отраженный от задней границы образца. Очевидно, что в модели направление диффузных потоков выбирается совпадающим с соответствующими направлениями лазерных пучков. Семипотоковая модель — это простейшее трехмерное представление рассеянного излучения и падающего лазерного пучка в полубесконечной среде [89]. Конечно, простота и возможность очень быстрых расчетов дозы облучения или быстрого определения оптических параметров биоткани (решение обратной задачи рассеяния) даются ценой снижения точности.
Требуемая на практике надежная послойная дозиметрия лазерного излучения внутри биоткани, проблемы оптической диффузионной томографии и спектроскопии биообъектов определяют необходимость развития методов решения задач теории переноса излучения для сред с произвольной конфигурацией и любыми граничными условиями. Для решения таких задач перспективен метод Монте-Карло, широко применяемый для численного решения уравнения ТПИ [459, 460] в различных областях знаний (астрофизике, оптике атмосферы и океана и др.). В последние годы успешно развиваются приложения метода Монте-Карло в оптике биотканей [1–3, 12, 13, 27, 30–32, 74, 426–429, 461–476]. Метод Монте-Карло базируется на численном моделировании транспорта фотонов в рассеивающей среде. Случайное блуждание фотонов внутри образца биоткани прослеживается от точки влета в образец до его поглощения или выхода из образца.
Распределение интенсивности внутри биоткани является функцией коэффициента
поглощения µa, коэффициента рассеяния µs, параметра анизотропии g, а также размеров лазерного пучка. Это приводит к значительным трудностям в количественной дозиметрии излучения при лазерной терапии. Исследования распределения света внутри биоткани со сложной многослойной структурой с целью упрощения анализа могут быть проведены в рамках одномерной теории, которая справедлива, когда размеры лазерного пучка значительно больше глубины проникновения света в ткань, что реализуется для многих видов фототерапии. Типичными примерами многослойной биоткани являются кожа, стенки мочевого пузыря, матки, кровеносных сосудов.
2.1. Распространение непрерывного излучения |
99 |
Применение метода Монте-Карло базируется на использовании макроскопических оптических свойств среды, которые предполагаются однородными в пределах небольших объемов ткани. Моделирование не учитывает детали распространения энергии излучения внутри отдельной ячейки. Известные алгоритмы позволяют учесть несколько слоев биоткани с различными оптическими свойствами, конечный размер падающего пучка, отражение света от границ раздела слоев.
При высокой точности и универсальности главным недостатком метода МонтеКарло являются большие затраты машинного времени. Хотя развитие аппаратных и программных средств вычислительной техники уменьшает роль фактора времени, разработка новых средств 
 лазерной диагностики и терапии требует создания эф-
лазерной диагностики и терапии требует создания эф-
фективных, сравнительно простых и надежных алгоритмов метода Монте-Карло. Например, новый метод конденсированного Монте-Карло позволяет получить ре-
шение для любого значения альбедо (Λ = µs/µt) на основе моделирования для одного конкретного значения альбедо, что существенно ускоряет расчеты [427]. Разработаны также весьма экономные гибридные модели, сочетающие точность метода Монте-Карло и быстродействие диффузионных теорий или аппроксимирующих аналитических выражений [465, 466, 468].
Рассмотрим в качестве примера более подробно оп- |
|
|
|
|
|
|||
тику кожи человека [70, 71, 90, 426, 464, 471, 474–483]. |
|
|
|
|
|
|||
Для расчета распределений света Φ(r) и U (r) (см. (2.3) |
|
|
|
|
|
|||
и (2.4)) методом Монте-Карло рассмотрим кожу как |
|
|
|
|
|
|||
плоскую многослойную рассеивающую и поглощающую |
|
|
|
|
|
|||
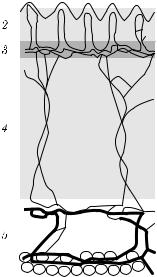
свет среду (рис. 2.1), на поверхность которой падает |
|
|
|
|
|
|||
лазерный пучок. При этом предполагается, что прост- |
|
|
|
|
|
|||
|
|
|
|
|
||||
ранственно-угловое распределение падающего излуче- |
|
|
|
|
|
|||
ния может быть представлено в виде |
|
Рис. 2.1. Модель кожи: 1 — |
||||||
|
S(r, s) = A(s)E(r), |
(2.12) |
эпидермис; 2 — папиллярная |
|||||
|
дерма; 3 — верхнее сплете- |
|||||||
где |
A(s) описывает угловое распределение источника |
ние микрососудов; 4 — ре- |
||||||
тикулярная дерма; 5 — глу- |
||||||||
единичной мощности. Каждый i-й слой характеризуется |
||||||||
бокое сосудистое сплетение |
||||||||
следующим набором параметров: µai, µsi, pi(ϑ), толщи- |
||||||||
[426] |
|
|
|
|||||
ной di и показателем преломления среды-наполните- |
|
|
|
|
|
|||
ля ni. |
к сдвигу |
плоскости, параллельной |
||||||
В |
силу симметрии задачи по отношению |
|||||||
поверхности раздела между слоями, а также благодаря радиальной симметрии падающего пучка света, функции U (ρ, z), ΦT(ρ), ΦR(ρ), определяющие соответственно распределение полной освещенности в среде и поверхностное распределение прошедшего и отраженного излучения, могут быть вычислены путем интегрирования [426, 464]:
|
∞ |
|
U (ρ, z) = |
G(ρ′, z)K(ρ, ρ′, ϕ) · ρ′ dρ′, |
(2.13) |
|
0 |
|
|
∞ |
|
ΦT, R(ρ) = |
GT, R(ρ′)K(ρ, ρ′, ϕ)ρ′ dρ′, |
(2.14) |
|
0 |
|
4*

100 Гл. 2. Распространение света в биологических тканях
где
2π
K(ρ, ρ′, ϕ) = E[(ρ′2 + ρ2 − 2ρρ′ cos ϕ)1/2]dϕ,
0
ρ, z, ϕ — цилиндрические координаты; ϕ — азимутальный угол в плоскости (x, y); G, GT и GR — функции Грина отклика среды на «точечное» внешнее воздействие, которые определяют соответственно распределение полной освещенности в среде и поверхностное распределение прошедшего и отраженного света.
Непосредственное статистическое моделирование движения фотонов осуществляется следующим образом. Вся область с отличной от нуля освещенностью разбивается на ячейки (i, j), каждый фотон характеризуется тремя координатами и двумя углами, определяющими направление его движения. При инициализации фотон помещается в начало координат, ему придается начальный вес W0, а его случайное направление определяется в соответствии с функцией A(s) по формуле
xrnd
a = |
p(x)dx, |
(2.15) |
xmin
где a — случайное число, равномерно распределенное в интервале [0, 1]; p(x) — функция плотности вероятности случайной величины x; xmin — минимальное значение x, xrnd — выбираемое значение x. Значения всех других случайных величин, необходимых для моделирования, также генерируются с помощью формулы (2.15) [459, 460].
После определения направления движения фотона вычисляется длина пробега фотона на данном шаге моделирования, которая учитывает процесс отражения или преломления на границе слоев (по формулам Френеля). Далее часть веса фотона, пропорциональная (1 − Λ) = µa/µt, записывается в ячейку Qij , характеризующую распределение поглощенной энергии в среде. Значения индексов i, j вычисляются по текущим координатам фотона. Затем генерируется новое значение угла рассеяния фотона, и процедура повторяется. Когда вес фотона уменьшается до заданного малого значения, выполняется процедура «рулетки». Если на очередном шаге моделирования фотон попадает за пределы среды, то часть его веса, пропорциональная коэффициенту пропускания соответствующей границы, записывается в ячейку массива QTi (пропускание) или QRi (отражение). Значение индекса i определяется текущей координатой ρ.
После того как описанная процедура выполнена для достаточно большого числа фотонов Np (обычно 105–107 в зависимости от решаемой задачи и сложности геометрии объекта), функции Грина отклика среды вычисляются по формулам:
Gij = |
Qij |
|
, |
(2.16) |
||
NpVij |
|
|
||||
|
µaij W0 |
|
||||
Gli = |
Qli |
|
, l = R, T , |
(2.17) |
||
NpSiW0 |
||||||
|
|
|
|
|||
где Vij — объем ячейки (i, j); µaij — коэффициент поглощения слоя, которому
принадлежит ячейка (i, j); Si |
— площадь кольца, соответствующего расстоянию ρ. |
|||||||
Окончательно по заданному профилю падающего пучка мощности P и радиуса r0, |
||||||||
который может быть гауссовым |
πr02 |
h− r0 |
i |
|
||||
|
g |
|
||||||
|
|
2P |
|
|
ρ |
2 |
|
|
E (ρ) = |
exp |
2 |
, |
(2.18) |
||||
|
|
|||||||
2.1. Распространение непрерывного излучения |
101 |
|
или прямоугольным |
|
|
0, |
ρ > r0, |
|
Ef(ρ) = P/(πr02), |
ρ 6 r0 |
(2.19) |
с помощью формул (2.13), (2.14) вычисляются распределение освещенности внутри среды и распределение прошедшего и отраженного излучения.
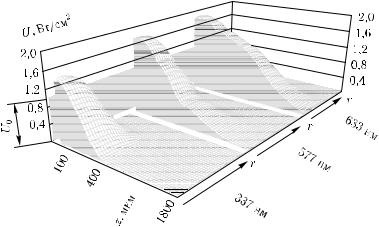
В качестве примера использования алгоритма на рис. 2.2, 2.3 представлены результаты численного моделирования распределения интенсивности для пучков гауссова профиля в коже (см. рис. 2.1 и табл. 2.1) [426, 464, 481–483]. Рис. 2.2 показывает распределение полной освещенности для трех длин волн (337, 577 и 633 нм), рис. 2.3 иллюстрирует зависимость освещенности в точке максимума Um
и размеров области максимальной освещенности Dm (определяемой по уровню 1/e2) от радиуса падающего пучка для длины волны 633 нм. Видно, что максимум освещенности формируется на некоторой глубине внутри ткани, а полная освещенность в точке максимума Um может значительно превышать освещенность U0 в центре падающего на поверхность среды пучка. Это обстоятельство неоднократно отмечалось исследователями (см., например, [1, 3]), причем отношение Um/U0 сильно зависит от оптических параметров cреды, радиуса падающего пучка и свойств границы [210, 211].
Рис. 2.2. Теоретические распределения интенсивности U в коже при ее облучении лазерными пучками разных длин волн (интенсивности в центре (U0 = 1 Вт/см2) и радиусы гауссовых пучков (r0 = 1 мм) на поверхности кожи одинаковы для всех лазеров), полученные методом Монте-Карло
Ослабление широкого пучка с падающей интенсивностью I0 в условиях многократного рассеяния может быть приближенно описано с помощью простого соотношения, близкого по форме к (1.1):
I(z) = I0q · exp(−µdz), |
(2.20) |
где q учитывает не только отражение света на границе раздела воздух–поверхность биоткани, тип используемого детектора (изотропного или анизотропного), но также и дополнительное увеличение освещенности верхних слоев биоткани за счет обратного рассеяния. Это приближенное соотношение справедливо лишь внутри биоткани, вдали от ее поверхности, на глубинах z > ld = µ−d 1. Типичные значения параметра q
