Борзенко,Зайцев

1 – δy = (G9 – G90)/G90; 2 – δlн = (lн – lн0)/lн0;

3 – δG = ( G – GL)/Gн0; 4 – δQн = (Qн – Qн0)/Qн0

После прекращения действия теплового импульса в структурных элементах низкотемпературной ступени охлаждения происходит постепенное восстановление параметров гелиевых потоков, причем скорость их изменения связана с инерционностью структурных элементов.

Из проведенного анализа следует, что импульсные тепловыделения объекта криостатирования при определенных условиях могут вызвать существенные количественные и качественные изменения параметров гелиевых потоков в нижней ступени охлаждения. Это существенным образом сказывается на параметрах работы криогенных машин и аппаратов ступеней предварительного охлаждения системы криогенного обеспечения сверхпроводящих машин и устройств.

52

4. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ФАЗОВОГО РАВНОВЕСИЯ КОМПОНЕНТОВ СМЕСИ

4.1. Термодинамические основы фазового равновесия растворов

Ваппаратах узлов низкотемпературной ректификации применяются двухфазные системы, состоящие из жидкой и паровой фаз и включающие два или более компонентов. На контактных устройствах осуществляется соприкосновение жидкой и паровой фаз,

ив результате тепло- и массообмена происходит непрерывный обмен веществом между фазами, стремящимися к равновесию.

Для определения условий фазового равновесия рассматривают закрытую систему, в которой осуществляется обмен веществом между фазами. В то же время каждая из фаз представляет собой открытую систему, так как является раствором с переменным составом [27].

Вслучае, когда жидкая фаза является идеальным раствором

и описывается законом Рауля, парциальное давление компонента в идеальном растворе pi = psi(T) xi, где psi(T) – давление насыщенного пара чистого компонента при температуре раствора Т; xi – молярная доля компонента в жидкой фазе.

При нахождении равновесных концентраций пара или жидкости часто используют константу фазового равновесия

где yi – молярная доля компонента в паровой фазе, а также коэффициент разделения

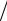Ki = psi (T ) p .

Для идеальных растворов с идеальной газовой смесью в паровой фазе при Т = const коэффициент разделения может быть найден из отношения парциальных давлений компонентов:

53

Температуру насыщения при фазовом переходе в идеальных

Если пар является неидеальной смесью, то для сохранения простой связи между изотермическими изменениями химического потенциала и мерой способности вещества переходить из одной системы в другую вводят величину f – летучесть, или фугитивность. В общем случае летучесть реального вещества является сложной функцией состояния от температуры и давления. Значение летучести приближается к величине давления при сближении свойств реального

При проведении исследований и решении практических задач удобно оперировать эталонными, или стандартными, состояниями, которые входят в определение «летучесть». Вводя понятие стандартного состояния (обозначено надстрочным индексом 0), получают для компонента смеси ai = fi 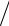fi0 . Это так называемая относительная летучесть, или активность, а величина, получившая название «коэффициент активности»,

54

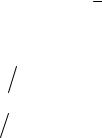
где δi – параметр растворимости компонента; δ – средневзвешенная растворимость смеси,

Еще более точные значения константы фазового равновесия могут быть получены по экспериментальным данным фазового равновесия бинарных и многокомпонентных систем.

4.2. Расчет фазового равновесия системы жидкость–пар бинарных и многокомпонентных смесей

В криогенной технике разделение смесей чаще всего осуществляют методом низкотемпературной ректификации в сочетании с другими процессами. Среди разделяемых смесей особый интерес представляют воздух, водород, природный газ.

Сухой и очищенный от углеводородных примесей атмосферный воздух представляет собой газовую смесь сложного состава.

Воздух – единственное исходное сырье для получения в промышленных масштабах кислорода, аргона, азота, неона, криптона, ксенона и др. (табл. 4.1).

Фракция низкокипящих компонентов, состоящая из гелия, водорода, неона, находится в ректификационной колонне в газообразном состоянии, накапливается с паром азота под крышкой конденсатора-испарителя нижней колонны, выводится из аппарата, и из нее методом низкотемпературной дефлегмации выделяется неон.

Криптон и ксенон имеют более высокую температуру кипения, чем остальные компоненты воздуха, поэтому они накапливаются в жидком кислороде и выделяются из него методом низкотемпературной ректификации в сочетании с другими методами. После обогащения криптоновый концентрат представляет собой бинарную смесь криптон–ксенон, которая разделяется методом

56

низкотемпературной ректификации.

57

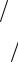
Бинарные и тройные смеси, состоящие из основных компонентов воздуха, в той или иной степени отклоняются от свойств идеальных газовых смесей и растворов, поэтому данные об их равновесных параметрах определяют в результате экспериментальных исследований. При обобщении опытных данных часто используют промежуточные функции γi, Ki [см. уравнения (4.6) и (4.7)], с помощью которых получают выражения, применяемые при расчетах на ЭВМ.

Для удобства обозначения состава бинарных и тройных смесей, состоящих из компонентов воздуха, принимаем, что индекс 1 относится к N2, 2 – к Аг, 3 – к O2, 4 – к Kr и 5 – к Хе.

4.2.1. Интерполяционные уравнения расчета равновесия тройной смеси азот–аргон–кислород

В работах [8, 13, 30] содержится обширная информация по равновесию системы азот–аргон–кислород, которая обобщена в виде интерполяционного уравнения для расчета фазового равновесия.

Однако более удобное обобщение данных по фазовому равновесию предложено В.С. Кортиковым и В.С. Суриной, которое приводится в работе [31]. При этом концентрацию в паре и жидкости тройной системы азот–аргон–кислород определяют по следующим выражениям:

для аргона

58

где

Свойства разделяемой смеси, наряду с другими параметрами, определяются закономерностью изменения фазового равновесия и коэффициентов разделения соответствующих бинарных систем. Константы фазового равновесия компонентов рассматриваемой тройной смеси азот–аргон–кислород изменяются по нелинейному закону (рис. 4.1).

59

Ki

Рис. 4.1. Изменение констант фазового равновесия компонентов смеси азот–аргон–кислород при x2 = 0,1 моль/моль:

1, 2, 3 – при p = 150 кПа; 1', 2', 3' – при р = 600 кПа

Наибольшие значения Ki (кривая 1) принадлежат легкокипящему азоту. Вместе с тем константы фазового равновесия компонентов системы азот–аргон–кислород имеют сложную зависимость от давления. Так, если при увеличении давления значения констант K3 и K2 увеличиваются, то K1 уменьшается. В рассмотренном диапазоне изменения концентраций и давлений коэффициенты разделения соответствующих бинарных смесей меняются незначительно. Например, при p = 150 кПа, x2 = 0,10 моль/моль и варьировании x1 от 0,05 до 0,90 моль/моль α12

изменяется от 2,391 до 2,163; α13 – от 3,438 до 3,245; α23 – от 1,438 до

1,500, а при р = 600 кПа при тех же значениях концентрации компонентов α12 изменяется от 1,926 до 1,922; α13 – от 2,348 до 2,563;

60

α23 – от 1,217 до 1,333.

4.2.2. Расчет фазового равновесия смесей кислород–криптон и криптон–ксенон

Криптон и ксенон являются наименее летучими компонентами воздуха, и температура кипения при стандартном давлении у криптона почти на 30 К, а у ксенона на 70 К выше температуры кипения кислорода. В связи с этим они накапливаются в жидком кислороде и представляют собой смесь кислород–(криптон + ксенон), относящуюся к разбавленным растворам, поскольку их суммарная объемная доля составляет 5·10–6.

Для расчета процесса ректификации на первом этапе выделения Kr и Xe важно знать зависимость для области малых содержаний примесей от исходной до 0,0001…0,001 объемной доли

Kr.

При расчете параметров фазового равновесия рассматриваемую смесь условно представляют бинарной (кислород– криптон), тогда концентрация криптона в паре

Сопоставление и обобщение опытных данных [32, 33] по фазовому равновесию смеси (3–4)* в области малых концентраций позволяет представить зависимость константы K4 от давления в виде

где р – давление, МПа; Т – температура, К.

Для расчета параметров фазового равновесия смеси кислород– криптон используем подпрограмму, текст которой на

* Здесь и далее даны обозначения соответствующих индексов компонентов смесей.

61