6.3.2. Способ концентрических сфер.

84. Построить линию пересечения тора с цилиндром вращения (рис. 179).

Рис. 179

Решение

Так как обе заданные поверхности являются поверхностями вращения, оси которых пересекаются в точке О (О₁, О₂) и параллельны фронтальной плоскости проекций, то применяем метод концентрических сфер. Приняв точку О₂ за центр сфер, описываем одну из них. Она пересекает обе поверхности по окружностям, фронтальные проекции которых есть отрезки А₂В₂, С₂Е₂ прямых. Точки I₂, II₂ пересечения этих отрезков будут принадлежать фронтальной проекции искомой линии пересечения. Горизонтальные проекции I₁, II₁ точек I и II находим обычным образом (задача I.2.3). Вспомогательные сферы проводим между максимальной и минимальной сферами. R_max равен отрезку О₂К₂. R_min равен наибольшему из перпендикуляров, опущенных из точки О₂ на очерковые образующие. Найдя достаточное количество точек, соединим их плавной лекальной кривой.

85. Построить проекции линии пересечения поверхностей (рис. 180 -189).

Рис. 180 Рис. 181

Рис. 182 Рис. 183

Рис. 184 Рис. 185

Рис. 186 Рис. 187

Рис. 188 Рис.189

6.3.3. Способ эксцентрических сфер.

86. Построить линию пересечения четверти кольца с конусом вращения (рис. 190).

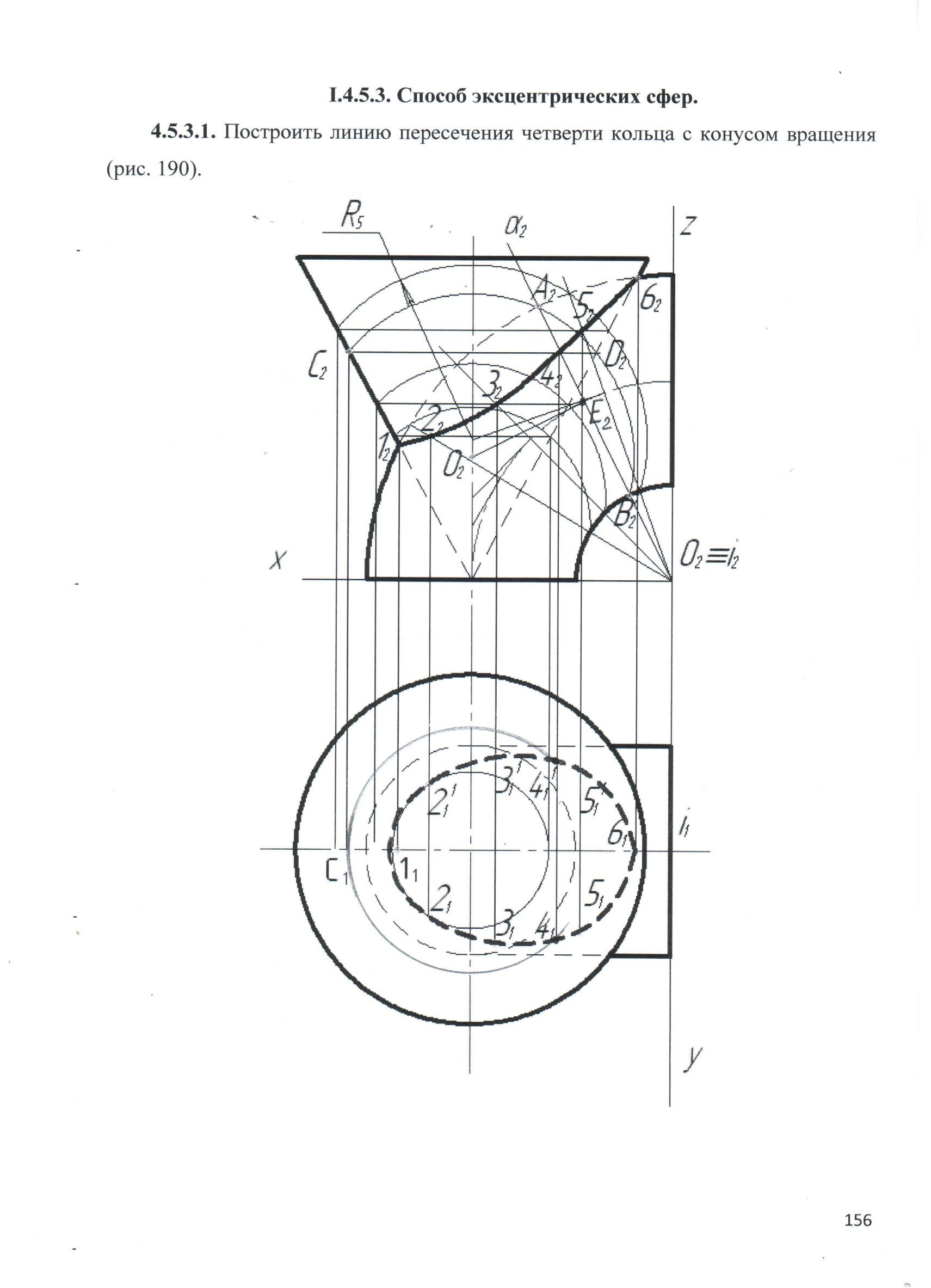
Рис. 190

Решение

Проведем через ось кольца i фронтально-проецирующую плоскость α (α₂). Она пересекает кольцо по окружности, фронтальная проекция которого есть отрезок А₂В₂ прямой. Множество центров сфер, пересекающих кольцо по этой окружности, будет лежать на перпендикуляре, восстановленном из точки Е₂ пересечения плоскости α₂ с линией центров круговых образующих. Точка пересечения О₂ этого перпендикуляра с осью конуса будет являться центром единственной сферы, которая пересечет кольцо по окружности А₂В₂, а конус - по окружности C₂D₂. Точка 4₂ пересечения фронтальных проекций этих окружностей и будет являться искомой точкой, принадлежащей линии пересечения. Её горизонтальная проекция строится обычным образом на окружности диаметром С₂D₂. Взяв как угодно много плоскостей α_i (α_2i) и производя аналогичные действия, получим достаточное количество точек, котoрые соединяем плавной лекальной кривой. Так как центры сфер каждый раз меняют своё положение на оси конуса вращения, то и метод называется методом эксцентрических сфер.

87. Построить проекции линий пересечения поверхностей (рис. 191 -200).

Рис. 191 Рис. 192

Рис. 193Рис. 194

Рис. 195Рис. 196

Рис. 197 Рис. 198

Рис. 199 Рис. 200

7. Метрические задачи

7.1. Определение натуральной величины отрезка прямой.

88. Найти натуральную величину отрезка прямой АВ и углы наклона прямой к плоскостям проекций П₁ и П₂ (рис. 201).

Рис. 201

Решение

Известно, что натуральная величина отрезка может быть определена как величина гипотенузы прямоугольного треугольника, одним катетом которого является проекция отрезка на плоскость проекций, а другим - разность расстояний концов отрезка до этой плоскости, т.е. разность высот или глубин, если рассматривать отрезок в системе двух плоскостей проекций (рис. 201).

Угол между горизонтальной проекцией А₁В₁ отрезка и гипотенузой является углом наклона α этой прямой к горизонтальной плоскости проекций. Угол  наклона прямой АВ к П₂ определяется как угол между А₂В₂ и гипотенузой прямоугольного треугольника А₂В₂А^-.

89. На прямой l от точки А отложить отрезок, равный h (рис. 202).

Рис. 202

Решение

На заданной прямой l берём произвольную точку B (B₁, B₂) и определяем истинную величину отрезка АВ. На гипотенузе А₁А^- построенного треугольника А₁В₁А^- откладываем отрезок A₁C^- = h. Из точки С^- проводим прямую, параллельную A^-B₁. Получаем точку C₁ и горизонтальную проекцию А₁С₁ искомого отрезка АС = h. По точке C₁ находим точку С₂. А₂С₂ - фронтальная проекция искомого отрезка АС.