3. Пересечение многогранника плоскостью.

Линия пересечения многогранника плоскостью представляет собой плоский многоугольник. Вершины этого многоугольника можно рассматривать как точки пересечения ребер многогранника с секущей плоскостью, а стороны – как линии пересечения граней многогранника с этой плоскостью.

Таким образом, различают два способа построения линий пересечения многогранника плоскостью: способ ребер и способ граней. При первом способе вершины многоугольника определяются многократным решением первой основной позиционной задачи, при втором способе – многократным решением второй основной позиционной задачи.

1. Плоскость проецирующая.

Если плоскость проецирующая, то задача решается очень просто, так как одна проекция линии пересечения вырождается в отрезок, а вторая проекция находится с помощью построения линий связи до пересечения с одноименными ребрами.

2. Плоскость общего положения.

Построить сечение пирамиды плоскостью, заданной двумя параллельными прямыми (рис. 62).

Решение задачи сводится к нахождению точек пересечения К, Т, Q ребер SА, SB и SC пирамиды SABC с плоскостью общего положения α (m n) путем многократного решения первой основной позиционной задачи. Видимость ребер пирамиды и плоскости определяется методом конкурирующих точек.

Рис. 62

4. Пересечение прямой с поверхностью многогранника.

Точки пересечения прямой с поверхностью называют точками встречи. Построение точек встречи совпадают с алгоритмом решения первой основной позиционной задачи.

Задача. Построить точки пересечения прямой l с поверхностью призмы (рис. 63).

Рис. 63

Решение

Графический алгоритм состоит из следующих операций:

1. l Σ;

2. Σ АВСА’B’C’ = 1 – 2 – 3;

3. l 1 – 2 – 3 = I, II.

5. Взаимное пересечение многогранников.

Построим линию пересечения 2-х многогранников на примере двух призм АВСА’B’C’ и DEFD’E’F’ (рис. 64).

Применим методику профессора Н.А. Рынина.

1. Определяем видимость проекций двух многогранников независимо от их расположения.

2. Определяем те ребра одного многогранника, которые заведомо не пересекаются с гранями другого, и наоборот, исходя из следующего: если хотя бы на одной из проекций ребра одного многогранника не пересекают грани другого, то и в пространстве они их не пересекают.

У призмы АВСА’B’C’ лишь ребро АА’ пересекает призму DEFD’E’F’. У второй призмы все три ребра DD’, EE’ и FF’ пересекают первую призму.

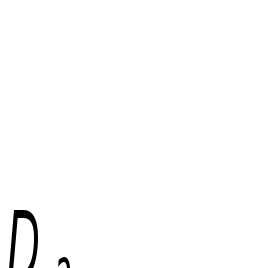
Рис. 64

3. Находим точки пересечения ребер одного многогранника с гранями другого, и наоборот.

4. Соединяем полученные точки, руководствуясь следующими правилами: две точки можно соединить между собой лишь в том случае, если они лежат в одной грани одного многогранника и в одной и той же грани другого.

5. Определяем видимость проекций двух многогранников в зависимости от их взаимного расположения.

7.6. Пересечение кривой поверхности плоскостью.

Линия пересечения кривой поверхности плоскостью есть плоская кривая линия. Она строится по отдельным точкам. Точки подразделяются на опорные и промежуточные.

К опорным относятся:

а) экстремальные точки, т.е. точки, находящиеся от плоскостей проекций на максимальном или минимальном расстояниях;

б) точки видимости, т.е. точки, которые отделяют видимую часть кривой от невидимой, Все остальные – промежуточные.

Рассмотрим примеры построения линии пересечения кривой поверхности плоскостью.

Пример №1.Построить линию пересечения поверхности вращения плоскостью частного положенияΣ(Σ₂).

В качестве поверхности вращения возьмем поверхность сферы, в качестве плоскости – фронтально-проецирующую плоскость (рис. 65).

Так как плоскость проецирующая, то фронтальная проекция линии пересечения представляет собой отрезок А₂В₂прямой линии.

Горизонтальная проекция линии пересечения строится по отдельным точкам из условия, что они лежат на поверхности сферы. Из опорных точек отметим точку видимости С₁ и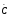 ₁. Они лежат на экваторе и поэтому будут отделять наП₁видимую часть кривой от невидимой. Случайные точкиD₁и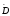₁ находятся обычным образом. Они лежат на параллели радиусаR.

Рис. 65

Пример №2.Построить линию пересечения конуса вращения плоскостью общего положения, заданной треугольникомАВС(рис. 66).

Чтобы свести построение линии пересечения к предыдущей задаче, применим способ преобразования комплексного чертежа, например, способ перемены плоскостей проекций и преобразуем всю систему так, чтобы плоскость общего положения стала бы проецирующей.

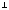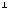Заменим П₂ наП₄ (АВС). У насАС– горизонталь, поэтому новая осьX₁₄ A₁C₁. Проекцией конуса наП₄будет также треугольник с вершинойS₄, проекцией плоскости – прямаяА₄В₄.

Рис. 66

Таким образом, задача свелась к предыдущему примеру. Проекцией линии пересечения на П₄будет отрезокМ₄Е₄.

Точки Е,МиN– опорные точки. ТочкаЕ– максимально удаленная точка отП₁,MиN – минимально удаленные точки, они лежат наП₁.

Вспомогательные точки на П₄ находятся обычным образом путем проведения горизонтальных плоскостей уровня. Фронтальные проекции точек наП₂находятся путем проведения из горизонтальных проекций точек линии связи и откладывания на них высот точек, снятых сП₄.