3. Варианты заданий вариант 1

Задача 1. Дискретная случайная величина X (CB X) задана рядом распределения:

xi	8	10	15	30	40
pi	0,1	0,2	0,3	0,1	0,3

Найти: 1) функцию распределения F(x); 2) числовые характеристики: математическое ожидание М(X), дисперсию D(X), среднее квадратическое отклонение (X), моду M₀(Х); 3) вероятность P(8 ≤ X < 30). Построить многоугольник распределения и график F(x).

Задача 2. Каждый из стрелков стреляет по мишени один раз. Вероятность того, что первый, второй и третий стрелки попадут в мишень при одном выстреле, соответственно равны 0,8; 0,6 и 0,9. Для CB Х – общего числа попаданий в мишень при указанных условиях, составить ряд распределения и найти F(x), M(X), (X) и D(X).

Задача 3. Вероятность появления некоторого события Ав каждом опыте равна 0,6. Требуется: 1) построить ряд распределения дискретнойCB X– числа появлений событияАв четырех независимых опытах; 2) оценить вероятность того, что в серии из 80 независимых опытов это событие появится не менее 60 раз.

Задача 4. Дискретная CB Xзадана рядом распределения:

xi	–2	–1	0	1	2	3	4
pi	0,05	0,10	0,15	?	0,15	0,20	0,10

Найти ряд распределения CB Y= –2X²+ 3,M(Y) иD(Y).

Задача 5. Непрерывная CB Xзадана функцией распределения

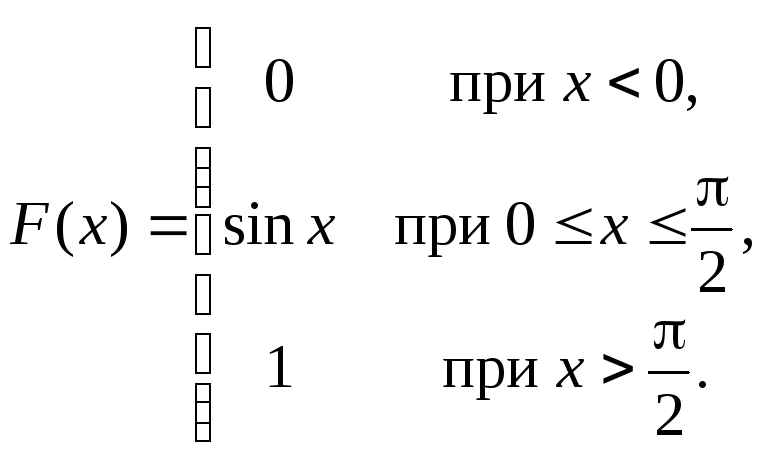
Найти: а) плотность распределения f(x); б)M(x); в)г) вероятность того, что в трех независимых испытанияхCB Xровно два раза примет значения, принадлежащие интервалу

Задача 6. Задана функция

Определить значение параметра A, при котором эта функция задает плотность распределения вероятности некоторой непрерывной CB X. Найти F(x), M(X) и D(X). Построить график F(x).

Задача 7. Заданы M(X) = 14 и(X) = 3 нормально распределенной непрерывнойСВ X. Найти:

1) вероятность ;

2) вероятность ;

3) симметричный относительно aинтервал, в который попадают значенияCB Хс вероятностью= 0,8385.

Задача 8. Шкала секундомера имеет цену деления 0,2 с. Отсчет времени делается с точностью до целого деления с округлением в ближайшую сторону. Ошибку отсчета при указанных условиях можно считать равномерно распределенной случайной величиной.

Найти вероятность произвести по этому секундомеру отсчет времени с ошибкой а) менее 0,05 с; б) не менее 0,01 с и не более 0,05 с.

Вариант 2

Задача 1. Дискретная случайная величина X(CB X) задана рядом распределения:

xi	–2	–1	2	5	7
pi	0,2	0,2	0,1	0,3	0,2

Найти: 1) функцию распределения F(x); 2) числовые характеристики: математическое ожидание М(X), дисперсию D(X), среднее квадратическое отклонение (X), моду M₀(Х); 3) вероятность P(–2 ≤ X < 5). Построить многоугольник распределения и график F(x).

Задача 2. В лотерее 100 билетов, из которых 10 выигрышных. Некто покупает 4 билета. Для СВ Х– числа выигрышных билетов среди тех, что будут куплены, составить ряд распределения и найтиF(x),М(X),(X).

Задача 3. Отчеты составляются независимо один от другого. Вероятность допустить ошибку при составлении каждого отчета равна 0,3. Требуется: 1) построить ряд распределения CB X –числа отчетов с ошибками среди четырех составляемых; вычислитьM(X),D(X) и(X); 2) оценить вероятность того, что при составлении 50 отчетов будет равно 20 отчетов с ошибками.

Задача 4. Известно, что дискретная CB X может принимать только два значенияx₁= –2 иx₂= 3 и ее математическое ожиданиеM(X) = 1,5. Составить ряды распределенияCB XиCB Z=НайтиF(z) и(Z).

Задача 5. Непрерывная CB Xзадана функцией распределения

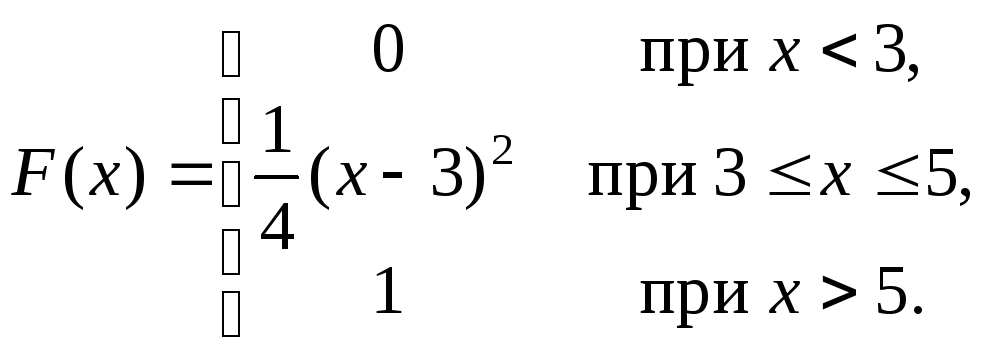
Найти: 1) плотность распределения f(x); 2)M(x) иD(X); 3)4) вероятность того, что в трех независимых испытанияхCB Xровно один раз примет значение, принадлежащее интервалу (1; 4).

Задача 6. Задана функция

Определить значение параметра A, при котором эта функция задает плотность распределения вероятности некоторой непрерывнойCB X. НайтиF(x),M(X),D(X). Построить графикF(x).

Задача 7. Заданы M(X) = 12 и(X) = 2 нормально распределенной непрерывнойСВ X. Найти:

1) вероятность ;

2) вероятность ;

3) симметричный относительно aинтервал, в который попадают значенияCB Хс вероятностью= 0,4515.

Задача 8. Случайная ошибка измерения некоторой детали подчинена нормальному закону с параметром = 20 мм. Найти вероятность того, что: а) измерение детали произведено с ошибкой, не превосходящей по модулю 22 мм; б) ни в одном из двух произведенных измерений ошибка не превысит по модулю 22 мм.