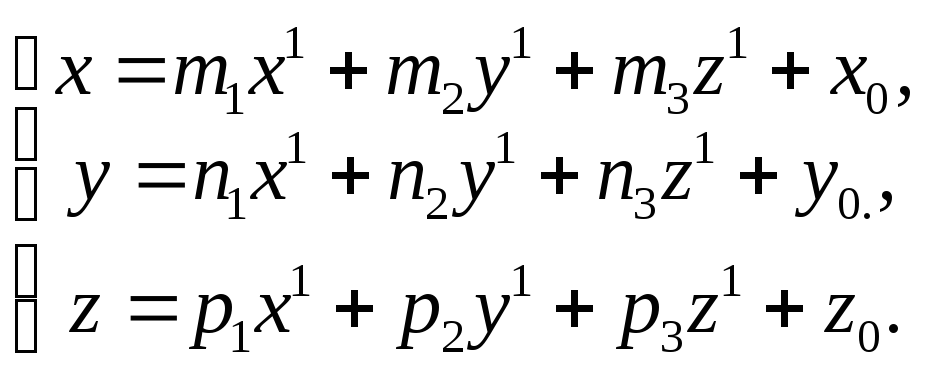- •Аналитическая геометрия
- •I. Элементы векторной алгебры
- •1.1. Геометрические векторы
- •1.2. Сложение векторов
- •1.3. Умножение вектора на действительное число
- •1.4. Коллинеарные векторы
- •1.5. Компланарные векторы
- •1.6. Проекция на прямую параллельно данной плоскости
- •1.7. Проекция вектора на ось
- •1.8. Ортогональная проекция вектора на ось
- •1.9. Скалярное произведение векторов
- •1.10. Векторное произведение векторов
- •1.15. Смешанное произведение векторов
- •II. Метод координат на плоскости и в пространстве
- •2.1 Введение системы аффинных и прямоугольных координат на плоскости и в пространстве
- •2.2. Аффинные задачи на плоскости и в пространстве
- •2.2.1. Координаты вектора, заданного координатами его концов.
- •2.3. Метрические задачи на плоскости и в пространстве .
- •2.3.1. Расстояние между точками.
- •2.3.2. Угол, заданный тремя точками.
- •2.4. Преобразование аффинных координат на плоскости и в пространстве
- •2.5. Преобразование прямоугольных координат на плоскости
- •2.6. Полярные координаты на плоскости
- •2.7. Цилиндрические и сферические координаты в пространстве
- •III. Образы первой ступени
- •3.1. Условия, определяющие фигуру в системе координат
- •3.2. Прямая в аффинной системе координат на плоскости и в пространстве
- •3.2.1. Уравнения прямой, проходящей через данную точку параллельно данному вектору
- •3.2.2. Уравнения прямой, проходящей через две точки
- •3.2.3. Общие уравнения прямой
- •I.Общее уравнение прямой на плоскости
- •2. Общие уравнения прямой в пространстве
- •3.2.4. Исследование взаимного расположения прямых
- •3.3. Прямая в прямоугольной системе координат на плоскости
- •3.3.1. Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору
- •3.3.2. Уравнение прямой, проходящей через данную точку под данным углом к оси (Ох)
- •3.3.3. Нормальное уравнение прямой
- •3.3.4. Угол между двумя прямыми, заданными общими уравнениями
- •3.3.5. Угол между наклонными прямыми, заданными уравнениями с угловыми коэффициентами
- •3.3.6. Расстояние от точки до прямой
- •3.4. Пучок прямых на плоскости
- •3.6. Прямая и плоскость в пространстве
- •3.6.1. Плоскость в аффинной системе координат
- •3.6.1.1. Уравнения плоскости, проходящей через данную точку параллельно двум данным векторам
- •3.6.1.2.. Уравнения плоскости, проходящей через три данные неколлинеарные точки
- •3.6.1.3. Общее уравнение плоскости
- •3.6.1.4. Исследование взаимного расположения двух плоскостей
- •3.6.2. Плоскость и прямая в прямоугольной системе координат
- •3.6.2.1. Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору
- •3.6.2.2. Угол между двумя плоскостями
- •3.6.2.3. Угол между прямой и плоскостью
- •3.6.2.4. Расстояние от точки до плоскости
- •3.6.2.5. Расстояние от точки до прямой
- •3.6.2.6. Расстояние между скрещивающимися прямыми
- •IV. Образы второго порядка
- •4.1. Элементарная теория линий второго порядка
- •4.1.1. Окружность
- •4.1.2. Эллипс
- •4.1.3. Гипербола
- •4.1.4. Парабола
- •4.1.5. Эллипс, гипербола и парабола в полярных координатах
- •4.2. Упрощение уравнения линии второго порядка
- •4.2.1. Преобразование уравнения линии второго порядка при повороте прямоугольной системы координат
- •4.2.2. Упрощение уравнения линии второго порядка. Метрическая классификация линий второго порядка
- •4.3. Поверхности
- •4.3.1. Цилиндрические поверхности
- •4.3.2. Конические поверхности
- •4.3.3. Поверхности вращения
- •4.3.4. Эллипсоид
- •4.3.5. Однополостный гиперболоид
- •4.3.6. Двуполостный гиперболоид
- •4.3.7. Эллиптический параболоид
- •4.3.8. Гиперболический параболоид
- •4.3.9. Прямолинейные образующие поверхности
- •V. Расширенные евклидовы плоскость и пространство
- •5.1. Определение расширенных евклидовых плоскости и пространства
- •5.2. Однородные координаты на расширенной евклидовой плоскости
- •5.3. Уравнения прямой, точки и линий второго порядка в однородных координатах на расширенной евклидовой плоскости
- •5.4. Однородные координаты в расширенном евклидовом пространстве
- •5.5. Уравнения плоскости и прямой в однородных координатах
- •Задачи по аналитической геометрии для домашних заданий
- •Метод координат на плоскости и в пространстве
- •Lll. Прямая линия на плоскости
- •LV. Плоскость и прямая в пространстве
- •V. Элементарная теория кривых второго порядка
- •Vl. Элементарная теория поверхностей
- •Vll. Другие системы координат на плоскости и в пространстве
- •Основная литература
2.2. Аффинные задачи на плоскости и в пространстве
2.2.1. Координаты вектора, заданного координатами его концов.
|
На плоскости
Дано: R
=
Найти координаты
вектора
Рис. 22
Решение.
А(х1,
у1)
В(х2,
у2)
Так
как
|
В пространстве
Дано: R
=
Найти координаты
вектора
Рис. 221
Решение.
А(х1,
у1,
z1)
В(х2,
у2,
z2)
Так
как
|
2. 2.2. Координаты точки, делящей отрезок в данном отношении.
Пусть даны
координаты двух точек А
и В.
Найдём координаты такой точки С,
что
![]() ().
().
Замечание. Из условия () следует, что точки А, В, С лежат на одной прямой. Если 0, то точка С лежит между точками А и В. Если 0, но 1, то точка С лежит вне отрезка АВ со стороны точки В. Если 0, но 1, то точка С лежит вне отрезка АВ со стороны точки А.
|
Если = 1, то С – середина отрезка АВ. Очевидно, всегда 1. Решение. Приведём решение в случае плоскости. В случае пространства |
|
решение проведите самостоятельно.
Пусть С(х,
у, z).
Тогда
![]() ,
,![]() .
Перепишем равенство ()
в координатах. Получим
.
Перепишем равенство ()
в координатах. Получим
х
х1
= (х2
х), у
у1
= (у2
у).
Отсюда

2.3. Метрические задачи на плоскости и в пространстве .
Замечание. Метрические задачи можно решать в любой АСК, но рациональные вычислительные формулы получаются в ПДСК.
2.3.1. Расстояние между точками.
|
На плоскости
Дано:
Найти АВ. Решение.
АВ
=
|
В пространстве
Дано: Найти АВ.
Решение.
АВ
=
|
2.3.2. Угол, заданный тремя точками.
Приведём решение этой задачи в случае пространства. Для плоскости решение проведите самостоятельно.
|
Дано:
Решение.
|
2.4. Преобразование аффинных координат на плоскости и в пространстве
Пусть R
= {O,
B}
и R1
= {O1,
B1}
два аффинных репера, где В
и В1
соответствующие базисы. Пусть Т
– матрица перехода от базиса В
к базису В1
и (х0к)
– столбец координат точки О1
в репере R.
Пусть М
– произвольная точка, (хк)
и (х1к)
– столбцы её координат в реперах R
и R1
соответственно. Тогда столбец координат
вектора
![]() в базисеВ
будет (хк
х0к),
а в базисе В1
– (х1к).
Используя формулу связи координат
вектора в разных базисах, получим
в базисеВ
будет (хк
х0к),
а в базисе В1
– (х1к).
Используя формулу связи координат
вектора в разных базисах, получим
(хк х0к) = Т(хк1), или (хк) = Т(хк1) + (х0к).
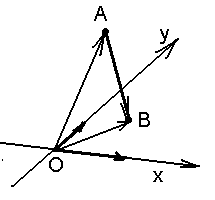
Если эту формулу переписать в координатах (на плоскости координаты точки обозначим х, у, в пространстве х, у, z) , получим
|
на плоскости
|
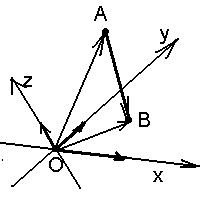
в пространстве
|
Так как матрица перехода всегда невырожденная, то определители этих формул отличны от нуля. Обратно, формулы () или () с определителем отличным от нуля всегда задают преобразование аффинных координат.
Задача 12. В
параллелепипеде АВСDA1B1C1D1
точки М, Р, К
заданы
равенствами
![]() ,
,![]() ,
,![]() .
Запишите формулы преобразования
координат, если системы координат
заданы
.
Запишите формулы преобразования
координат, если системы координат
заданы
|
заданы реперами
R
= {A,
Решение.
Для решения
первой части задачи нужно найти
«старые» координаты точки М
и векторов
|
Рис. 23 |
координатных векторов:
![]() ,
,
![]() ,
,![]() .
Получим следующие формулы преобразования
координат
.
Получим следующие формулы преобразования
координат

«Новые» координаты
точки К равны
(0, 0, 1). Подставив их в полученные формулы
вместо х1,
у1,
z1,
получим х =
0, у
=
![]() ,
z
=
,
z
=![]() .
Итак, «старые» координаты точки К
равны (0,
.
Итак, «старые» координаты точки К
равны (0,
![]() ,
,
![]() ).
«Старые» координаты точки В(0,
1, 0). Подставив их в найденные формулы
вместо x,
y,
z,
получим «новые» координаты x1
=
).
«Старые» координаты точки В(0,
1, 0). Подставив их в найденные формулы
вместо x,
y,
z,
получим «новые» координаты x1
=
![]() ,
у1
=
,
у1
=
![]() ,
z1
=
,
z1
=
![]() .
.