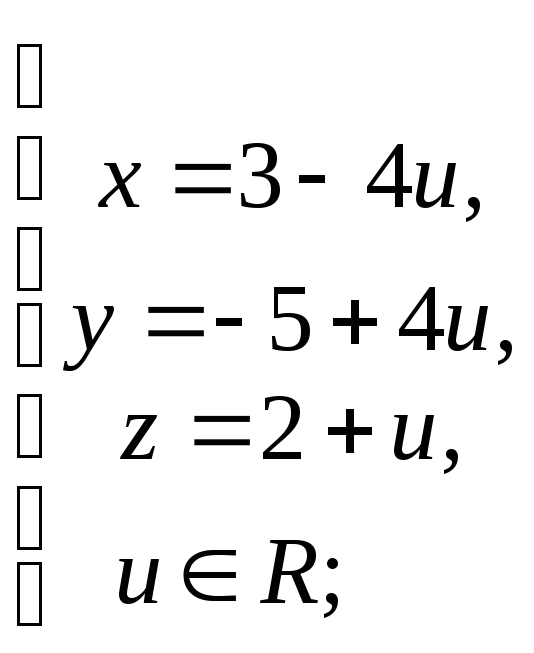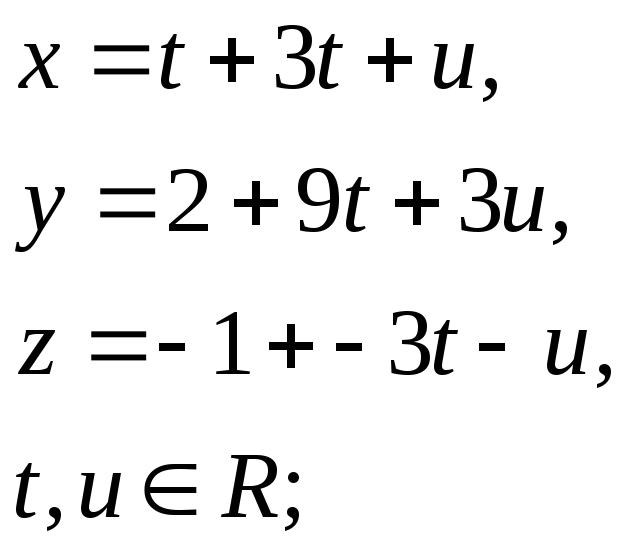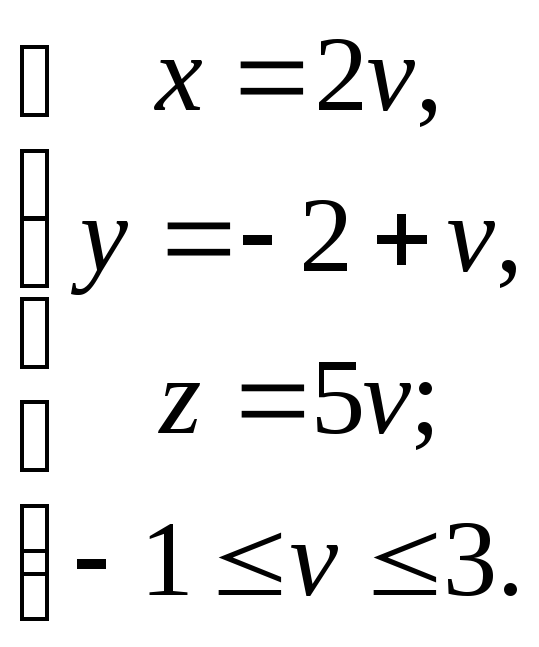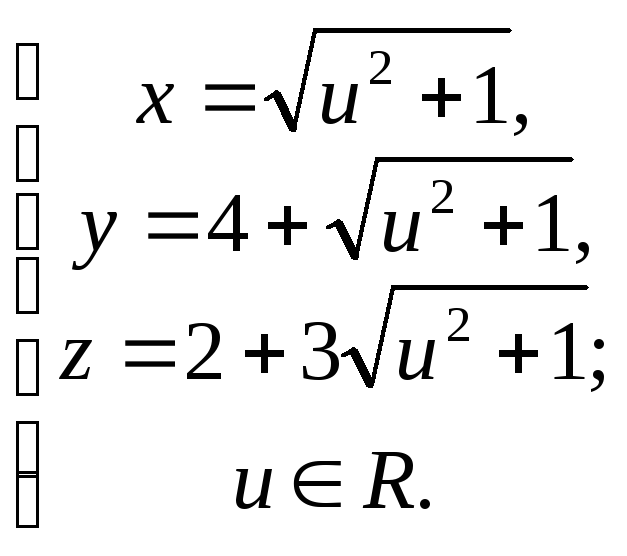5.4. Однородные координаты в расширенном евклидовом пространстве

Пусть в евклидовом пространстве до его расширения была введена системе аффинных координат с помощью репера . Выходя в четырёхмерное пространство, возьмём точкуS, не принадлежащую данному пространству и рассмотрим репер , где. Каждой точке расширенного пространства поставим в соответствие прямую, проходящую через эту точку и точкуS. Это соответствие будет взаимнооднозначным. Так как каждая проведённая прямая вполне определяется своим направляющим вектором, то между всеми точками пространства и всеми классами пропорциональных упорядоченных ненулевых четвёрок действительных чисел устанавливается тоже взаимнооднозначное соответствие

М  (X : Y : Z : T), где X, Y, Z, T не равны нулю одновременно.

Отношение (X : Y : Z : T) называется однородными координатами точки М и записывается М(X : Y : Z : T). Точка М будет собственной тогда и только тогда, когда T  0. Если (x, y, z) – соответствующие аффинные координаты этой точки, то ,,. Точка М будет несобственной тогда и только тогда, когда Т = 0. Следовательно, Т = 0 есть уравнение несобственной (бесконечно удалённой) плоскости.

5.5. Уравнения плоскости и прямой в однородных координатах

Если собственная плоскость П в аффинной системе координат была задана общим уравнениям Ax + By + Cz + D = 0, то в соответствующей однородной системе координат она будет иметь уравнение

AX + BY + CZ + DT = 0. (*)

Уравнение несобственной плоскости имеет такой же вид. Оно получается при А = В = С = 0, D  0. Итак, (*) всегда задаёт плоскость, если A, B, C, D не равны нулю одновременно. Это общее уравнение плоскости.

Пример 5. Точки M₁(X₁: Y₁: Z₁: T₁), M₂(X₂: Y₂: Z₂ : T₂), M₃(X₃: Y₃ : Z₃ :T₃) заданы однородными координатами и не лежат на одной прямой. Составьте уравнения проходящей через них плоскости.

Решение. Если ={X₁, Y₁, Z₁, T₁}, {X₂, Y₂, Z₂, T₂}, {X₃, Y₃, Z₃, T₃}, то векторы ,.линейно независимы и соответствуют точкамМ₁, М₂, М₃ соответственно. Точка М(X : Y : Z : T)  (М₁М₂М₃)  = {X, Y, Z, T} линейно выражается через векторы ,.. Отсюда получаем два вида уравнений искомой плоскости.

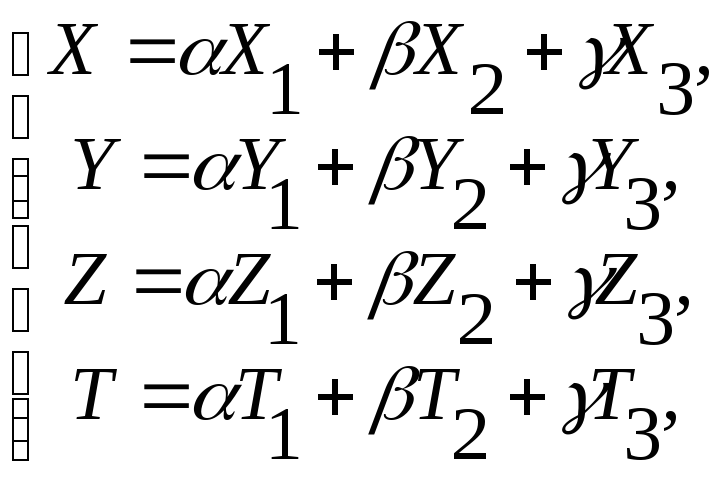где , ,   любые действительные числа. Это параметрические уравнения плоскости в однородных координатах.

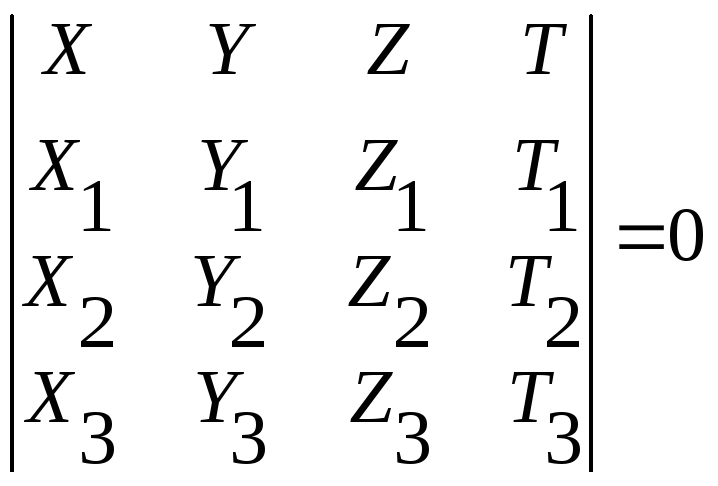
Используя другое необходимое и достаточное условие линейной зависимости векторов, получим

М(X : Y : Z : T)  (М₁М₂М₃)  .

Любую прямую можно задать как линию пересечения двух плоскостей и в расширенном пространстве любые две различные плоскости пересекаются, то любую прямую в однородных координатах можно задать системой уравнений ранга 2

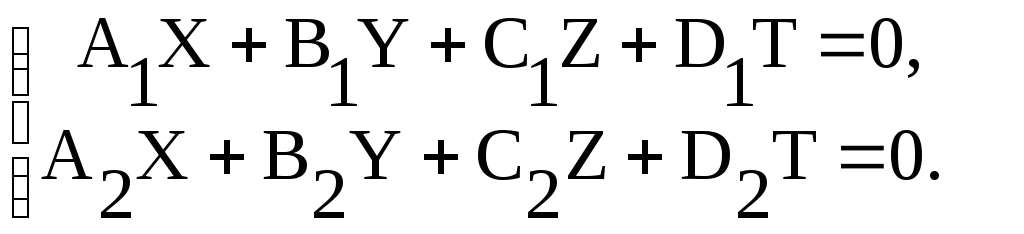
Это общие уравнения прямой в однородных координатах.

Пример 6. Запишите канонические уравнения эллипсоида, однополостного и двуполостного гиперболоидов, эллиптического и гиперболического параболоидов в однородных координатах.

Решение проведите самостоятельно и сравните полученные результаты.

Задачи по аналитической геометрии для домашних заданий

1. АВСDA₁B₁C_!D₁ – параллелепипед. Постройте точки, заданные равенствами ,,,,. Представьте векторнесколькими способами в виде а) суммы векторов, заданных построенными точками, б) линейной комбинации векторов, заданных построенными точками.

2. Даны две различные точки А и В. Постройте точки E, C, D, H, K, заданные равенствами . Выразите векторы,,,,,,,,через вектор.

3. ABCD – параллелограмм, = 4,N = (АD) Ç (BM), ,. Выразите векторы,,,,,через векторы и.

4. ABCD – тетраэдр, ,,,. Выразите векторы,,,,,,,через векторы,,(здесь О – точка пересечения медиан граниАВС).

5. ABCDEF – правильный шестиугольник, М и К – середины сторон AF и CD соответственно, О –центр шестиугольника, ,,,. Найдите матрицу перехода от базисае = к базисуе¹ = . Составьте формулы преобразования координат ри переходе оте к е¹. Используя «старые» координаты вектора , найдите его новые координаты. Используя «новые» координаты вектора, найдите его «старые» координаты.

6. ABCDA₁B₁C₁D₁ – куб с единичным ребром, К – середина диагонали АС, О = (АС)  (KD₁), ,,. Векторы,, единичные векторы, сонаправленные с векторами ,исоответственно. Найдите матрицу перехода от базисак базису {,,}. Используя «новые» координаты векторов,,, найдите их «старые» координаты.

7. В базисе даны векторыии. Найдите коэффициентыa, b, g так, чтобы .

8. Найдите коэффициенты a и b так, чтобы векторы ибыли коллинеарными.

9. Найдите коэффициент a так, чтобы векторы ,ибыли компланарными.

10. В базисе даны векторыи. Найдите,,и, если,,.

11. В базисе даны векторы,Найдите,,и, если,,,.

12. ABCDEF – правильный шестиугольник с единичной стороной, ,,. Найдитеи ортогональную проекцию векторана направление вектора. (Дайте векторное решение)

13. ABCDA₁B₁C₁D₁ – прямоугольный параллелепипед, |АВ| = 2, |ВС| = 4, |АА₁| = 5, ,,. Найдитеи ортогональную проекцию векторана направление вектора. (Дайте векторное решение)

14. Докажите векторным методом теорему о трёх перпендикулярах.

15. ABCDEF – правильный шестиугольник, . Найдите координаты вершин шестиугольника в системе координат, заданной репером, гдеО – центр шестиугольника, ,. Постройте точки с координатами (2, 1), (-1, 1), (2, -1), (-1,-1).

16. АВСDA₁B₁C_!D₁ – параллелепипед. Найдите координаты его вершин в системе координат, заданной репером , гдеО – центр параллелепипеда, ,,. Постройте точки с координатами (-0,5; 0; 0,5), (0; -1; 1), (1; 1; 1).

17. В условиях предыдущей задачи найдите координаты точек М, Р, К, если ,,.

18. В условиях задачи 5 заданы две системы аффинных координат реперами и. Запишите формулы преобразования координат. Запишите формулы преобразования координат.

19. В условиях задачи 6 две системы прямоугольных координат заданы реперами и.

20. ABCDEF – правильный шестиугольник, . Постройте точки, заданные координатами М(2; 2),N(-1; 1), P(1,5; -1,5) в системе координат, заданной репером , где О – центр шестиугольника,,. Найдите расстояния между этими точками,и площадь треугольника.

21. В кубе ABCDA₁B₁C₁D₁ с единичным ребром точки M, N, P, Q, Т заданы равенствами ,,,,,a Î R .

1) Используя только определение векторного произведения, найдите ,,.

2) Используя геометрический смысл модуля векторного произведения, найдите ,.

3) Введя ортонормированный базис, найдите ,.

4) Найдите площадь треугольника MPQ.

22. Упростите выражение .

23. Аффинная система координат задана репером , где,. Тетраэдр задан координатами своих вершинА(2, -3, 4), В(5, 1, 2), С(-3, 2,-3), D(4, -4, 5).

Найдите а) длины рёбер, б) величины плоских углов при вершине В, в) площадь грани АВС, г) объём тетраэдра, д) высоту, опущенную на грань АВС.

24. Векторы ,,заданы в ортонормированном базисе. Найдитеи,и. Сравните полученные результаты.

25. В параллелограмме ABCD точки М, N, P заданы равенствами ,,. Найдите площадь треугольникаMNP и длину его высоты, опущенной из вершины М, если ,,.

26. Векторы ,,заданы в базисе. Найдите, если,,. Определите ориентацию данной тройки векторов.

27. Найдите a и b так, чтобы векторы ,ибыли компланарными.

28. В прямоугольной системе координат заданы координаты вершин тетраэдра А(-1, 5, 2), В(3, 4, -1), С(4, 4, 5), D(3, -2, 8). Найдите объём тетраэдра, площадь грани АВС, длину высоты, опущенной из вершины D. Определите ориентацию тройки векторов ,,.

29. Заполните таблицу (система координат аффинная).

№	Данные, определяющие прямую	Чертёж	Парамет- рические уравнения	Канони- ческое уравнение	Общее уравнение
1	l ' A, l || , A(x0, y0),
2
3
4
5					Px + Qy + D = 0

30. Исследуйте взаимное расположение прямых, заданных в аффинной системе координат уравнениями:

1) 5х - 6у + 30 = 0; 2) ; 3)4), 5) 3х + 8у + 5 = 0.

31. Найдите уравнения всех сторон и диагоналей параллелограмма, если одна из его сторон лежит на прямой , одной из его вершин является точкаА(-1; 1) и точка К(4, 1) – его центр. Система координат аффинная.

32. Составьте уравнения сторон параллелограмма ABCD, зная, что его диагонали пересекаются в точке М(1, 6), а стороны АВ, ВС, CD и DА проходят соответственно через точки Р(3, 0), К(6, 6), Т(5, 9), Н(-5, 4). Система координат аффинная.

33. Прямая р проходит через точку Р(-3, -5) так, что отрезок, высекаемый на ней прямыми 2х + 3у - 15 = 0 и 4х - 5у - 12 = 0, делится точкой Р пополам. Найдите уравнение прямой р. Система координат аффинная.

34. Даны вершины треугольника А(4, 6), В(-4, 0), С(-1, -4). Составьте уравнение высоты, опущенной из вершины А на сторону ВС. Система координат прямоугольная.

35. Найдите точку, симметричную точке М(-2, 9) относительно прямой 2х - 3у + 18 = 0. Система координат прямоугольная.

36. Найдите координаты точки, лежащей на прямой х - 3у + 1 = 0 и равноудалённой от точек (-3, 1) и (5, 4). Система координат прямоугольная.

37. В DАВС известны уравнения стороны АВ: 4х + у - 12 = 0, высоты ВН: 5х - 4у - 15 = 0 и высоты АН: 2х + 2у - 9 = 0. Составьте уравнения двух других сторон и третьей высоты. Система координат прямоугольная.

38. Найдите косинус и тангенс угла между прямыми 2х + 5у - 3 = 0 и 5х + 2у + 6 = 0. Система координат прямоугольная.

39. Даны координаты вершин В(-2, 1) и С(4, 5) в основании равнобедренного треугольника и косинус угла при вершине А: . Найдите координаты вершиныА. Система координат прямоугольная.

40. Определите расстояния от точек (1, 0) и (-1, 2) до прямой 3х - у +4 = 0. Система координат прямоугольная.

41. Составьте уравнения прямых, отстоящих от прямой 5х + 12у + 1 = 0 на расстояние 5. Система координат прямоугольная.

42. Составьте уравнения биссектрис углов между прямыми иСистема координат прямоугольная.

43. Центр симметрии квадрата находится в точке (-1, 0), уравнение одной из его сторон х + 3у - 5 = 0. Составьте уравнения трёх других его сторон. Система координат прямоугольная.

44. Заполните таблицу (система координат аффинная).

№	Данные, определяющие плоскость	Чертёж	Парамет- рические уравнения	Уравнение с определи- телем	Общее уравнение
1	П ' М1, М2, М3, М1(2, -4, 0), М2(-7, 3, 5), М3(0, 5, 3).
2
3
4					5х - 3у + 15 = 0
5

45. Запишите общие уравнения плоскостей

1

2

46. Что задают следующие условия в системе аффинных координат?

47. Даны уравнения трёх граней параллелепипеда 2х + 3у + 4z - 12 = 0, x + 3y - 6 = 0, z + 5 = 0 и координаты (6, -5, 1) одной из его вершин. Составьте уравнения остальных трёх граней параллелепипеда. Система координат аффинная.

48. Найдите основание перпендикуляра, опущенного из точки (1, 3, 5) на прямую, по которой пересекаются плоскости 2x + y + z - 1 = 0 и 3x + y + 2z - 3 = 0. Система координат прямоугольная.

49. В прямоугольной системе координат заданы координаты вершин тетраэдра А(-1, 5, 2), В(3, 4, -1), С(4, 4, 5), D(3, -2, 8). Найдите длину высоты, опущенной из вершины D. Система координат прямоугольная.

50. Составьте уравнение плоскости, параллельной плоскости 2x + y - 4z + 5 = 0 и отстоящей от точки (1, 2, 0) на расстоянии . Система координат прямоугольная.

51. Что задают в аффинной системе координат следующие системы уравнений?

52. Составьте в АСК общее уравнение плоскости, проходящей через прямую и точкуМ₀ (-5, 4, 1).

53. Исследуйте взаимное расположение прямых, заданных в АСК уравнениями иЕсли прямые скрещиваются, то найдите уравнения плоскостей, каждая из которых проходит через одну из данных прямых параллельно второй прямой.

54. Найдите в ПДСК а) величину одного из углов между прямыми и, б) расстояние между этими прямыми, в) уравнение их общего перпендикуляра.

55. Составьте уравнение прямой, проходящей через точку (1, -3, 7) перпендикулярно плоскости 2x + y - 4z + 5 = 0. Система координат прямоугольная.

56. Найдите в АСК а) точку пересечения прямой и плоскости 2x + y - 4z + 5 = 0, б) угол между ними, если ,,,

57. Что задают в ПДСК на плоскости следующие уравнения

а) 4х² + 9у² - 36 = 0, б) 4х² + 9у² + 36 = 0, в) 4х² - 9у² - 36 = 0, в) 4х² - 9у² + 36 = 0, г) 4х + 9у² - 36 = 0, д) 4х² + 9у + 36 = 0,

е) 4х² + 8х + 9у² - 18у - 36 = 0, ж) 4х² + 8х - 9у² - 18у - 36 = 0, з) 4х + 9у² + 18у - 36 = 0? Найдите все характеристики этих линий. Сделайте чертежи. Для первой и третьей линии найдите уравнения касательных, параллельных прямой 2х + 3у = 6.

58. В ПДСК составьте каноническое уравнение гиперболы, если

а) уравнения её асимптот у = ± 3х, а уравнения директрис х = ± 4;

б) угол между асимптотами, содержащий ось (ОХ) равен 60⁰, а эксцентриситет равен 3/2.

59. В ПДСК составьте каноническое уравнение эллипса, если а) уравнения его директрис х = ± 4 и малая полуось равна 1,5;

б) он имеет общие фокусы с гиперболой 4х² - 9у² - 36 = 0 и его большая полуось равна 6.

60. В ПДСК заданы линии а) 4х² - 9у² - 36 = 0, б) 4х² - 9у² - 36 = 0, в) у² = 9х. Составьте уравнения этих линий в «стандартной» системе полярных координат и в той системе полярных координат, полярная ось которой совпадает с осью (ОХ).

61. Какие линии задают в полярной системе координат уравнения

а) , б), в)?

Запишите канонические уравнения этих линий.

62. Запишите уравнения цилиндрических поверхностей, каждая из которых задана уравнениями направляющей и координатами вектора, параллельного образующим. Сделайте чертёж. Система координат – прямоугольная.

а) ; б); в).

63. Запишите уравнения конических поверхностей, каждая из которых задана уравнениями направляющей и координатами вершины. Сделайте чертёж. Система координат – прямоугольная.

а) С (-5, 1, 2); б) С (0, 0, 0);

в) С (1, -2, 3).

64. Какие поверхности задают в ПДСК следующие уравнения? Сделайте чертёж. Если поверхность имеет прямолинейные образующие, то найдите их уравнения. Задайте некоторую точку на поверхности и найдите уравнения проходящих через неё прямолинейных образующих.

а) , б), в),

г) , д), е),

ж) , з).

ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНУ ПО КУРСУ «АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ»

12. Элементы векторной алгебры

1. Определение вектора, характеристики вектора.

2. Сложение векторов: определение, свойства.

3. Умножение вектора на действительное число: определение, свойства.

4. Коллинеарные векторы: определение, свойства, необходимые и достаточные условия коллинеарности двух векторов (три условия). Базис в пространстве коллинеарных векторов.

5. Компланарные векторы: определение, свойства, необходимые и достаточные условия компланарности трёх векторов (четыре условия). Базис в пространстве компланарных векторов.

6. Теорема о разложении вектора по трём некомпланарным векторам. Базис во множестве всех геометрических векторов.

7. Координаты вектора в данном базисе: определение, примеры, свойства. Действия с векторами в координатах. Преобразование координат.

8. Проекция на прямую параллельно данной плоскости: определение, свойства. Векторная проекция вектора, её свойства.

9. Числовая проекция вектора на ось, её свойства.

10. Ортогональная проекция вектора на ось, её свойства.

11. Скалярное произведение упорядоченной пары векторов: определение, свойства, формулы для вычисления. Применение скалярного произведения векторов к решению задач.

12. Векторное произведение упорядоченной пары векторов: определение, свойства, формула для вычисления, геометрический смысл. Применение векторного произведения к решению задач.

13. Двойное векторное произведение векторов.

14. Смешанное произведение упорядоченной тройки векторов: определение, свойства, формулы для вычисления, геометрический смысл. Применение смешанного произведения к решению задач.