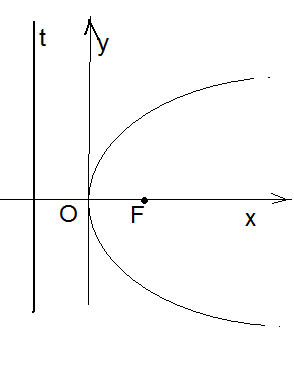- •Аналитическая геометрия
- •I. Элементы векторной алгебры
- •1.1. Геометрические векторы
- •1.2. Сложение векторов
- •1.3. Умножение вектора на действительное число
- •1.4. Коллинеарные векторы
- •1.5. Компланарные векторы
- •1.6. Проекция на прямую параллельно данной плоскости
- •1.7. Проекция вектора на ось
- •1.8. Ортогональная проекция вектора на ось
- •1.9. Скалярное произведение векторов
- •1.10. Векторное произведение векторов
- •1.15. Смешанное произведение векторов
- •II. Метод координат на плоскости и в пространстве
- •2.1 Введение системы аффинных и прямоугольных координат на плоскости и в пространстве
- •2.2. Аффинные задачи на плоскости и в пространстве
- •2.2.1. Координаты вектора, заданного координатами его концов.
- •2.3. Метрические задачи на плоскости и в пространстве .
- •2.3.1. Расстояние между точками.
- •2.3.2. Угол, заданный тремя точками.
- •2.4. Преобразование аффинных координат на плоскости и в пространстве
- •2.5. Преобразование прямоугольных координат на плоскости
- •2.6. Полярные координаты на плоскости
- •2.7. Цилиндрические и сферические координаты в пространстве
- •III. Образы первой ступени
- •3.1. Условия, определяющие фигуру в системе координат
- •3.2. Прямая в аффинной системе координат на плоскости и в пространстве
- •3.2.1. Уравнения прямой, проходящей через данную точку параллельно данному вектору
- •3.2.2. Уравнения прямой, проходящей через две точки
- •3.2.3. Общие уравнения прямой
- •I.Общее уравнение прямой на плоскости
- •2. Общие уравнения прямой в пространстве
- •3.2.4. Исследование взаимного расположения прямых
- •3.3. Прямая в прямоугольной системе координат на плоскости
- •3.3.1. Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору
- •3.3.2. Уравнение прямой, проходящей через данную точку под данным углом к оси (Ох)
- •3.3.3. Нормальное уравнение прямой
- •3.3.4. Угол между двумя прямыми, заданными общими уравнениями
- •3.3.5. Угол между наклонными прямыми, заданными уравнениями с угловыми коэффициентами
- •3.3.6. Расстояние от точки до прямой
- •3.4. Пучок прямых на плоскости
- •3.6. Прямая и плоскость в пространстве
- •3.6.1. Плоскость в аффинной системе координат
- •3.6.1.1. Уравнения плоскости, проходящей через данную точку параллельно двум данным векторам
- •3.6.1.2.. Уравнения плоскости, проходящей через три данные неколлинеарные точки
- •3.6.1.3. Общее уравнение плоскости
- •3.6.1.4. Исследование взаимного расположения двух плоскостей
- •3.6.2. Плоскость и прямая в прямоугольной системе координат
- •3.6.2.1. Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору
- •3.6.2.2. Угол между двумя плоскостями
- •3.6.2.3. Угол между прямой и плоскостью
- •3.6.2.4. Расстояние от точки до плоскости
- •3.6.2.5. Расстояние от точки до прямой
- •3.6.2.6. Расстояние между скрещивающимися прямыми
- •IV. Образы второго порядка
- •4.1. Элементарная теория линий второго порядка
- •4.1.1. Окружность
- •4.1.2. Эллипс
- •4.1.3. Гипербола
- •4.1.4. Парабола
- •4.1.5. Эллипс, гипербола и парабола в полярных координатах
- •4.2. Упрощение уравнения линии второго порядка
- •4.2.1. Преобразование уравнения линии второго порядка при повороте прямоугольной системы координат
- •4.2.2. Упрощение уравнения линии второго порядка. Метрическая классификация линий второго порядка
- •4.3. Поверхности
- •4.3.1. Цилиндрические поверхности
- •4.3.2. Конические поверхности
- •4.3.3. Поверхности вращения
- •4.3.4. Эллипсоид
- •4.3.5. Однополостный гиперболоид
- •4.3.6. Двуполостный гиперболоид
- •4.3.7. Эллиптический параболоид
- •4.3.8. Гиперболический параболоид
- •4.3.9. Прямолинейные образующие поверхности
- •V. Расширенные евклидовы плоскость и пространство
- •5.1. Определение расширенных евклидовых плоскости и пространства
- •5.2. Однородные координаты на расширенной евклидовой плоскости
- •5.3. Уравнения прямой, точки и линий второго порядка в однородных координатах на расширенной евклидовой плоскости
- •5.4. Однородные координаты в расширенном евклидовом пространстве
- •5.5. Уравнения плоскости и прямой в однородных координатах
- •Задачи по аналитической геометрии для домашних заданий
- •Метод координат на плоскости и в пространстве
- •Lll. Прямая линия на плоскости
- •LV. Плоскость и прямая в пространстве
- •V. Элементарная теория кривых второго порядка
- •Vl. Элементарная теория поверхностей
- •Vll. Другие системы координат на плоскости и в пространстве
- •Основная литература
4.1.4. Парабола
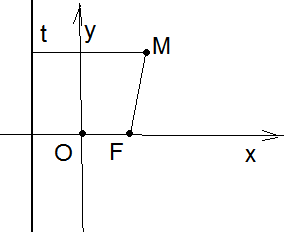
Определение 34. Параболой называется множество всех точек плоскости, каждая из которых равноудалёна от данной точки и от данной прямой (данная точка не лежит на данной прямой).
Данная точка F называется фокусом параболы, а данная прямая t – её директрисой.
|
Выберем прямоугольную систему координат так, чтобы ось (ОХ) проходила через фокус перпендикулярно директрисе в сторону от директрисы к фокусу. За начало координат возьмём середину отрезка между директрисой и фокусом (рис. 71). М параболе FМ = d(М, t) ().
Обозначим d(F,
t) = р.
Тогда F( |
Рис. 71 |
будет иметь
уравнение
х =
![]() .
Равенство ()
перепишется
.
Равенство ()
перепишется
![]() .
Получили уравнение параболы. Так как
обе части равенства неотрицательны, то
возведение в квадрат даст эквивалентное
уравнение
.
Получили уравнение параболы. Так как
обе части равенства неотрицательны, то
возведение в квадрат даст эквивалентное
уравнение
у2 = 2рх (61).
Полученное уравнение называется каноническим уравнением параболы. В этом уравнении р 0. Из уравнения (61) следуют свойства:
|
парабола лежит в той полуплоскости с границей (ОУ), в сторону которой направлена ось (ОХ); парабола симметрична относительно оси (ОХ); при х у ; парабола проходит через начало координат и не имеет других точек пересечения с осями координат. Начало координат называется вершиной параболы. |
Рис. 72 |
Если М0(х0, у0) параболе, то уравнение касательной к параболе в этой точке имеет вид уу0 = р(х + х0).
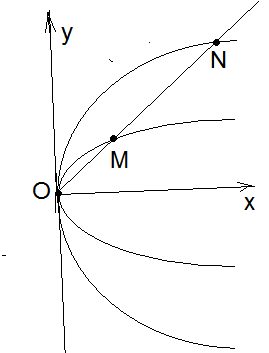
Теорема 7. Любые две параболы подобны.
|
Доказательство.
Пусть у2
= 2рх
и у2
= 2р1х
две параболы. Пусть у
= кх
– любая прямая, проходящая через
начало координат. Пусть эта прямая
пересекает параболы в точках М
и .
Тогда, если прямая проходит в первом
координатном углу, то М(х1, |
Рис. 73 |
![]() .
Отсюда
.
Отсюда
![]() ,
т.е. параболы подобны с коэффициентом
подобия
,
т.е. параболы подобны с коэффициентом
подобия![]() .
.
Замечание 1. Если вершиной параболы является точка С(х0, у0) и ось параболы параллельна оси (ОХ), то парабола имеет уравнение
(у – у0)2 = 2р(х – х0).
Замечание 2. Если в уравнении (7) р 0, то парабола располагается в той полуплоскости с границей (ОУ), в которой лежит отрицательная полуось (ОХ). Уравнение х2 = 2ру при любом р задаёт параболу, симметричную относительно оси (ОУ).
Общие свойства эллипса, гиперболы и параболы описывает следующая
Теорема 8. Для любых данных прямой t и точки F (F t) множество точек, отношение расстояний от каждой из которых до данной точки и до данной прямой есть постоянная величина , есть либо эллипс, либо гипербола, либо парабола.
4.1.5. Эллипс, гипербола и парабола в полярных координатах
Если в каноническом
уравнении эллипса, гиперболы или параболы
заменить
![]() то получим уравнение соответствующей
линии в той системе полярных координат,
полюс которой совпадает с началом ПДСК,
а полярная ось совпадает с осью (ОЗ).
Уравнения, очевидно, будут различными.
Но существует такая система полярных
координат, в которой уравнения всех
трёх линии имеют одинаковый вид.
то получим уравнение соответствующей
линии в той системе полярных координат,
полюс которой совпадает с началом ПДСК,
а полярная ось совпадает с осью (ОЗ).
Уравнения, очевидно, будут различными.
Но существует такая система полярных
координат, в которой уравнения всех
трёх линии имеют одинаковый вид.
Зададим систему
полярных координат так, что а) в случае
эллипса полюс совпадает с фокусом F1,
а полярная ось имеет направление
![]() ;
б) в случае гиперболы полюс совпадает
с фокусомF2,
а полярная ось имеет направление
;
б) в случае гиперболы полюс совпадает
с фокусомF2,
а полярная ось имеет направление
![]() ;
в) в случае параболы полюс совпадает
с её единственным фокусом, а полярная
ось направлена по оси параболы в сторону
от её вершины (рис. 74).
;
в) в случае параболы полюс совпадает
с её единственным фокусом, а полярная
ось направлена по оси параболы в сторону
от её вершины (рис. 74).
|
|
Рис. 74 |
|
|
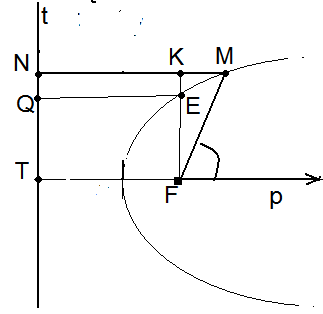
Пусть для
эллипса, параболы или «правой» ветви
гиперболы (обозначим их )
зафиксирована указанная система
полярных координат, пусть М(,
)
и пусть t
– директриса,
соответствующая выбранному фокусу.
Тогда М
|
Рис. 75 | |
т.к. точка Е
лежит на .
Если обозначить EF=
h,
то QЕ=
![]() .
Следовательно,М=
соs
+
.
Следовательно,М=
соs
+
![]() .
Итак,М
.
Итак,М
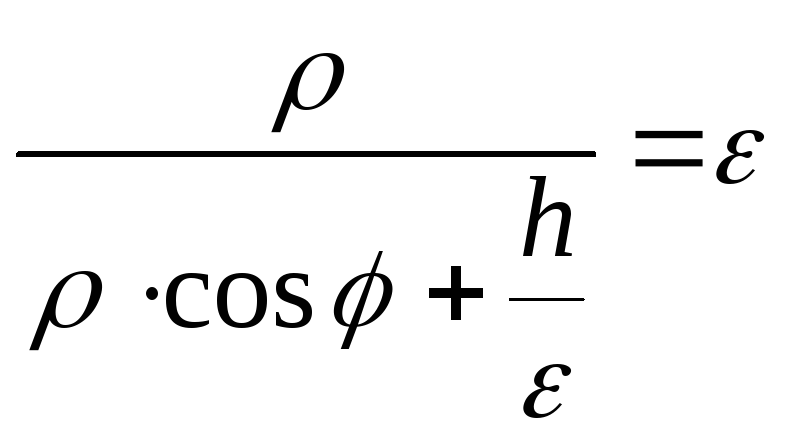 .
Преобразуя это уравнение, получим
.
Преобразуя это уравнение, получим![]() (62)
(62)
При 1 уравнение (62) задаёт эллипс, при 1 оно задаёт «правую» ветвь гиперболы, при = 1 – параболу.
Для эллипса и
гиперболы Е(
с,
![]() ). Следовательно,h
=
). Следовательно,h
=
![]() .
Для параболы (если её уравнениеу2
= 2рх) h
= р.
.
Для параболы (если её уравнениеу2
= 2рх) h
= р.