1.6. Проекция на прямую параллельно данной плоскости

Пусть l – прямая, П – плоскость и l П. Пусть М – произвольная

точка. Через точку М проведём плоскость П1, параллельную П. Пусть М1 = l  П1. Точка М1 называется проекцией точки М на прямую l параллельно плоскости П. Свойства проекций. 10. Каждая точка имеет проекцию и только одну. 20. Точка совпадает со своей проекцией

Рис. 12

тогда и только тогда, когда она лежит на прямой l.

3⁰. Точки имеют одну и ту же проекцию тогда и только тогда, когда они лежат в одной плоскости, параллельной П.

4⁰. Если отрезок параллелен плоскости П, то он проектируется в точку. Если отрезок не параллелен плоскости П, то его проекция – отрезок.

5⁰. Проекция ориентированного отрезка есть ориентированный отрезок. Следовательно, проекцией вектора будет вектор. Он называется векторной проекцией данного вектора и обозначается (параллельноП). Если проектирование идёт параллельно только одной плоскости, то слова в скобках можно опускать.

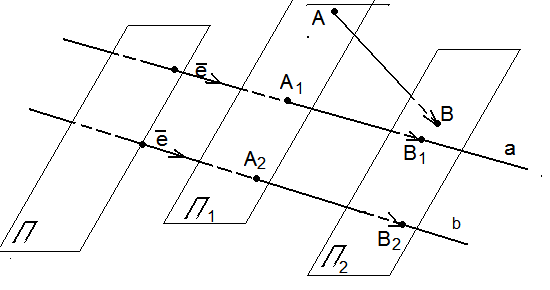
6⁰. Равные и параллельные отрезки имеют равные проекции.

Доказательство. Пусть отрезки АВ и СD равны и параллельны. Если АВ параллелен плоскости П, то СD тоже параллелен плоскости П. В этом случае оба отрезка проектируются в точку. Следовательно, их проекции равны.

Рис. 13

Пусть АВ, а поэтому и СD, не параллельны плоскости П. Пусть АВ проектируется в А₁В₁, а СD  в С₁D₁. При параллельном переносе на вектор ПлоскостьП₁ перейдёт в П₃, П₂  в П₄, прямая l  сама в себя. Следовательно, все отрезки с концами в плоскостях П₁ и П₂ перейдут в некоторые отрезки с концами в плоскостях П₃ и П₄. Отсюда и следует, что А₁В₁ равен и параллелен С₁D₁.

7⁰. Если , то=.

Доказательство. Так как равные векторы имеют равные векторные проекции, то при сложении первый вектор можно отложить от любой точки. Пусть О  l, . ЕслиА  А1, В  В1, то =,=,. Так как, то+.

Рис. 14

8⁰. =. (Докажите самостоятельно)

1.7. Проекция вектора на ось

Определение 9. Осью называется прямая с фиксированным на ней единичным вектором. Этот вектор называется ортом оси.

Пусть  орт оси,  произвольный вектор, =. Так как векторыиколлинеарны и, то=. Число называется

числовой проекцией вектора на данную ось и обозначается прl. Из 70 и 80 свойств векторных и числовых проекций следует и. 90. Векторные и числовые проекции вектора на сонаправленные оси параллельно одной и той же плоскости равны.

Рис. 15

Доказательство. Сонаправленные оси имеют один и тот же орт. Если и, то(по свойству отрезков параллельных прямых, заключённых между параллельными плоскостями). Итак,

Рис. 16

векторные проекции вектора на сонаправленные оси равны. Так как у этих осей один и тот же орт, то числовые проекции тоже равны.

10⁰. Так как направление оси можно задавать любым ненулевым вектором, сонаправленным с ортом оси, то можно говорить о проекции одного вектора на направление другого и обозначать ( проекция векторана направление векторапараллельно плоскостиП).