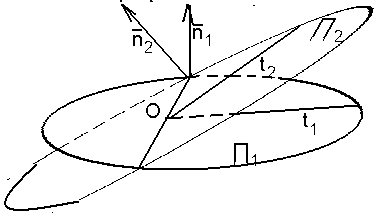
3.6.2.2. Угол между двумя плоскостями

Дано: ,П1 : А1х + В1у + С1z + D1 = 0, П2 : А2х + В2у + С2z + D2 = 0. Найти один из углов между П1 и П2 . Решение. Из уравнений П1 и П2 следует, что иперпендикулярны плоскостямП1 и П2 соответственно. Если О – точка на линии пересечения П1 и П2, t1 и t2 лежат в плоскостях П1 и П2, проходят через

Рис. 49

точку О и перпендикулярны линии пересечения этих плоскостей (рис. 49), то = (П₁,П₂). Но по свойству углов со взаимно перпендикулярными сторонами либо равен углу, либо дополняет его до 180⁰. И в том, и в другом случае равен одному из углов междуП₁ и П₂ . Следовательно,

Cos((П₁,П₂) = (49)

Из формулы (49) следует, что П₁  П₂  = 0.

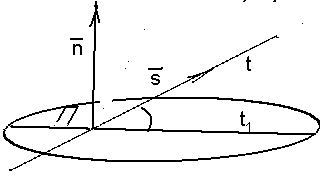
3.6.2.3. Угол между прямой и плоскостью

Дано: ,П : Ах + Ву + Сz + D = 0, t : . Найти один из углов между П и t. Решение. Угол между прямой и плоскостью – это угол между прямой и её ортогональной проекцией на плоскость (рис. 35). Из уравнений

Рис. 50

прямой и плоскости вектор перпендикулярен плоскостиП, а вектор параллелен прямой t. Следовательно,

).

Отсюда следует, что

sin(П, = (50)

Из свойств векторов иследует:

П  t  ;П  t  (51)

3.6.2.4. Расстояние от точки до плоскости

Дано: ,П : Ах + Ву + Сz + D = 0, М(х0, у0, z0). Найти расстояние d(M0, П) от точки М0 до плоскости П. Из уравнения плоскости П следует, что вектор перпендикулярен плоскостиП. Опустим из точки М0 перпендикуляр NM0 на плоскость П (рис. 51). Пусть N(x1, y1, z1). Тогда Ax1 + By1 + Cz1 + D = 0 (). Искомое расстояние d(M0, П) = ()

Рис. 51

Вектор коллинеарен с вектором. Так как, то(). Отсюда и из равенства () следует, что d(M₀, П) = =(). Итак, задача свелась к нахождению . Умножим скалярно на обе части равенства (), получим . Перейдя к координатам и учитывая, что система координат прямоугольная, получим

A(x₀  x₁) + B(y₀  y₁) + C(z₀  z₁) = (A² + B² + C²).

Так как A² + B² + C²  0, то . Из равенства () следует, что =D. Итак, . Подставив в (), получим

d(M₀, П) = (52)

Задача 18. Дано: ,П : 12х + 3у  4z  35 = 0.

Найдите уравнения плоскостей, параллельных П и отстоящих от неё на расстоянии 5.

Решение. Обозначим искомые плоскости П₁ и П₂ . Тогда М  (П₁  П₂)  d(M, П) = 5. Используя формулу (52), получим М  (П₁  П₂)  . После упрощения получим. Раскрывая модуль, получим уравнения двух плоскостей:

П₁ : 12х + 3у  4z  80 = 0 и П₂ : 12х + 3у  4z + 10 = 0.

3.6.2.5. Расстояние от точки до прямой

Дано: ,l : , М1(x1, y1, z1). Найти расстояние d (M1, l). Из уравнений прямой l следует, что точка M0 (x0, y0, z0 ) лежит на прямой l и вектор параллелен этой прямой. Искомое расстояние равно высоте параллелограмма,

Рис. 52

построенного на векторах икак на сторонах (рис. 52).

Следовательно,

.

Переписав это равенство в координатах, получим

(53)