1.8. Ортогональная проекция вектора на ось

Определение 10. Проектирование называется ортогональным, Если плоскость П ортогональна оси.

При ортогональном проектировании достаточно из данной точки опустить на ось перпендикуляр.

Теорема 7. Числовая ортогональная проекция вектора на ось равна произведению длины этого вектора на косинус его угла с осью.

Доказательство. Пусть l – ось,  её орт,  произвольный вектор. Если , топр_l = 0, поэтому можно считать, что утверждение теоремы верно. Пусть и = (l).

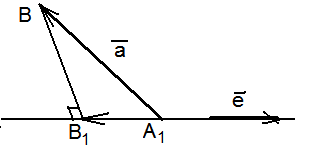
Возможны следующие случаи. 1)  = 0. В этом случае (рис. 17а) ипр=.

Рис. 17 а)

Рис. 17 б)

2) 0    90⁰. В этом случае (рис. 17б) ,пр.

Рис. 17 в)

Рис. 17 г)

Рис. 17 д)

3)  = 90⁰ (рис. 17в). В этом случае пр= 0 и, следовательно, пр= .

4) 90⁰    180⁰ (рис. 17г). В этом случае ,пр.

5)  = 180⁰ (рис. 17д). В этом случае пр=.

Итак, во всех случаях пр.

1.9. Скалярное произведение векторов

В разделе «Линейные пространства» в линейных пространствах над полем действительных чисел вводилась ещё одна операция: скалярное произведение векторов, с помощью которой линейное пространство превращалось в евклидово пространство. Если в данном линейном пространстве по разному вводить скалярное произведение, то получатся различные евклидовы пространства. В векторном пространстве геометрических векторов существует «стандартное» (исторически сложившееся благодаря потребностям физики) определение скалярного произведения векторов.

Определение 11. Скалярным произведением упорядоченной пары ненулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними. Если хотя бы один из перемножаемых векторов нулевой, то скалярное произведение считается равным нулю.

Обозначение: (), или. Из определения

= (1)

Свойства скалярного произведения.

1⁰. Скалярное произведение любой упорядоченной пары векторов определено и однозначно.

2⁰. =для любых векторови(коммутативный закон).

Доказательство. Если =или=, то= 0 и= 0, т.е. равенство верно.

Пусть  и . Тогда==.

3⁰. Если  и , то=пр. Если  , а=, то тоже=пр.Следовательно, при  имеет место формула= пр(2)

4⁰. = 0 либо =, либо=, либо .

5⁰. (+)=, для любых векторов,и.

Доказательство. Если вектор , то доказываемое равенство имеет вид 0 = 0 + 0, т.е. оно верно. Пусть. Тогда (по формуле 2)

(+)==.

6⁰. для любых векторов,и любого действительного числа.

Доказательство. Если либо  = 0, либо хотя бы один из векторов ,нулевой, то равенство очевидно. Пусть  0 и векторы ,нулевые. Тогда

.

Произведение называется скалярным квадратом вектораи обозначается

= .

7⁰. =для любого вектора. Отсюда следует

. (3)

Из формулы (7) следует, что  0 для любого вектора и= 0 .

Теорема 8. Множество всех геометрических векторов, любое множество всех компланарных векторов и любое множество всех коллинеарных векторов являются евклидовыми пространствами.

Доказательство следует из свойств 1⁰, 2⁰, 4⁰, 7⁰.

8⁰. Если  , то. (4)

Формула (4) следует из (2).

9⁰. Если  и , то

. (5)

Замечание. Формулы 4⁰, 7⁰ – 10⁰ определяют применение скалярного произведения для решения задач.

10⁰. (Скалярное произведение в координатах)

Пусть В =  базис, ,. Тогда

)=. (6)

Если базис В = ортонормированный, то

= . (7)

Из формулы (3) получаем, что в ортонормированном базисе

. (8)

Замечание. Формулы (6), (7) и (8) выведены в векторном пространстве всех геометрических векторов. Во множестве компланарных векторов, в базисе В = получим, а в ортонормированном базисе=и. Во множестве коллинеарных векторов, в базисеВ = получим=. Если= 1, то=и.

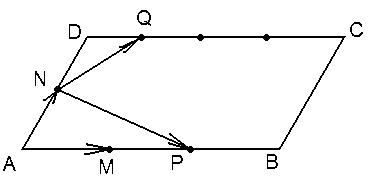
Задача 7. В параллелограмме АВСD угол DАВ = 60⁰, ,,

, AB = 6, AD = 4. Найдите QNP (рис. 18). Решение. Решим задачу векторным методом. Для этого выберем базис , где(),. УголQNP равен углу между векторами и. Используя формулу (5), получим Cos(QNP) = . Найдём эти

Рис. 18

векторы: ,. Поэтому. Так как= 2² = 4, = 2² = 4, (= 22Cos60⁰ = 2, то =. Аналогично,,. Следовательно,

Cos(QNP) = .

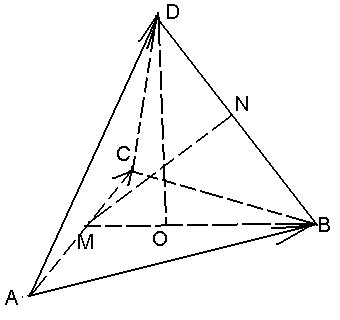
Задача 8. Докажите, что в правильном тетраэдре а) противоположные рёбра взаимно перпендикулярны, б) отрезок, соединяющий середины противоположных рёбер, перпендикулярен к ним и найдите длину этого отрезка, если длина ребра равна а.

Решение. Решим задачу векторным методом. В качестве базиса выберем векторы ,,. Так как тетраэдр правильный, то достаточно рассмотреть одну пару противоположных рёбер и один из отрезков, соединяющих середины противоположных рёбер. Покажем, что,и. Для этого достаточно найти скалярные произведения,и. Выражая

Рис. 19

векторы через базис, получим ,,

. Следовательно,===ааCos60⁰  ааCos60⁰ = 0, т.е. .

= Отсюда. Аналогично доказывается, что.

По формуле (8) получаем, что

.