- •Аналитическая геометрия
- •I. Элементы векторной алгебры
- •1.1. Геометрические векторы
- •1.2. Сложение векторов
- •1.3. Умножение вектора на действительное число
- •1.4. Коллинеарные векторы
- •1.5. Компланарные векторы
- •1.6. Проекция на прямую параллельно данной плоскости
- •1.7. Проекция вектора на ось
- •1.8. Ортогональная проекция вектора на ось
- •1.9. Скалярное произведение векторов
- •1.10. Векторное произведение векторов
- •1.15. Смешанное произведение векторов
- •II. Метод координат на плоскости и в пространстве
- •2.1 Введение системы аффинных и прямоугольных координат на плоскости и в пространстве
- •2.2. Аффинные задачи на плоскости и в пространстве
- •2.2.1. Координаты вектора, заданного координатами его концов.
- •2.3. Метрические задачи на плоскости и в пространстве .
- •2.3.1. Расстояние между точками.
- •2.3.2. Угол, заданный тремя точками.
- •2.4. Преобразование аффинных координат на плоскости и в пространстве
- •2.5. Преобразование прямоугольных координат на плоскости
- •2.6. Полярные координаты на плоскости
- •2.7. Цилиндрические и сферические координаты в пространстве
- •III. Образы первой ступени
- •3.1. Условия, определяющие фигуру в системе координат
- •3.2. Прямая в аффинной системе координат на плоскости и в пространстве
- •3.2.1. Уравнения прямой, проходящей через данную точку параллельно данному вектору
- •3.2.2. Уравнения прямой, проходящей через две точки
- •3.2.3. Общие уравнения прямой
- •I.Общее уравнение прямой на плоскости
- •2. Общие уравнения прямой в пространстве
- •3.2.4. Исследование взаимного расположения прямых
- •3.3. Прямая в прямоугольной системе координат на плоскости
- •3.3.1. Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору
- •3.3.2. Уравнение прямой, проходящей через данную точку под данным углом к оси (Ох)
- •3.3.3. Нормальное уравнение прямой
- •3.3.4. Угол между двумя прямыми, заданными общими уравнениями
- •3.3.5. Угол между наклонными прямыми, заданными уравнениями с угловыми коэффициентами
- •3.3.6. Расстояние от точки до прямой
- •3.4. Пучок прямых на плоскости
- •3.6. Прямая и плоскость в пространстве
- •3.6.1. Плоскость в аффинной системе координат
- •3.6.1.1. Уравнения плоскости, проходящей через данную точку параллельно двум данным векторам
- •3.6.1.2.. Уравнения плоскости, проходящей через три данные неколлинеарные точки
- •3.6.1.3. Общее уравнение плоскости
- •3.6.1.4. Исследование взаимного расположения двух плоскостей
- •3.6.2. Плоскость и прямая в прямоугольной системе координат
- •3.6.2.1. Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору
- •3.6.2.2. Угол между двумя плоскостями
- •3.6.2.3. Угол между прямой и плоскостью
- •3.6.2.4. Расстояние от точки до плоскости
- •3.6.2.5. Расстояние от точки до прямой
- •3.6.2.6. Расстояние между скрещивающимися прямыми
- •IV. Образы второго порядка
- •4.1. Элементарная теория линий второго порядка
- •4.1.1. Окружность
- •4.1.2. Эллипс
- •4.1.3. Гипербола
- •4.1.4. Парабола
- •4.1.5. Эллипс, гипербола и парабола в полярных координатах
- •4.2. Упрощение уравнения линии второго порядка
- •4.2.1. Преобразование уравнения линии второго порядка при повороте прямоугольной системы координат
- •4.2.2. Упрощение уравнения линии второго порядка. Метрическая классификация линий второго порядка
- •4.3. Поверхности
- •4.3.1. Цилиндрические поверхности
- •4.3.2. Конические поверхности
- •4.3.3. Поверхности вращения
- •4.3.4. Эллипсоид
- •4.3.5. Однополостный гиперболоид
- •4.3.6. Двуполостный гиперболоид
- •4.3.7. Эллиптический параболоид
- •4.3.8. Гиперболический параболоид
- •4.3.9. Прямолинейные образующие поверхности
- •V. Расширенные евклидовы плоскость и пространство
- •5.1. Определение расширенных евклидовых плоскости и пространства
- •5.2. Однородные координаты на расширенной евклидовой плоскости
- •5.3. Уравнения прямой, точки и линий второго порядка в однородных координатах на расширенной евклидовой плоскости
- •5.4. Однородные координаты в расширенном евклидовом пространстве
- •5.5. Уравнения плоскости и прямой в однородных координатах
- •Задачи по аналитической геометрии для домашних заданий
- •Метод координат на плоскости и в пространстве
- •Lll. Прямая линия на плоскости
- •LV. Плоскость и прямая в пространстве
- •V. Элементарная теория кривых второго порядка
- •Vl. Элементарная теория поверхностей
- •Vll. Другие системы координат на плоскости и в пространстве
- •Основная литература
1.15. Смешанное произведение векторов
Определение 14. Смешанным произведением упорядоченной тройки векторов называется результат векторного произведения первых двух векторов, умноженный скалярно на третий вектор.
Если дана
упорядоченная тройка векторов
![]() ,
,![]() и
и![]() ,
то смешанным произведением будет число,
равное
,
то смешанным произведением будет число,
равное![]() .
.
Свойства смешанного произведения векторов.
10. Смешанное произведение любой упорядоченной тройки векторов определено и однозначно.
20.
Очевидно, смешанное произведение
обладает всеми свойствами, общими для
векторного и скалярного произведений.
Так, например,
![]() ,
,
![]() )
)![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
30. Смешанное произведение трёх векторов равно нулю тогда и только тогда, когда данные векторы компланарны.
Доказательство.
![]() = 0
= 0
![]() =
=![]() ,
или
,
или![]() ,
или
,
или![]() .
.
Но
![]() =
=![]()
![]() и
и![]() коллинеарны;
коллинеарны;![]()
![]() параллелен плоскости векторов
параллелен плоскости векторов![]() и
и![]() .
.
Следовательно,
![]() = 0
= 0
![]() ,
,![]() и
и![]() компланарны.
компланарны.
40. (Смешанное произведение в координатах).
Доказательство.
Пусть В =
![]() ортонормированный
базис,
ортонормированный
базис,
![]() ,
,![]() ,
,![]() .
Так как
.
Так как![]() =
=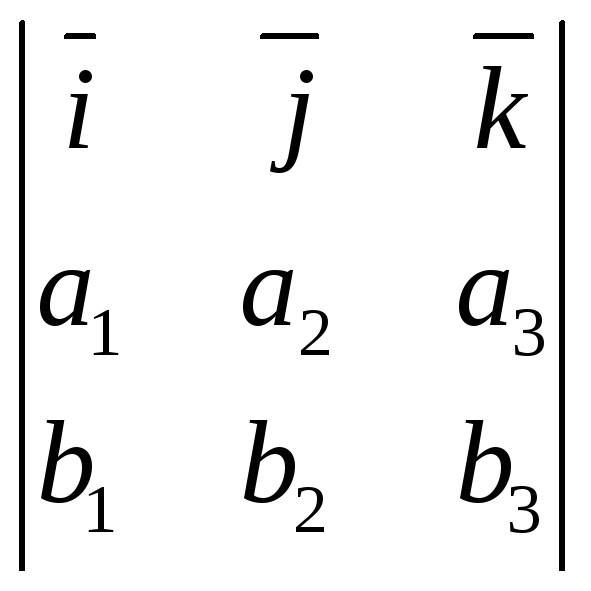 =
=![]() .
Так как базис ортонормированный, то по
формуле (7) получим
.
Так как базис ортонормированный, то по
формуле (7) получим
![]() =
=
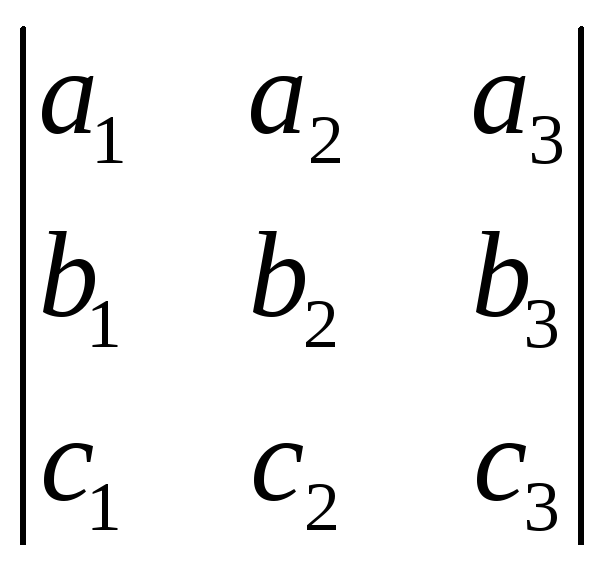 (11)
(11)
50. Если в смешанном произведении поменять местами два множителя, то оно сменит знак.
Доказательство. Зафиксируем ортонормированный базис. Тогда смешанное произведение можно найти по формуле (11). Если два множителя в смешанном произведении меняются местами, то в определителе формулы (11) меняются местами две строки. При этом определитель меняет знак на противоположный.
60. Если в смешанном произведении все множители поменять местами, то смешанное произведение не изменится. (Докажите)
70.
Смешанное произведение не изменится,
если в нём поменять местами знаки
векторного и скалярного умножения,
т.е.
![]() =
=![]()
Доказательство.
Зафиксируем
ортонормированный базис. Тогда
![]() =
=![]() =
=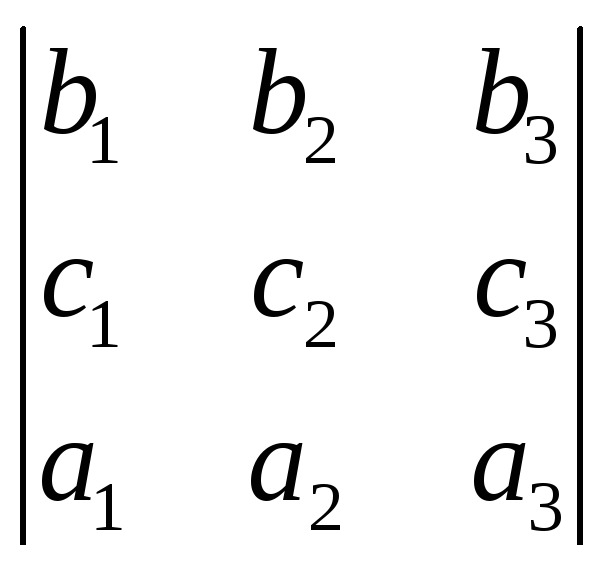 =
= =
=![]() .
.
Замечание.
Последнее свойство позволяет в обозначении
смешанного произведения не ставить
знаки векторного и скалярного произведений,
поэтому смешанное произведение можно
обозначать
![]() .
.
80. Геометрический смысл модуля и знака смешанного произведения.
Если векторы
компланарны, то смешанное произведение
их равно нулю (свойство 30),
поэтому рассмотрим упорядоченную
тройку
![]() ,
,![]() и
и![]() некомпланарных векторов. Отложим векторы
некомпланарных векторов. Отложим векторы![]() ,
,![]() и
и![]() от одной точки:
от одной точки:
|
|
Рис. 27 |
тройка
![]() ,
,![]() ,
,![]() левая, то вектор
левая, то вектор![]() противоположно направлен с вектором
противоположно направлен с вектором![]() ,
следовательно, числовая проекция
,
следовательно, числовая проекция![]()
0. Так как
0. Так как
![]() =
=![]() ,
то знак
,
то знак![]() совпадает со знаком
совпадает со знаком![]() .
Итак,
.
Итак,![]()
0
тройка векторов
0
тройка векторов
![]() ,
,![]() ,
,![]() правая и
правая и![]()
0
тройка векторов
0
тройка векторов
![]() ,
,![]() ,
,![]() левая.
левая.
Так как![]() =
=
![]() =
=![]() ,
где
,
где![]()
высота параллелепипеда, то
высота параллелепипеда, то ![]()
=
=
![]() ,
где
,
где![]()
объём параллелепипеда OADBCMNP.
объём параллелепипеда OADBCMNP.
90.
![]() (формула для нахождения высоты
параллелепипеда).
(формула для нахождения высоты
параллелепипеда).
100.
Если АВСD
тетраэдр, то
![]() ,
,![]() .
.
Задача 11.
АВСDA1B1C1D1
куб с единичным ребром,
![]() ,
,
|
Решение.
|
Рис. 28 |
Найдём координаты
векторов:
![]() ,
,![]() ,
,
![]() .
Следовательно,
.
Следовательно,
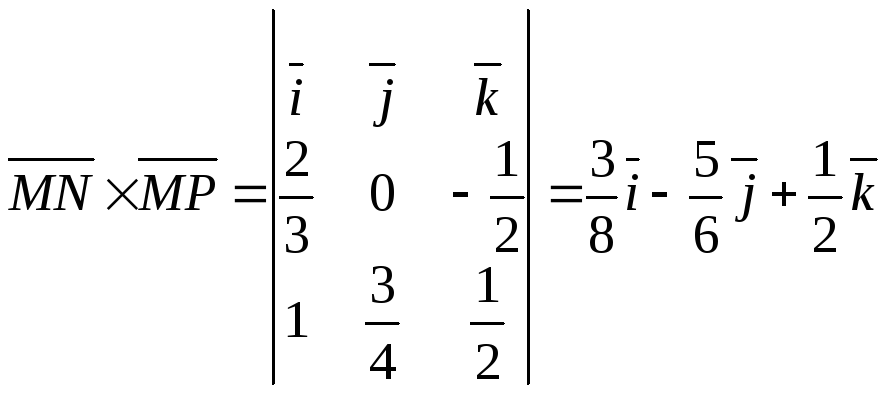 ,
,
![]() ,
,
![]() .
.
![]() =
=
![]() ,
,![]() .
Следовательно,
.
Следовательно,
![]() .
.