1.10. Векторное произведение векторов

Определение 12. Упорядоченная тройка некомпланарных векторов называетсяположительно ориентированной (правой), если при откладывании этих векторов от одной точки кратчайший поворот от вектора к векторус конца векторавиден против часовой стрелки. В противном случае данная тройка векторов называетсяотрицательно ориентированной (левой).

Определение 13. Векторным произведением упорядоченной пары неколлинеарных векторов иназывается вектор, удовлетворяющий условиям:

• 

• ,

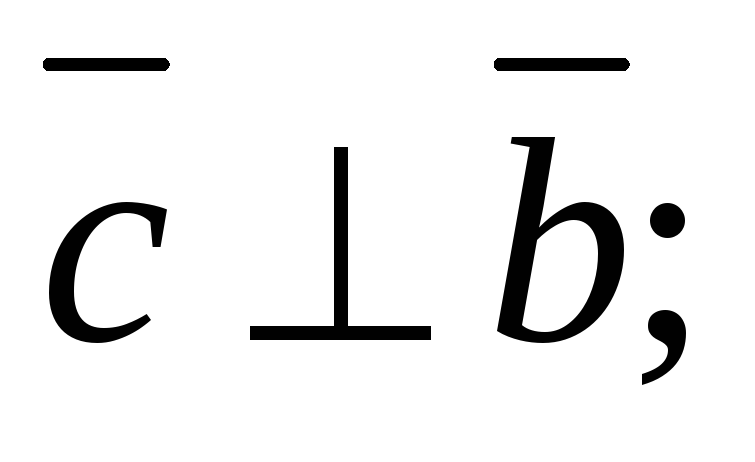
• упорядоченная тройка векторов 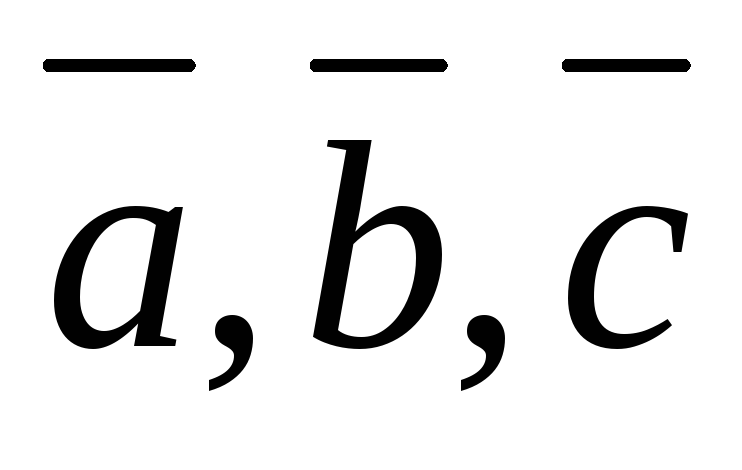положительно ориентирована.

Если векторы иколлинеарны, то их векторным произведением считается нулевой вектор.

Векторное произведение упорядоченной пары векторов иобозначаетсяили.

Примеры. 1. Пусть  положительно ориентированная тройка единичных взаимно перпендикулярных векторов (рис. 23). Найдём их попарные векторные произведения.

Пусть . Тогда. Кроме того,и тройка правая. Следовательно, , т.е.. Аналогично получим, что,,,,. 2. АВСD  правильный тетраэдр с ребром 1 (из точки D обход точек А, В, С виден по часовой стрелке), [DO]  его высота. Найдём .

Рис. 23

Решение. В правильном тетраэдре с ребром 1 длина высоты равна (т.е., гдеО – проекция точки D на плоскость (АВС)). Пусть . Тогда(рис. 24). Кроме того,

, , т.е.. Так как тройка векторовдолжна быть правой, а тройкалевая, то векторпротивонаправлен с вектором. Сравнивая длины векторови, получаем. Свойства векторного произведения векторов. 10. Векторное произведение любой

Рис. 24

упорядоченной пары векторов определено и однозначно.

2⁰. = для любых векторови.

3⁰. для любых векторовии любого действительного числа .

4⁰. для любых векторов,и.

5⁰. = иколлинеарны.

60. Если векторы ине коллинеарны, то длина вектора, равного их векторному произведению, численно равна площади параллелограмма, построенного на этих векторах как на сторонах. Доказательство. (рис. 25). 70. (Векторное произведение в координатах).

Рис. 25

Пусть В =  базис, ,. Тогда

= )=

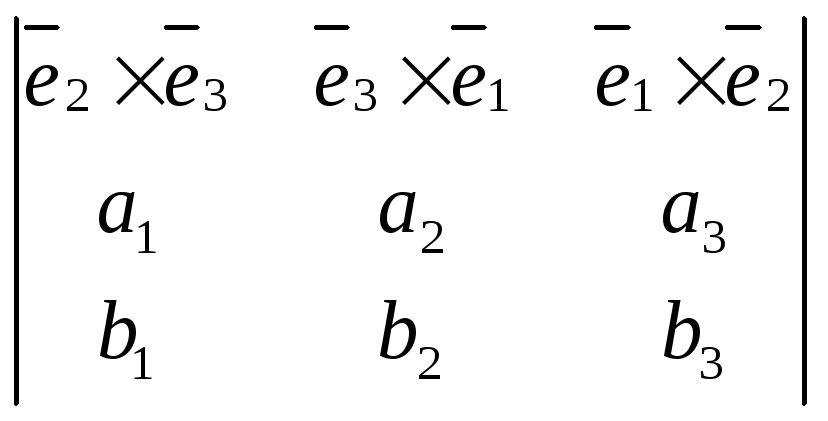= (9)

Если базис В = ортонормированный, то, используя пример 1, получим

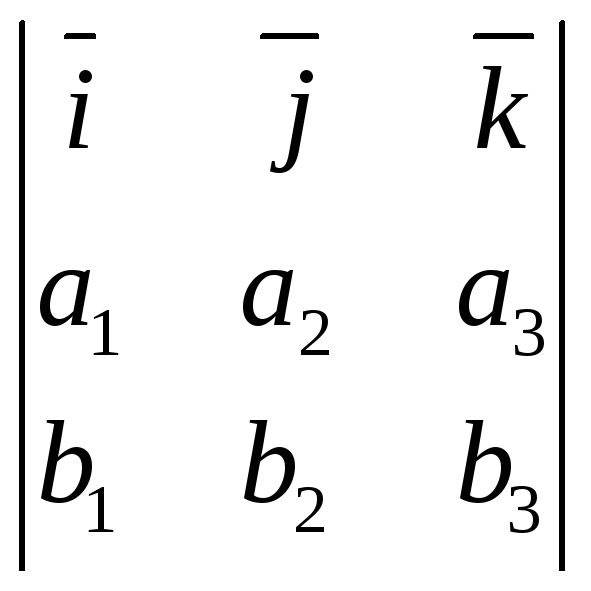= (10)

Задача 9. В ортонормированном базисе ,,. Найдите ()и.

Решение. Используем формулу (10). Получим

= ,

()=.

= ,

.

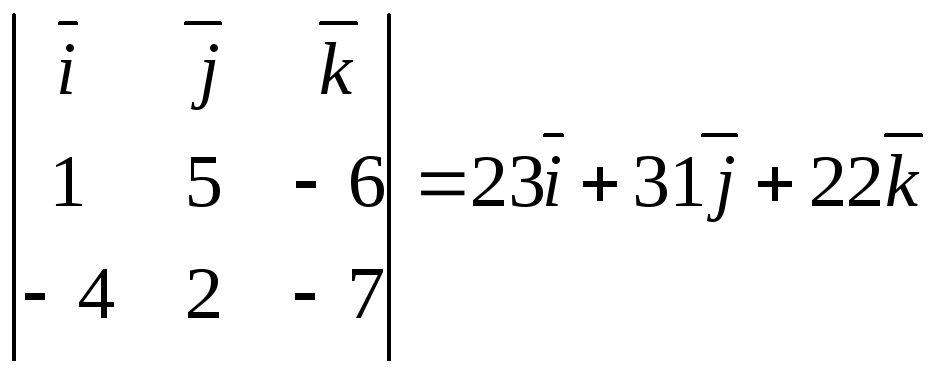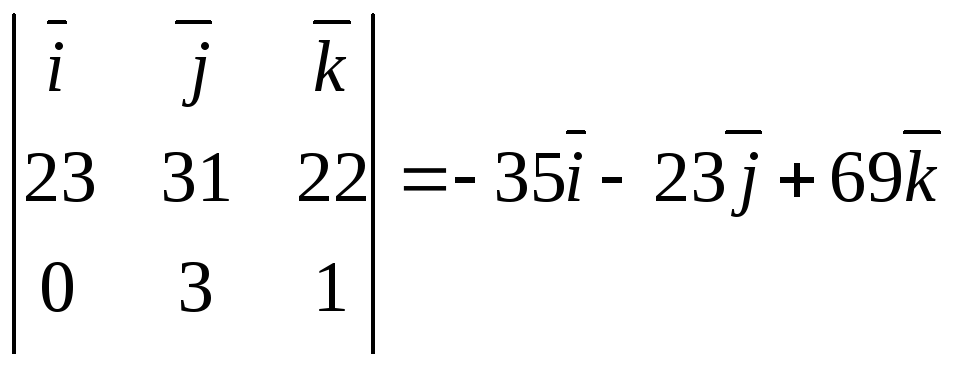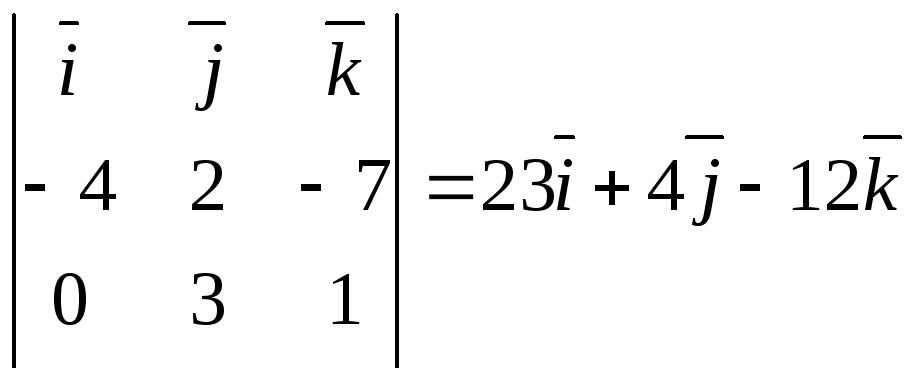Из результатов решения этой задачи видно, что ()не обязано быть равно, т.е. векторное умножение векторов не подчиняется ассоциативному закону.

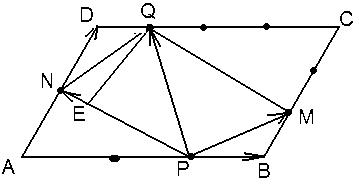
Задача 10. В параллелограмме АВСD угол DАВ = 60⁰, ,,,,AB = 6, AD = 4. Найдите площадь четырёхугольника MQNP и длину его высоты QE, опущенной из вершины Q.

Решение. Разобьём четырёхугольник MQNP на два треугольника, тогда . Так как длины векторов ии угол между ними известны, то выберем базис,. Тогда. Отсюда.

Рис. 26

. .

Найдём указанные выше векторные произведения.

Отсюда

.

Аналогично,

Отсюда .

Следовательно, .

Искомая высота является высотой в треугольнике QNP. Следовательно, . Находя длину вектора, получим

==. Следовательно, .