5.3. Уравнения прямой, точки и линий второго порядка в однородных координатах на расширенной евклидовой плоскости

Пусть система однородных координат задана с помощью базиса исоответствующий аффинный репер. Пустьl  произвольная собственная прямая на данной плоскости. Пусть на плоскости до расширения она имела уравнение Ах + Ву + С = 0. Используя формулы (*), получим, что однородные координаты всех собственных точек данной прямой будут удовлетворять уравнению , илиAX + BY + CZ = 0. Подставив в полученное уравнение координаты несобственной токи этой прямой, получим , т.е координаты несобственной точки тоже удовлетворяют полученному уравнению. Итак, еслиАх + Ву + С = 0 аффинное уравнение собственной прямой, то AX + BY + CZ = 0 её уравнение в однородных координатах. Обратно, всякое уравнение вида AX + BY + CZ = 0, где А и В не равны нулю одновременно, является уравнением прямой в однородных координатах. Так как несобственная прямая имеет уравнение Z = 0, то уравнения AX + BY + CZ = 0, где А, В и С не равны нулю одновременно, и только они являются уравнениями рямой в однородных координатах.

Так как уравнения AX + BY + CZ = 0 и AX + BY + CZ = 0 при любом   0 задают одну и ту же прямую, то между всеми прямыми расширенной евклидовой плоскости и всеми ненулевыми классами пропорциональных троек [А: В: С] устанавливается взаимнооднознаное соответствие. Следовательно, отношение [А: В: С] вполне определяет прямую на расширенной плоскости и называется её однородными координатами.

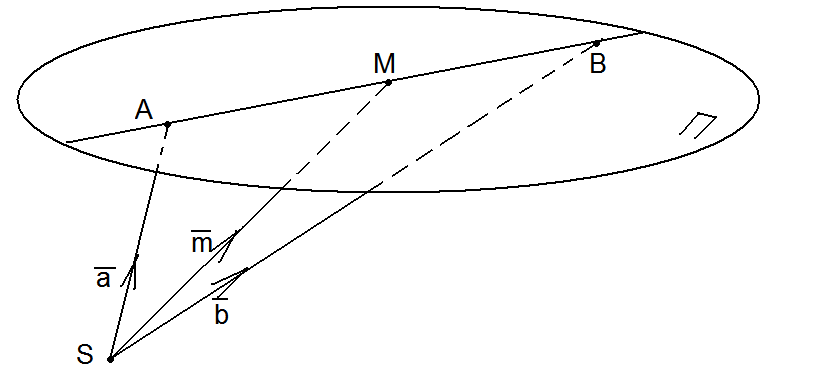
Пусть прямая l задана двумя различными точками А (а₁: а₂.: а₃) и В (b₁,: b₂: b₃). Найдём уравнение этой прямой в однородных координатах. Пусть М  произвольная точка и М (X:Y:Z). Если = { а₁, а₂., а₃},

= { b1,, b2, b3} = { X, У, Z}, то  А,  В,  М. Следовательно, М  l  , икомпланарны . Получили уравнение прямой,

Рис.91

проходящей через две точки, в однородных координатах. Используем другое необходимое и достаточное условие комланарности трёх векторов. Так как векторы инеколлинеарны, тоМ  l  , где и  - любые действительные числа. Отсюда получаем параметрические уравнения прямой, проходящей через две данные точки

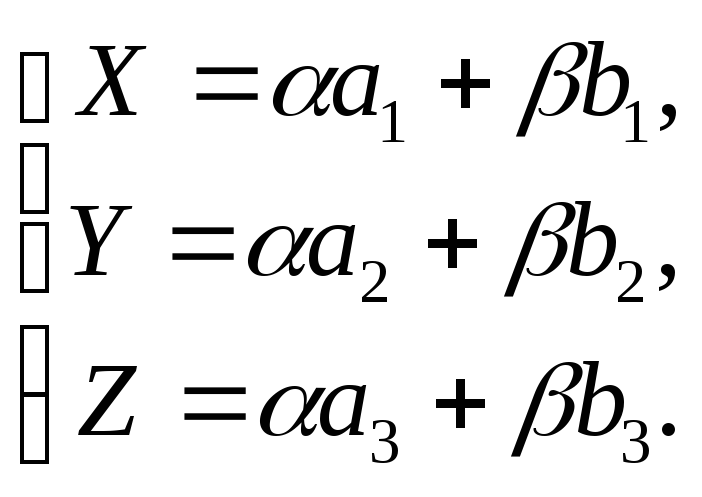
Здесь  и  любые действительные числа, не равные нулю одновременно.

Пусть М₀(X₀: Y₀: Z₀) – произвольная точка и l [U: V: W] – произвольная прямая, проходящая через М₀. Очевидно,

l  M₀  UX₀ + VY₀ + WZ₀ = 0.

Полученное уравнение называется уравнением точки.

Пусть l₁ [U₁: V₁: W₁] и l₂ [U₂: V₂: W₂] две различные прямые. Они пересекаются в некоторой точке М₀(X₀: Y₀: Z₀). Тогда

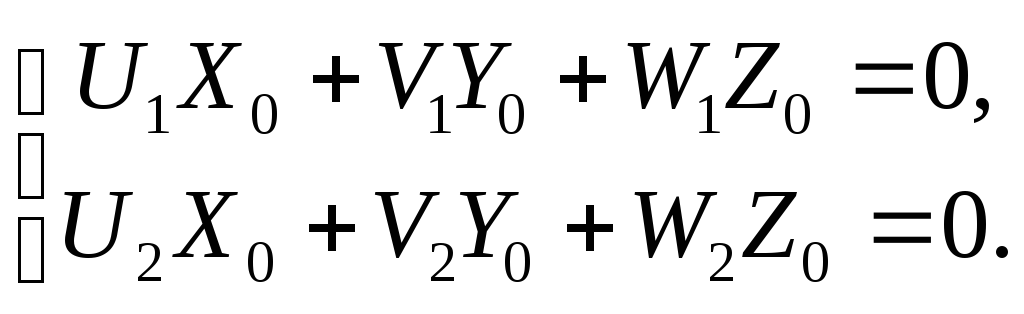
Коэффициенты в этих уравнениях не пропорциональны.

l  M₀  UX₀ + VY₀ + WZ₀ = 0.

Следовательно, система имеет ненулевое решение. но это возможно тогда и только тогда, когда её определитель равен нулю. Итак,

l  M₀ 

Получили уравнение точки, заданной двумя проходящими через неё прямыми. Так как векторы { U₁, V₁, W₁} и { U₂, V₂, W₂} линейно независимы, а вектор {U, V, W} с ними компланарен, то 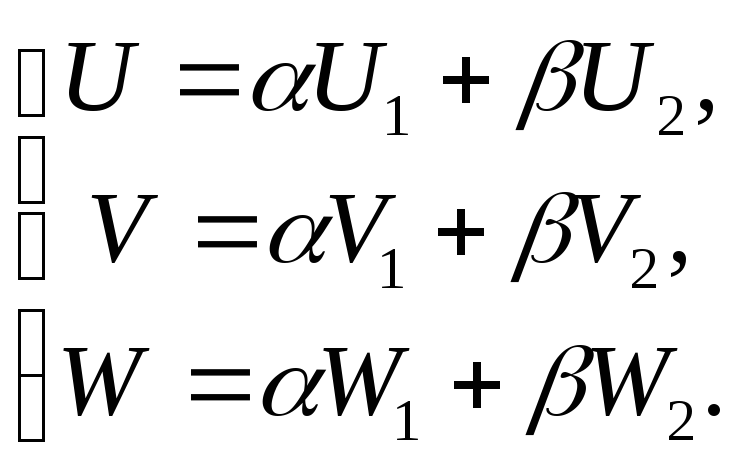Это параметрические уравнения точки.

Если линия второго порядка задана в аффинной системе координат уравнением а₁₁х² + 2а₁₂ху + а₂₂у² + 2а₁₃х + 2а₂₃у + а₃₃ = 0, то однородные координаты всех собственных точек этой линии будут удовлетворять уравнению а₁₁Х² + 2а₁₂ХУ + а₂₂У² + 2а₁₃XZ + 2а₂₃YZ + а₃₃Z² = 0. Итак, линия второго порядка в однородных координатах задаётся однородным уравнением второй степени от трёх переменных.

Пример 4. Эллипс, гипербола и парабола заданы в ПДСК каноническими уравнениями. Запишите их уравнения в соответствующих однородных координатах.

а) Пусть эллипс задан уравнением . Переходя к однородным координатам, получимили(*)

б) Пусть гипербола задана уравнением . Переходя к однородным координатам, получимили(**)

в) Пусть парабола задана уравнением у² = 2рх. Переходя к однородным координатам, получим илиУ²= 2рXZ. Если сделать преобразование координат X¹ = X + Z, Y¹ = Y, Z¹ = X  Z, то получим уравнение . (***)

Уравнения эллипса, гиперболы и параболы в однородных координатах однотипны, следовательно, это линии одного типа. Если Z = 0 (т.е. точка бесконечно удалённая), то из уравнения (*) Х = У = 0. Точек с такими координатами на расширенной плоскости нет (эллипс не имеет бесконечно удалённых точек). Из уравнения (**) при Z = 0 получим . Следовательно, на гиперболе две бесконечно удалённые точки (a : b : 0) и (a : b : 0). Но это бесконечно удалённые точки асимптот гиперболы. Из уравнения У²= 2рXZ при Z = 0 получим Y = 0. Следовательно, парабола имеет одну бесконечно удалённую точку (1 : 0 : 0).
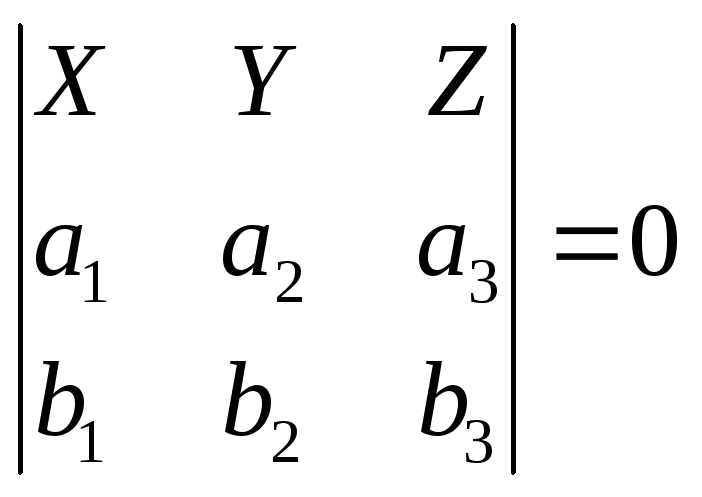