1.5. Компланарные векторы

Определение 8. Векторы называются компланарными, если их можно отложить в одной плоскости.

Свойства компланарных векторов.

1⁰. Коллинеарные векторы компланарны. Иными словами, во множество всех возможных компланарных между собой векторов вместе с каждым его вектором входят все векторы, коллинеарные с ним. В частности, нулевой вектор содержится в любом таком множестве и вместе с каждым вектором в это множество входит противоположный ему вектор. Отсюда же следует, что множество компланарных векторов замкнуто относительно операции умножения на действительное число.

2⁰. Сумма двух векторов есть вектор, компланарный с ними. Следовательно, множество компланарных векторов замкнуто относительно операции сложения.

3⁰. Три вектора компланарны тогда и только тогда, когда хотя бы один из них можно представить в виде линейной комбинации двух других.

Доказательство.  Пусть векторы компланарны. Возможны два случая.

1) Среди данных векторов есть хотя бы одна пара коллинеарных векторов. Пусть иколлинеарны. Тогда, по свойствам коллинеарных векторов, хотя бы один из них можно выразить через другой. Пусть. Тогда, т.е. векторесть линейная комбинация векторови.

2) Данные векторы попарно не коллинеарны. Отложим их от одной точки О. Пусть ,,. Отрезки ОА, ОВ, ОС попарно не параллельны. Проведём СD ОА так, что D  ОВ (прямой ОВ). Тогда получим , т.е. векторесть линейная комбинация векторови.

Рис. 9

 Пусть . По свойствам 1⁰ и 2⁰ следует, что вектор компланарен с векторамии.

4⁰. Если векторы ине коллинеарны, то любой компланарный с ними вектор можно представить в виде их линейной комбинации.

Теорема 4. Множество всех компланарных векторов есть двумерное векторное пространство над полем действительных чисел. Базисом в нём является любая упорядоченная пара неколлинеарных векторов.

Доказательство следует из предыдущих свойств.

Задача 3. АВСD и AB₁C₁D₁  два произвольных параллелограмма.

Докажите, что векторы ,,параллельны одной плоскости. Решение. Для решения задачи достаточно показать, что эти векторы компланарны. ; ; = = () + () = =. Так как, то эти векторы компланарны .

Рис. 10

Теорема 5. Если векторы не компланарные, то любой геометрический вектор можно представить в виде их линейной комбинации.

Доказательство. Пусть векторы не компланарны. Очевидно, никакие два из них не являются коллинеарными. Пусть  любой вектор. Возможны два случая.

1) Вектор компланарен с какой-нибудь парой данных векторов. Пусть компланарен с векторами и . Тогда по свойству 3⁰ компланарных векторов .

2) Вектор не компланарен ни с одной парой данных векторов. Отложим все четыре вектора от одной точки О. пусть ,,и(рис. 11). Проведём (DM)  (M  (AOB)) и (MN)  (N  (OA)). Тогда . Ноколлинеарен вектору, поэтому. Аналогично,,. Следовательно,.

Рис. 11

Теорема 6. Множество всех геометрических векторов есть трёхмерное векторное пространство над полем действительных чисел. Базисом в нём является любая упорядоченная тройка некомланарных векторов.

Доказательство следует из теоремы 5 и свойств компланарных векторов.

В курсе линейной алгебры (в первом семестре) введены координаты вектора в данном базисе и рассмотрены свойства координат. Все определения и свойства их будут использоваться в векторных пространствах геометрических векторов.

Если в векторном пространстве зафиксированы два базиса В и В¹, Т – матрица перехода от базиса В к базису В¹, х и х¹ столбцы координат данного вектора в базисахВ и В¹ соответственно, то х = Тх¹. Если эти формулы переписать в координатах во множестве компланарных векторов, то получим

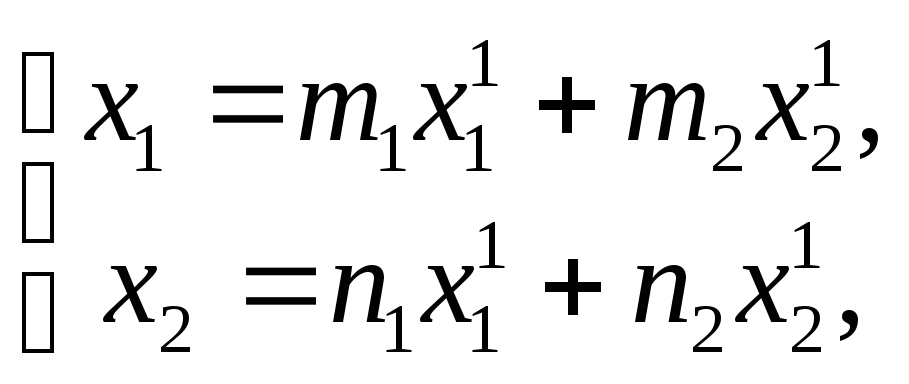где ,.

Во множестве всех геометрических векторов

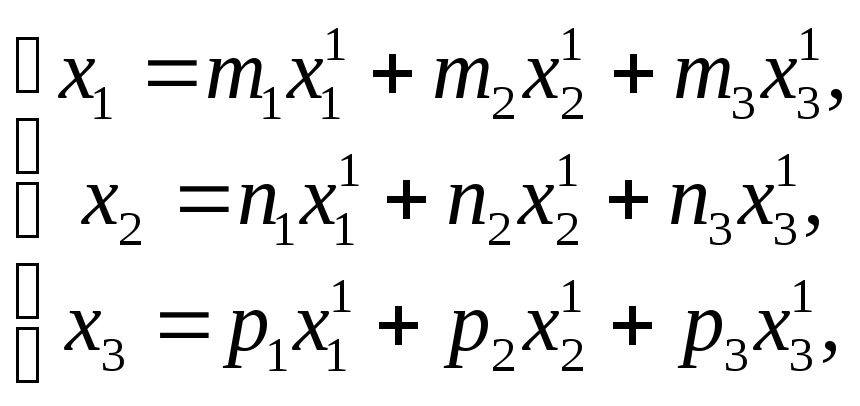где ,,