- •Аналитическая геометрия
- •I. Элементы векторной алгебры
- •1.1. Геометрические векторы
- •1.2. Сложение векторов
- •1.3. Умножение вектора на действительное число
- •1.4. Коллинеарные векторы
- •1.5. Компланарные векторы
- •1.6. Проекция на прямую параллельно данной плоскости
- •1.7. Проекция вектора на ось
- •1.8. Ортогональная проекция вектора на ось
- •1.9. Скалярное произведение векторов
- •1.10. Векторное произведение векторов
- •1.15. Смешанное произведение векторов
- •II. Метод координат на плоскости и в пространстве
- •2.1 Введение системы аффинных и прямоугольных координат на плоскости и в пространстве
- •2.2. Аффинные задачи на плоскости и в пространстве
- •2.2.1. Координаты вектора, заданного координатами его концов.
- •2.3. Метрические задачи на плоскости и в пространстве .
- •2.3.1. Расстояние между точками.
- •2.3.2. Угол, заданный тремя точками.
- •2.4. Преобразование аффинных координат на плоскости и в пространстве
- •2.5. Преобразование прямоугольных координат на плоскости
- •2.6. Полярные координаты на плоскости
- •2.7. Цилиндрические и сферические координаты в пространстве
- •III. Образы первой ступени
- •3.1. Условия, определяющие фигуру в системе координат
- •3.2. Прямая в аффинной системе координат на плоскости и в пространстве
- •3.2.1. Уравнения прямой, проходящей через данную точку параллельно данному вектору
- •3.2.2. Уравнения прямой, проходящей через две точки
- •3.2.3. Общие уравнения прямой
- •I.Общее уравнение прямой на плоскости
- •2. Общие уравнения прямой в пространстве
- •3.2.4. Исследование взаимного расположения прямых
- •3.3. Прямая в прямоугольной системе координат на плоскости
- •3.3.1. Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору
- •3.3.2. Уравнение прямой, проходящей через данную точку под данным углом к оси (Ох)
- •3.3.3. Нормальное уравнение прямой
- •3.3.4. Угол между двумя прямыми, заданными общими уравнениями
- •3.3.5. Угол между наклонными прямыми, заданными уравнениями с угловыми коэффициентами
- •3.3.6. Расстояние от точки до прямой
- •3.4. Пучок прямых на плоскости
- •3.6. Прямая и плоскость в пространстве
- •3.6.1. Плоскость в аффинной системе координат
- •3.6.1.1. Уравнения плоскости, проходящей через данную точку параллельно двум данным векторам
- •3.6.1.2.. Уравнения плоскости, проходящей через три данные неколлинеарные точки
- •3.6.1.3. Общее уравнение плоскости
- •3.6.1.4. Исследование взаимного расположения двух плоскостей
- •3.6.2. Плоскость и прямая в прямоугольной системе координат
- •3.6.2.1. Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору
- •3.6.2.2. Угол между двумя плоскостями
- •3.6.2.3. Угол между прямой и плоскостью
- •3.6.2.4. Расстояние от точки до плоскости
- •3.6.2.5. Расстояние от точки до прямой
- •3.6.2.6. Расстояние между скрещивающимися прямыми
- •IV. Образы второго порядка
- •4.1. Элементарная теория линий второго порядка
- •4.1.1. Окружность
- •4.1.2. Эллипс
- •4.1.3. Гипербола
- •4.1.4. Парабола
- •4.1.5. Эллипс, гипербола и парабола в полярных координатах
- •4.2. Упрощение уравнения линии второго порядка
- •4.2.1. Преобразование уравнения линии второго порядка при повороте прямоугольной системы координат
- •4.2.2. Упрощение уравнения линии второго порядка. Метрическая классификация линий второго порядка
- •4.3. Поверхности
- •4.3.1. Цилиндрические поверхности
- •4.3.2. Конические поверхности
- •4.3.3. Поверхности вращения
- •4.3.4. Эллипсоид
- •4.3.5. Однополостный гиперболоид
- •4.3.6. Двуполостный гиперболоид
- •4.3.7. Эллиптический параболоид
- •4.3.8. Гиперболический параболоид
- •4.3.9. Прямолинейные образующие поверхности
- •V. Расширенные евклидовы плоскость и пространство
- •5.1. Определение расширенных евклидовых плоскости и пространства
- •5.2. Однородные координаты на расширенной евклидовой плоскости
- •5.3. Уравнения прямой, точки и линий второго порядка в однородных координатах на расширенной евклидовой плоскости
- •5.4. Однородные координаты в расширенном евклидовом пространстве
- •5.5. Уравнения плоскости и прямой в однородных координатах
- •Задачи по аналитической геометрии для домашних заданий
- •Метод координат на плоскости и в пространстве
- •Lll. Прямая линия на плоскости
- •LV. Плоскость и прямая в пространстве
- •V. Элементарная теория кривых второго порядка
- •Vl. Элементарная теория поверхностей
- •Vll. Другие системы координат на плоскости и в пространстве
- •Основная литература
4.3. Поверхности
4.3.1. Цилиндрические поверхности
Пусть
Г
– линия и
![]() -
ненулевой вектор, не параллельный
плоскости линии Г
(если Г плоская
линия).
-
ненулевой вектор, не параллельный
плоскости линии Г
(если Г плоская
линия).
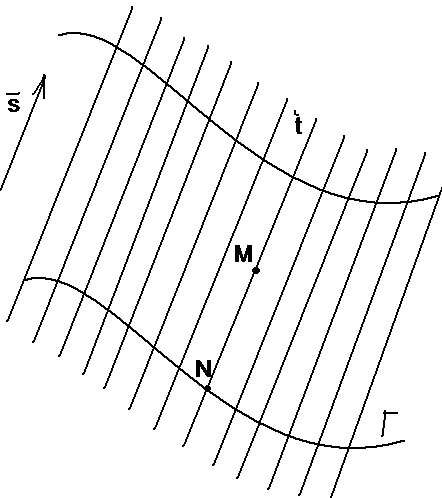
Определение
36.
Цилиндрической
поверхностью
с направляющей Г
и образующими, параллельными вектору
![]() ,
называется множество точек всех
возможных прямых, параллельных вектору
,
называется множество точек всех
возможных прямых, параллельных вектору
![]() и пересекающих линию
Г.
и пересекающих линию
Г.
Основная задача,
которую нужно решить: как найти уравнение
цилиндрической поверхности, если даны
уравнения линии Г
и координаты вектора
![]() .
.
|
Пусть в
пространстве введена АСК,
М
Ц
(М
l,
где l
||
Обозначим
l
Г
= N.
Если N(х0,
у0,
z0),
то
|
Рис. 78 |
![]() (86)
(86)
Остаётся из этих уравнений исключить параметр t.
Получили следующие правила для составления уравнения цилиндрической поверхности:
Если направляющая
цилиндрической поверхности задаётся
уравнениями (85) и образующие параллельны
вектору
![]() ,
то для составления уравнения поверхности
достаточно в уравнениях (85) заменить х
на х
mt,
у на у
nt,
z
на z
рt
и из полученных уравнений исключит
параметр.
,
то для составления уравнения поверхности
достаточно в уравнениях (85) заменить х
на х
mt,
у на у
nt,
z
на z
рt
и из полученных уравнений исключит
параметр.
Пример
1.
Составьте
уравнение цилиндрической поверхности,
если образующие параллельны вектору
![]() =3,
2, 1
и направляющая Г
имеет уравнения
=3,
2, 1
и направляющая Г
имеет уравнения
![]()
|
Решение. Линия Г – эллипс в плоскости (ХОУ) с полуосями 3 и 2 (рис. 79). В уравнениях линии Г заменяем х на х 3t, у на у 2t, z на z + t.
Получим
Из второго уравнения t = z. Подставим в первое уравнение. 4(х + 3z)2 + 9(у + 2z)2 = 36. Раскрыв скобки и приведя подобные, получим 4х2 + 9у2 + 72z2 + 24хz + 36уz 36 = 0. Это уравнение данной цилиндрической поверхности.
|
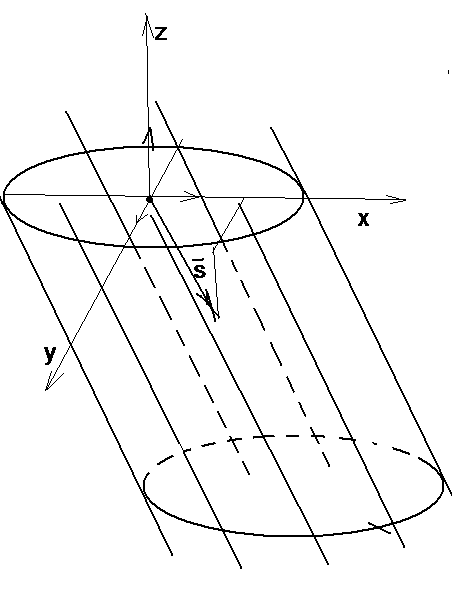
Рис.79 |
Пример
2.
Составьте
уравнение цилиндрической поверхности,
если направляющей является линия
![]() лежащая в плоскости (ХОУ),
а образующие параллельны оси (ОZ).
лежащая в плоскости (ХОУ),
а образующие параллельны оси (ОZ).
Решение.
Вектор, параллельный образующим, есть
вектор
![]() .
Заменяем в уравнениях направляющейх
на х
0•t,
т.е. х заменяем
на х.
Аналогично, у
заменяем на у.
Но z
заменяем на z
t. Получим
.
Заменяем в уравнениях направляющейх
на х
0•t,
т.е. х заменяем
на х.
Аналогично, у
заменяем на у.
Но z
заменяем на z
t. Получим
![]() Из второго уравненияz
= t. Это значит,
что z
может независимо от х
и у принимать
все возможные действительные значения,
а х
и у
связаны тем же уравнением f(х,у)
= 0, что и в уравнении направляющей.
Уравнение цилиндрической поверхности
в этом случае будет f(х,
у) = 0.
Из второго уравненияz
= t. Это значит,
что z
может независимо от х
и у принимать
все возможные действительные значения,
а х
и у
связаны тем же уравнением f(х,у)
= 0, что и в уравнении направляющей.
Уравнение цилиндрической поверхности
в этом случае будет f(х,
у) = 0.
Следствие.
Уравнения
![]() ,
,![]() ,у2
= 2рх задают
цилиндрические поверхности с направляющими
эллипсом, гиперболой и параболой
соответственно. Их образующие параллельны
оси (ОZ).
,у2
= 2рх задают
цилиндрические поверхности с направляющими
эллипсом, гиперболой и параболой
соответственно. Их образующие параллельны
оси (ОZ).
Если направляющая цилиндрической поверхности есть линия второго порядка, то поверхность называется цилиндром второго порядка.
Замечание. Обратите внимание на то, что уравнения f(х, у) = 0, f(х, z) = 0, f(у, z) = 0, задают на плоскостях (ХОУ), (ХОZ) и (УОZ) соответственно некоторые линии. Но в аффинной системе координат в пространстве они задают цилиндры с образующими, параллельными оси (ОZ), (ОУ) и (ОХ) соответственно.

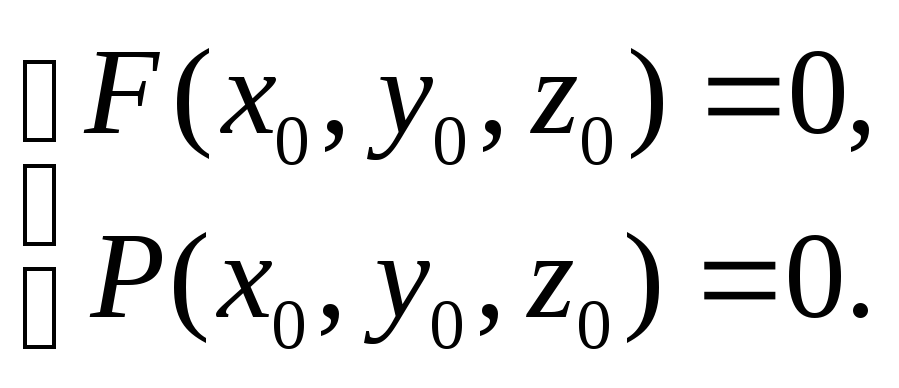 ()
Если М(х,
у, z), то
М
Ц
х = х0
+ mt, у = у0
+ nt, z = z0
+ рt, где t
R.
Отсюда х0
= х
mt, у0
= у
nt, z0
= z
рt. Подставив
х0,
у0,
z0
в равенства (),
получим уравнения Ц.
()
Если М(х,
у, z), то
М
Ц
х = х0
+ mt, у = у0
+ nt, z = z0
+ рt, где t
R.
Отсюда х0
= х
mt, у0
= у
nt, z0
= z
рt. Подставив
х0,
у0,
z0
в равенства (),
получим уравнения Ц.