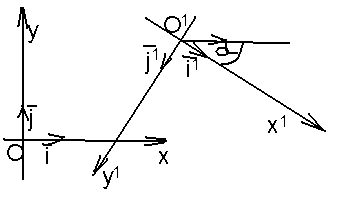- •Аналитическая геометрия
- •I. Элементы векторной алгебры
- •1.1. Геометрические векторы
- •1.2. Сложение векторов
- •1.3. Умножение вектора на действительное число
- •1.4. Коллинеарные векторы
- •1.5. Компланарные векторы
- •1.6. Проекция на прямую параллельно данной плоскости
- •1.7. Проекция вектора на ось
- •1.8. Ортогональная проекция вектора на ось
- •1.9. Скалярное произведение векторов
- •1.10. Векторное произведение векторов
- •1.15. Смешанное произведение векторов
- •II. Метод координат на плоскости и в пространстве
- •2.1 Введение системы аффинных и прямоугольных координат на плоскости и в пространстве
- •2.2. Аффинные задачи на плоскости и в пространстве
- •2.2.1. Координаты вектора, заданного координатами его концов.
- •2.3. Метрические задачи на плоскости и в пространстве .
- •2.3.1. Расстояние между точками.
- •2.3.2. Угол, заданный тремя точками.
- •2.4. Преобразование аффинных координат на плоскости и в пространстве
- •2.5. Преобразование прямоугольных координат на плоскости
- •2.6. Полярные координаты на плоскости
- •2.7. Цилиндрические и сферические координаты в пространстве
- •III. Образы первой ступени
- •3.1. Условия, определяющие фигуру в системе координат
- •3.2. Прямая в аффинной системе координат на плоскости и в пространстве
- •3.2.1. Уравнения прямой, проходящей через данную точку параллельно данному вектору
- •3.2.2. Уравнения прямой, проходящей через две точки
- •3.2.3. Общие уравнения прямой
- •I.Общее уравнение прямой на плоскости
- •2. Общие уравнения прямой в пространстве
- •3.2.4. Исследование взаимного расположения прямых
- •3.3. Прямая в прямоугольной системе координат на плоскости
- •3.3.1. Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору
- •3.3.2. Уравнение прямой, проходящей через данную точку под данным углом к оси (Ох)
- •3.3.3. Нормальное уравнение прямой
- •3.3.4. Угол между двумя прямыми, заданными общими уравнениями
- •3.3.5. Угол между наклонными прямыми, заданными уравнениями с угловыми коэффициентами
- •3.3.6. Расстояние от точки до прямой
- •3.4. Пучок прямых на плоскости
- •3.6. Прямая и плоскость в пространстве
- •3.6.1. Плоскость в аффинной системе координат
- •3.6.1.1. Уравнения плоскости, проходящей через данную точку параллельно двум данным векторам
- •3.6.1.2.. Уравнения плоскости, проходящей через три данные неколлинеарные точки
- •3.6.1.3. Общее уравнение плоскости
- •3.6.1.4. Исследование взаимного расположения двух плоскостей
- •3.6.2. Плоскость и прямая в прямоугольной системе координат
- •3.6.2.1. Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору
- •3.6.2.2. Угол между двумя плоскостями
- •3.6.2.3. Угол между прямой и плоскостью
- •3.6.2.4. Расстояние от точки до плоскости
- •3.6.2.5. Расстояние от точки до прямой
- •3.6.2.6. Расстояние между скрещивающимися прямыми
- •IV. Образы второго порядка
- •4.1. Элементарная теория линий второго порядка
- •4.1.1. Окружность
- •4.1.2. Эллипс
- •4.1.3. Гипербола
- •4.1.4. Парабола
- •4.1.5. Эллипс, гипербола и парабола в полярных координатах
- •4.2. Упрощение уравнения линии второго порядка
- •4.2.1. Преобразование уравнения линии второго порядка при повороте прямоугольной системы координат
- •4.2.2. Упрощение уравнения линии второго порядка. Метрическая классификация линий второго порядка
- •4.3. Поверхности
- •4.3.1. Цилиндрические поверхности
- •4.3.2. Конические поверхности
- •4.3.3. Поверхности вращения
- •4.3.4. Эллипсоид
- •4.3.5. Однополостный гиперболоид
- •4.3.6. Двуполостный гиперболоид
- •4.3.7. Эллиптический параболоид
- •4.3.8. Гиперболический параболоид
- •4.3.9. Прямолинейные образующие поверхности
- •V. Расширенные евклидовы плоскость и пространство
- •5.1. Определение расширенных евклидовых плоскости и пространства
- •5.2. Однородные координаты на расширенной евклидовой плоскости
- •5.3. Уравнения прямой, точки и линий второго порядка в однородных координатах на расширенной евклидовой плоскости
- •5.4. Однородные координаты в расширенном евклидовом пространстве
- •5.5. Уравнения плоскости и прямой в однородных координатах
- •Задачи по аналитической геометрии для домашних заданий
- •Метод координат на плоскости и в пространстве
- •Lll. Прямая линия на плоскости
- •LV. Плоскость и прямая в пространстве
- •V. Элементарная теория кривых второго порядка
- •Vl. Элементарная теория поверхностей
- •Vll. Другие системы координат на плоскости и в пространстве
- •Основная литература
2.5. Преобразование прямоугольных координат на плоскости
Пусть на плоскости
даны две системы прямоугольных координат,
заданные реперами R
=![]() иR1
=
иR1
=![]() ,О1(х0,
у0)R
и
,О1(х0,
у0)R
и
![]() (рис.
77).
(рис.
77).
|
Пусть М(х,
у)R
и М(х1,
у1
1) Реперы R
=
|
Рис. 24 |
одинаково
ориентированы. Так как
![]() пр
пр![]() ,
пр
,
пр![]() )
= (cos,
sin)
и
)
= (cos,
sin)
и
![]() пр
пр![]() ,
пр
,
пр![]() )
= (sin,
cos),
то формулы (63) будут иметь вид
)
= (sin,
cos),
то формулы (63) будут иметь вид
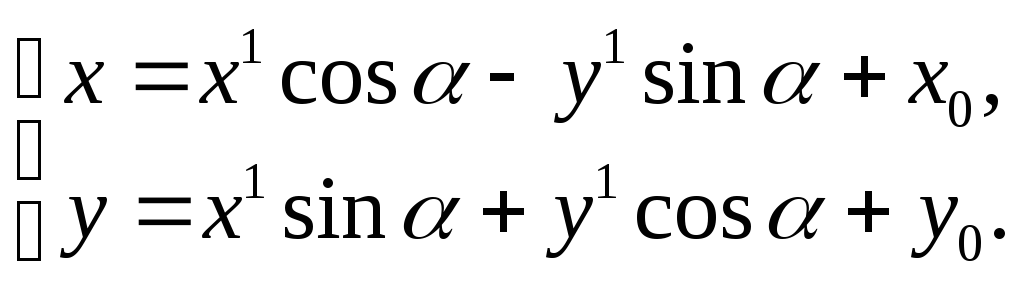 (64)
(64)
2) Реперы R
=
![]() иR1
=
иR1
=
![]() противоположно ориентированы (рис.24).
В этом случае формулы (63) примут вид
противоположно ориентированы (рис.24).
В этом случае формулы (63) примут вид
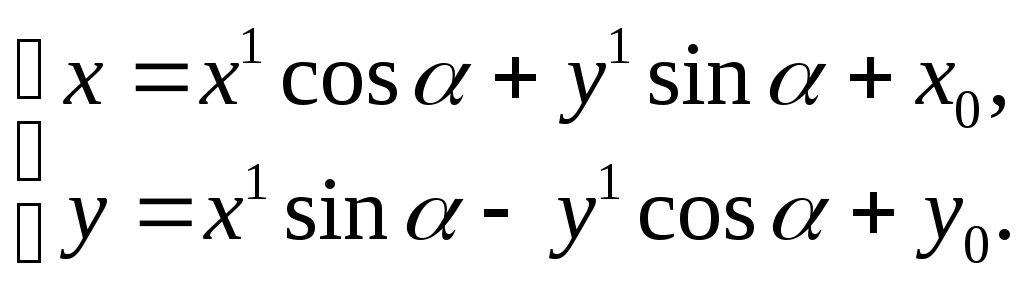 (65)
(65)
2.6. Полярные координаты на плоскости
Определение
18. Полярным
репером
называется совокупность фиксированных
точки и единичного вектора Р
=
![]() .
ТочкаО
называется
полюсом
(или началом полярной системы координат).
.
ТочкаО
называется
полюсом
(или началом полярной системы координат).
Точка О
вместе с вектором
![]() определяет луч, который называетсяполярной
осью.
определяет луч, который называетсяполярной
осью.
|
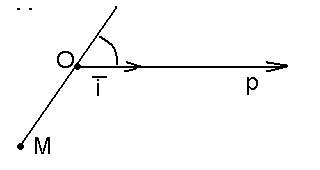
Пусть
М –
произвольная точка плоскости,
|
Рис. 25 |
и только одну. Но
любая точка плоскости имеет бесконечно
много пар полярных координат. Действительно,
если М (,
),
то М (,
+ 2к),
где к
– любое целое число. Точка О
– единственная
точка, для которой полярным углом может
быть любой угол. Полярный репер Р
=
![]() и ортонормированный реперR
=
и ортонормированный реперR
=
![]() называются соответствующими друг другу.
ЕслиМ (,
)Р
и М(х,
у)R,
то x
= cos,
y
= sin.
В полярных координатах
может
принимать все возможные действительные
значения, а
0. Если отказаться от условия, что
0, то мы получим обобщённые
полярные координаты.
называются соответствующими друг другу.
ЕслиМ (,
)Р
и М(х,
у)R,
то x
= cos,
y
= sin.
В полярных координатах
может
принимать все возможные действительные
значения, а
0. Если отказаться от условия, что
0, то мы получим обобщённые
полярные координаты.
Пусть М (, ). Если 0, то обобщенные полярные координаты совпадают с обычными полярными координатами. Если же 0, то точка М определяется так: проведём луч под углом к полярной оси и
|
на дополнительном к нему луче отложим отрезок ОМ, длина которого равна || (рис. 26).
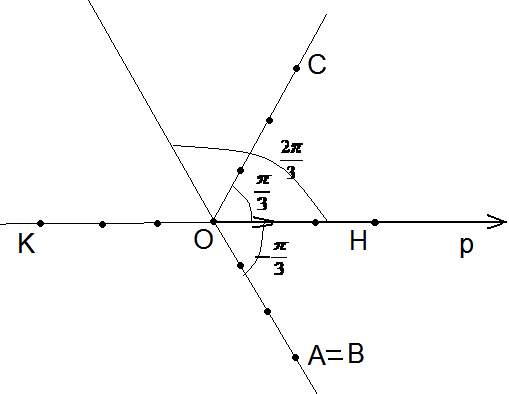
Задача
13. Постройте
точки, заданные в полярной системе
координат А(3,
|
Рис. 26 |
|
Решение.
Для построения точки А
проводим луч с началом в точке О
под углом |
Рис. 27 |
откладываем от
точки О
отрезок длины 3
= 3, получаем , что В
= А.
Для построения точки С
проводим
луч под углом
![]() к полярной оси и на нём откладываем
отрезок длины 3. ЛучОК
образует с осью угол
и имеет
длину 3. Луч ОН
сонаправлен
с осью и имеет длину 3.
к полярной оси и на нём откладываем
отрезок длины 3. ЛучОК
образует с осью угол
и имеет
длину 3. Луч ОН
сонаправлен
с осью и имеет длину 3.
Пусть полярная
система координат задана репером Р
=
![]() ,
а прямоугольная система координат
задана реперомR
=
,
а прямоугольная система координат
задана реперомR
=
![]() (т.е.
начало координат у них одно и то же и
полярная ось совпадает с осью абсцисс).
ПустьМ
– произвольная точка плоскости, М
(,
)Р
и М (х,
у)R.
Так как х
= пр
(т.е.
начало координат у них одно и то же и
полярная ось совпадает с осью абсцисс).
ПустьМ
– произвольная точка плоскости, М
(,
)Р
и М (х,
у)R.
Так как х
= пр![]() и у =
пр
и у =
пр![]() ,
то
,
то
![]() Из этих формул следует, что
Из этих формул следует, что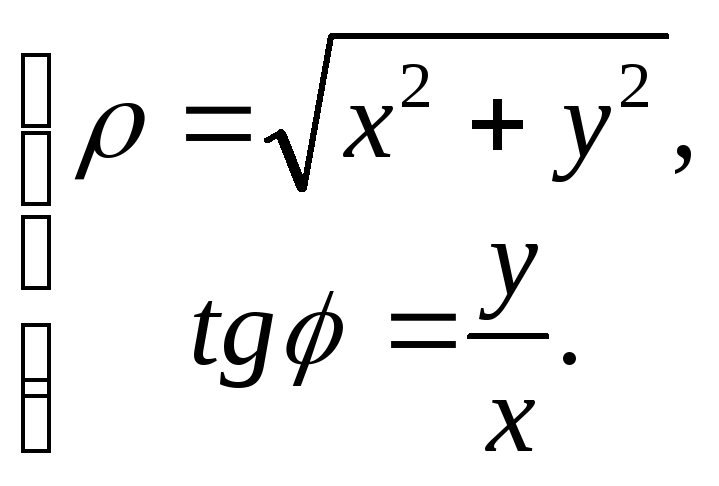 Получили связь между прямоугольными
декартовыми координатами точки иеё
соответствующими полярными координатами.
Получили связь между прямоугольными
декартовыми координатами точки иеё
соответствующими полярными координатами.