Аналитическая геометрия

(для направления «Прикладная математика и информатика)

I. Элементы векторной алгебры

1.1. Геометрические векторы

Определение 1. Геометрический отрезок называется ориентированным, если указан порядок его концов.

Определение 2. Геометрическим вектором (вектором) называется ориентированный отрезок. При этом начало и конец ориентированного отрезка называются соответственно началом и концом вектора. Длина ориентированного отрезка называется длиной вектора.

Вектор обозначается , гдеА – начало, а В – конец вектора. Если начало и конец вектора нас не интересуют, то вектор обозначают . Длина вектора обозначаетсяили. Если начало и конец вектора совпадают, то вектор называютнулевым и обозначают . Если начало и конец вектора – различные точки (А  В), то существует и только один луч с началом А, проходящий через точку В. Этот луч задаёт в пространстве направление, которое называется направлением данного вектора. Нулевой вектор не имеет направления.

Определение 3. Два вектора называются равными, если они либо оба нулевые, либо имеют одинаковые длину и направление.

Равенство векторов обладает следующими очевидными свойствами: 1) рефлексивность (всякий вектор равен сам себе); 2) симметричность ( если , то); 3)транзитивность (если и, то).

Множество всех равных векторов можно задать 1) одним из векторов (ориентированным отрезком); 2) упорядоченной парой точек; 3) длиной и направлением (в случае ненулевого вектора).

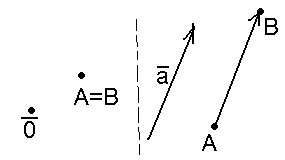
Пусть даны вектор и точка А. Если, то существует и только один вектор с началом в точкеА, равный данному вектору. Это вектор (т.е.В = А). Если , то существует и только один луч, сонаправленный с вектором. На этом луче существует и только одна точка В, расстояние от которой до точкиА равно . Но тогда

Рис. 1

А равно . Но тогда(рис. 1). Будем говорить, что векторотложен от точки А. Итак, любой вектор можно отложить от любой точки и только единственным образом.

Замечание. Часто бывает удобно все равные векторы считать за один вектор. В этом случае можно определить равенство ориентированных отрезков. Это равенство будет отношением эквивалентности на множестве всех ориентированных отрезков. Следовательно, множество ориентированных отрезков будет разбиваться на классы эквивалентности. Определение 2 можно дать в следующем виде.

Определение 2¹. Геометрическим вектором называется класс ориентированных отрезков. При этом каждый отрезок из класса называется изображением вектора (слово «изображение» часто опускают).

1.2. Сложение векторов

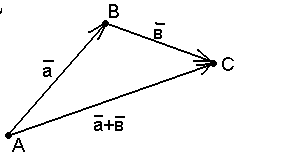
Пусть и любые два вектора. Чтобы к вектору прибавить векторнужно отложить векторот любой точки А (), от конца В полученного вектора отложить вектор(). Тогда векторбудетвектором суммы, т.е. . Иными словами, . Свойства сложения векторов.

Рис. 2

1⁰. Для любых двух векторов их сумма определена и однозначна. (Следует из определения).

2⁰. =для любого вектора. (Докажите).

3⁰. Для любого вектора существует противоположный вектор () такой, что+ () =. (Докажите).

4⁰. для любых векторови.

Доказательство. В случае, когда хотя бы один из векторов нулевой, утверждение следует из предыдущего свойства. Остаётся рассмотреть ненулевые векторы. При этом возможны следующие случаи.

а) Векторы ине параллельны. Пусть+=. Отложим от точки А вектор, пусть. Так какиимеют одинаковые длины и направления, то АВСD – параллелограмм. Следовательно, отрезки АВ и DC тоже имеют одинаковые длины и направления. Итак, . По правилу сложения векторов

Рис. 3

и . Отсюда.

б) Векторы ипараллельны и одинаково направлены (сонаправлены). В этом случае при откладывании от точки А получим,(рис.4). Векторыисонаправлены с вектором,

Рис. 4

поэтому сонаправлены между собой. Очевидно, . Следовательно,, т.е..

в) Случай, когда векторы ипараллельны и противоположно направлены, рассмотрите самостоятельно.

Определение 4. Векторы называются коллинеарными, если их можно отложить на одной прямой.

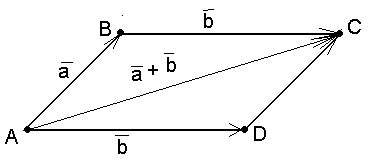
Очевидно, два вектора неколлинеарны тогда и только тогда, когда они ненулевые и не параллельные. Из случая а) проведённого доказательства следует ещё одно правило сложения неколлинеарных векторов:

Чтобы сложить два неколлинеарных вектора, достаточно отложить их от одной точки, построить на них, как на сторонах, параллелограмм, тогда диагональ этого параллелограмма, идущая из данной точки, будет задавать вектор суммы.

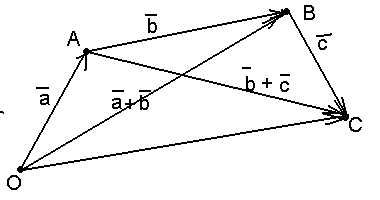
50. для любых векторов Доказательство. Для левой части получим . Для правой части . Итак, результаты равны. Из свойств 10 – 50 вытекает

Рис. 5

Теорема 1. Множество всех геометрических векторов есть аддитивная абелева группа.

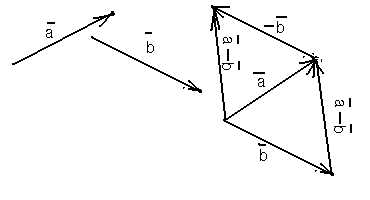
Определение 5. Разностью упорядоченной пары векторов называется сумма первого вектора и вектора, противоположного второму, т.е.

.

Чтобы вычесть из одного вектора второй, достаточно отложить оба вектора от одной точки. Тогда вектор, соединяющий концы полученных отрезков и направленный в сторону уменьшаемого, будет вектором разности (рис. 6). Очевидно, это правило не зависит от того, будут ли векторы коллинеарными или неколлинеарными. Свойства разности:

Рис. 6

1⁰. Для любой упорядоченной пары векторов их разность определена и однозначна.

2⁰. Разность двух векторов антикоммутативна.

для любых векторов и.

3⁰. Не выполняется ассоциативный закон, а именно

для любых векторов ,и.

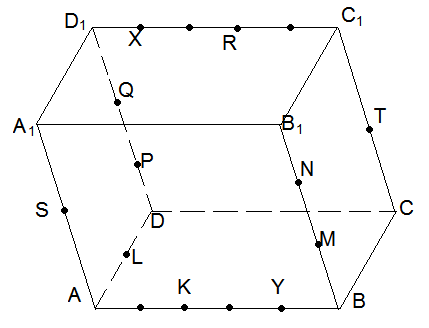
Задача 1. АВСDA₁B₁C₁D₁  параллелепипед, =,,,

, ,, . Найдите 1) ; 2). Решение. 1) Так как ,,, то=+++=. 2) Так как и, то = .

Рис. 7