
Boyarshinov_ChM_T2
.pdf
Аппроксимация уравнения разностной схемой. Порядок аппроксимации
Краевую задачу в общем случае можно записать в форме:
Au f 0, |
x G, |
|
|
||||||
|
|
|
|
|
|
|
|
|
(4.19) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x G. |
|
|
|
Ru 0, |
|
|
|||||||
Здесь в качестве аргумента x выступает вектор x |
t, x1, x2 , , xn . Область |
||||||||
G G |
покрывается сеткой , состоящей из граничных |
и внутренних |
|||||||
|
узлов. Задача (4.20) заменяется разностным аналогом |
|
|||||||
A u |
h |
f |
h |
0, |
x , |
|
|
||
|
h |
|
|
|
|
|
(4.20) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x . |
|
|
Rhuh h 0, |
|
|
|||||||
Близость разностной схемы к исходной задаче определяется величинами
невязок
h Ahu fh , |
x , |
h Rhu h , |
x , |
получаемых после подстановок точного решения в разностные аналоги дифференциального оператора и краевых условий. Очевидно, что чем меньше величина невязки, тем точнее разностная схема аппроксимирует исходную задачу.
Разностная схема (4.20) аппроксимирует задачу (4.19), если
|
h |
0 |
, |
|
h |
0 |
. |
|
h 0 |
|
h 0 |
Аппроксимация имеет порядок p, если
h |
O hp , |
h |
O hp . |
Пример 4.1. Оценим порядок аппроксимации уравнения (4.2) разностной схемой (4.16):
i |
q ti 1 |
,xj q ti |
,xj |
q ti |
,xj 1 2q ti ,xj q ti |
,xj 1 |
|
. |
|
|
|
|
h2 |
|
|
||
j |
|
|
|
|
|
|
Подставим разложения функции t,x в ряды Тейлора возле точки ti,xj
q ti 1 ,xj q ti |
,xj q˙ ti |
,xj q˙˙ ti |
,xj 2 |
O 3 , |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
3 |
|
|
|
|
q ti ,xj 1 q ti |
,xj q ti |
,xj h q ti ,xj h2 |
q ti ,xj h6 |
|
|
|
|
||
|
|
|
|
|
qiv ti ,xj h4 |
qv ti ,xj |
h5 |
O h6 , |
|
|
|
|
|
|
|
24 |
|
120 |
|
98

|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
q ti ,xj 1 q ti |
,xj q ti |
,xj h q ti |
,xj h2 |
q ti ,xj h6 |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
qiv ti ,xj |
h4 |
qv ti ,xj |
h5 |
O h6 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24 |
|
|
120 |
|
|
в формулу невязки: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
q˙ |
t |
,x |
q˙˙ t |
,x |
|
2 |
|
|
|
q |
t |
,x |
h2 qiv |
t |
,x |
|
h4 |
|
|
|
|||||||||
|
|
|
|
|
|
j 12 O h4 |
|
|
|||||||||||||||||||||
ij |
i |
|
j |
|
i |
|
j |
|
2 O 2 |
i |
|
j |
|
h2 |
|
i |
|
|
|
|
|||||||||
q˙ ti ,xj q˙˙ ti |
,xj |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
q ti ,xj qiv ti ,xj h |
|
O 2 O h4 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
qiv ti ,xj h |
2 |
|
|
|
|
|
|
|
|
|
|
||||||
q˙ ti ,xj q ti ,xj q˙˙ ti ,xj |
|
O 2 h4 . |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Выражение в первых скобках соответствует дифференциальному |
|||||||||||||||||||||||||||||
уравнению (4.2) и обращается в нуль. Оставшиеся слагаемые |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
qiv ti ,xj h |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ij q˙˙ ti ,xj |
|
O 2 h4 O h2 |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
определяют величину погрешности аппроксимации, имеющую для рассматриваемой разностной схемы первый порядок относительно шага по времени и второй относительно шага по координате. Очевидно, что это утверждение имеет место при малых шагах интегрирования t и h, а также ограниченных значениях второй производной q˙˙ ti ,xj по времени и четвертой производной qiv ti ,xj по координате.
Дополнительно произведем выкладки:
q˙˙ |
2q |
q |
|
|
2q |
|
|
2 |
q |
|
|
2 |
|
2q |
|
4q |
2qiv , |
|
|
|
|||||||||||||||||||||
t |
2 |
t t |
|
x |
2 |
|
x |
2 |
|
|
x |
2 |
|
x |
2 |
2 |
x |
4 |
|
|
|
||||||||||||||||||||
|
|
|
|
t |
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
i |
2 iv |
i |
|
j |
|
|
iv |
|
i |
|
j |
h2 |
|
|
2 |
|
4 |
|
|
|
|
iv |
|
|
i |
|
|
|
|
h2 |
|
2 4 |
. |
|
||||||
|
j |
|
|
,x |
q |
|
,x |
|
|
|
|
|
|
q |
|
|
,x |
j |
|
|
|
|
|
||||||||||||||||||
|
q |
|
t |
|
|
|
t |
|
12 |
O h |
|
|
|
|
|
t |
|
6 |
O h |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Если установить между шагами интегрирования соотношение |
h2 |
, в |
|||||||||||||||||||||||||||||||||||||||
последнем выражении сохраняются лишь слагаемые |
|
|
|
|
|
|
|
|
|
6 |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
ij |
O 2 h4 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
второго порядка малости по |
|
|
и четвертого по h, то есть порядок |
||||||||||||||||||||||||||||||||||||||
аппроксимации удалось существенно повысить. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
При использовании начальных условий (4.3) и граничных условий (4.4) погрешность аппроксимации отсутствует, поскольку узловые значения искомой
99
функции в начальный момент и в граничных точках задаются точно. При использовании граничного условия второго рода (4.5) производная по координате также заменяется разностным аналогом, например
qin qin 1 q(t ).
h
Для оценки погрешности аппроксимации граничного условия воспользуемся разложением в ряд функции q t,x вблизи точки xn :
q ti ,xN 1 q ti ,xN q ti ,xN h O h2 ,
iN qiN qiN 1 q(t ) q ti ,xN O h q(t ) q ti ,xN q(t ) O h . h
Поскольку согласно условию (4.5) имеет место соотношение
q ti ,xn q(t),
погрешность аппроксимации граничного условия рассмотренным разностным аналогом имеет первый порядок (ниже порядка аппроксимации самого дифференциального уравнения). В результате вся разностная задача будет иметь также первый порядок аппроксимации.
Для повышения порядка аппроксимации воспользуемся разложением решения в ряд Тейлора:
q ti |
,xN 1 q ti ,xN q ti |
,xN h q ti |
,xN h2 |
O h3 . |
|
|
|
2 |
|
Подставим в это выражение уравнение (4.2) и граничное условие (4.5):
q ti ,xN 1 q ti ,xN q ti h q˙ ti ,xN |
h2 |
3 |
. |
2 O h |
|
На основе этого соотношения построим явный разностный аналог граничного условия (4.5)
qiN 1 |
qiN |
h2 |
qi 1 |
qi |
, |
(4.21) |
qi h |
N |
N |
||||
|
|
2 |
|
|
|
|
имеющий второй порядок аппроксимации.
Неявная схема для граничного условия (4.5) имеет вид:
qiN11 qiN1 qi 1h h2 qiN1 qiN .
2
Устойчивость разностных схем
Понятие устойчивости предполагает получение оценки развития возмущения, внесенного на каком-либо этапе расчетов, с увеличением числа шагов интегрирования.
100

Разностная схема19 (4.20) |
устойчива, если |
0 |
, |
не зависящее от |
|
шага интегрирования h, что |
u1 u2 если f1 |
f2 , |
1 |
2 . |
|
При численном интегрировании многомерных дифференциальных уравнений шаги по разным переменным могут быть различными. В этом случае устойчивость называется безусловной, если приведенное определение устойчивости имеет место для любых малых шагов. Устойчивость считается условной, если шаги по разным координатам должны удовлетворять дополнительным соотношениям.
Непрерывная зависимость решения дифференциального уравнения от функции f называется устойчивостью по правой части.
Непрерывная зависимость решения дифференциального уравнения от называется устойчивостью по краевым условиям.
Устойчивость по краевому условию t t0 называется устойчивостью по начальным данным.
В дальнейшем рассматриваются, как правило, двухслойные по времени разностные схемы, поскольку дифференциальные уравнения n-го порядка могут быть заменены системой n уравнений первого порядка, каждое из которых требует для аппроксимации только два временных слоя (два близких момента времени). В дальнейшем для упрощения записей разностных выражений будут использоваться следующие обозначения:
символ |
(острие стрелки вверх) соответствует значению функции на |
||
следующем |
временном слое, |
uj uij 1 |
- численное значение функции в |
координатном узле xj, временном слое ti+1; |
|||
символ |
(острие стрелки вниз) соответствует значению функции на |
||
предыдущем временном слое, то есть uj |
uij 1; |
||
отсутствие символов |
или |
соответствует значению функции на |
|
текущем временном слое, то есть uj uij .
Двухслойная разностная схема называется равномерно устойчивой по начальным данным, если она равномерно устойчива по аргументу t:
u1 t u2 t K u1 t0 u2 t0 |
t 0,T , |
|
K>0 |
- постоянная, не зависящая от величин t и h. |
|
u1(t, x), u2(t, x) |
- решения задачи (4.20) с разными начальными |
|
условиями и одной и той же правой частью.
19 Согласно [13], “... схема численно неустойчива, если приводит к возникновению хаотических решений, не имеющих отношения к решению дифференциального уравнения. Такое поведение подчеркивает различие между точными конечно-разностными аналогами для производных и точным аналогом дифференциального уравнения”.
101
Теорема 4.1 (признак равномерной устойчивости).
Если |
Ahu1 Ahu2 , то для равномерной устойчивости по начальным данным |
||||||||||||||
достаточно, чтобы при всех значениях i |
выполнялось соотношение |
||||||||||||||
u1 |
u2 |
|
1 |
|
C |
|
u1 |
|
u2 , |
|
ti 1 |
|
ti , C |
|
0. |
|
|
|
|
|
|
|
|
|
|||||||
Доказательство. В силу допущения теоремы Ahu1 Ahu2 возмущение правой части уравнения (4.20) отсутствует. Формула теоремы означает, что при
наличии погрешности u u1 |
u2 |
на временном слое ti, для следующего момента |
|||||||||||||||||
времени ti+1 норма возмущения |
u |
u1 u2 |
возрастет не более чем в (1 + Ct) |
||||||||||||||||
раз. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Учитывая, что имеет место оценка |
|
1 C eC , можно оценить величину |
|||||||||||||||||
погрешности за произвольное число m t t0 |
|
шагов по времени: |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u e |
C |
e |
C |
u |
0 |
e |
Cm |
u |
0 |
e |
C t t0 |
u |
0 |
e |
C T t0 |
|
u |
0 . |
|
|
|
|
|
|
|
||||||||||||||
14243 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
m
Обозначим K eC T t0 , тогда t t0 ,T имеет место
 u
u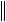 K
K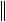 u0
u0 ,
,
то есть выполняется определение равномерной устойчивости. Что и требовалось доказать.
Теорема 4.2 (признак устойчивости по правой части).
Двухслойная разностная схема устойчива по правой части, если она устойчива по начальным данным и такова, что если два разностных решения Ahu1 f1, Ahu2 f2 равны на некотором слое, u1 u2 , то на следующем слое выполняется соотношение
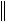 u1 u2
u1 u2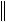
 f1 f2
f1 f2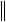 , const .
, const .
Доказательство. |
Пусть |
~ |
- решение разностного уравнения (4.20) с |
|
u |
||||
возмущенной правой частью: |
|
|
||
~ |
~ |
|
|
|
Ahu |
f . |
|
|
|
Поскольку возмущения начальных данных нет, имеет место |
||||
u 0,x |
~ |
|
|
|
u 0,x . |
|
|
|
|
Для доказательства построим последовательность вспомогательных |
||||
функций vk , k 0,M |
следующим образом. |
|||
Пусть функция v0(t, x) совпадает с невозмущенным решением u(t, x) задачи (4.20). Функция v1(t, x) (рис. 4.2) представляет собой решение разностного уравнения
102
~ |
, t t |
, |
||
f |
|
|||
Ahv1 |
1 |
|
1 |
|
f |
, |
t t1, |
||
в котором правая |
часть возмущена только на отрезке t0 ,t1 , с начальным |
|||
условием |
|
|
|
|
v1 t0 ,x v0 t0 ,x .
Функция v2(t, x) - решение разностного уравнения
~
Ahv2 f2 , t t2 ,f , t t2 ,
но при возмущенной правой части на отрезке t0 ,t2 , причем в качестве начального условия принимается
v2 t1 ,x v1 t1 ,x ,
поскольку очевидно, что имеет место равенство
v1 t,x v2 t,x , t t0 ,t1 .
Аналогичным образом функция v3(t, x) определяется как решение задачи
~ |
, |
t t |
|
, |
|
f |
|
|
|||
Ahv3 |
3 |
|
|
3 |
. |
f |
, |
t t3 , |
|||
на отрезке t0,t3 с начальными условиями v3 t2 ,x v2 t2 ,x .
v 0
= u
v1 v2 v3
~
vM u
t0 |
t1 |
t2 |
t3 |
... |
tm |
tm+1 |
tM |
Рис. 4.2. Схема построения последовательности функций vk
Для произвольного номера m
103
~ |
, t t |
|
, |
|
|
|
f |
|
|
,x vm 1 tm 1 |
,x . |
||
Ahvm |
m |
|
m |
vm tm 1 |
||
f |
, |
t tm , |
|
|
||
Понятно, что последняя функция этой последовательности совпадает с решением задачи (4.20) с правой частью, возмущенной на всем отрезке интегрирования, то есть
~ |
t,x , |
t 0,T . |
vM t,x u |
Рассмотрим две функции vm(t,x) и vm+1(t,x) на отрезке построения значения этих функций в точке tm совпадают,
следовательно (в соответствии с условием теоремы) имеет место соотношение:
|
~ |
|
|
|
|
|
vm 1 tm 1 vm tm 1 fm f . |
|
|
|
|
|
|
При |
t tm 1 правые части |
разностных |
схем |
Ahum f |
и |
Ahum 1 f |
совпадают; |
значения функций |
vm 1 tm 1 ,x , |
vm tm 1 ,x |
различны. |
Это можно |
|
трактовать как различие в начальных данных для краевой задачи. Согласно признаку равномерной устойчивости имеет место оценка
vm 1 T vm T |
K vm 1 tm 1 vm tm 1 |
~ |
f . |
K fm |
|||
Отсюда получаем: |
|
|
|
~ |
v0 T vM T v0 T vM T v1 |
T v1 T v2 T v2 T |
|
u T u T |
|||
 v0 T v1 T
v0 T v1 T 
 v1 T v2 T
v1 T v2 T 
M 1 ~ |
f . |
K fk |
M 1
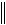 vM 1 T vM T
vM 1 T vM T 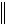
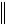 vk T vk 1 T
vk T vk 1 T 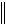
k 0
k 0
Учитывая, что
~ |
~ |
|
|
fk f |
f |
f , k 0,M 1, |
|
окончательно получаем: |
|
||
~ |
|
~ |
~ |
u T u T |
K M f f K T t0 |
f f . |
|
Если положить K T t0 , то из условия
~
f f
следует
~ |
T , |
u T u |
то есть определение устойчивости разностного решения по правой части. Что и требовалось доказать.
104

Необходимо подчеркнуть, что устойчивость по правой части не может рассматриваться независимо от устойчивости по начальным данным.
Принцип максимума
Теперь сформулируем условия для конструктивной оценки устойчивости разностных схем. Обратимся к алгебраическим уравнениям неявной разностной схемы дифференциального уравнения теплопроводности:
|
|
|
|
|
1 |
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|||||
q j 1 |
|
|
2 |
q j |
|
|
2 |
|
q j 1 |
|
h |
2 |
|
q j . |
|
|
|
|
||||
|
|
h |
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Это соотношение условно можно записать в виде |
||||||||||||||||||||||
kqk |
pq p |
f j , |
|
|
|
|
|
|
|
|
|
|
|
|
(4.22) |
|||||||
k |
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где для рассматриваемого случая |
|
k |
пробегает значения j-1, j, j+1; p = j, а |
|||||||||||||||||||
коэффициенты принимают значения |
|
|
|
|
|
|
|
|||||||||||||||
j 1 |
|
|
j |
1 |
2 |
, |
j 1 |
|
|
j |
1 |
; |
||||||||||
|
2 , |
|
|
|
2 |
|
h |
2 |
, |
|
||||||||||||
|
|
|
h |
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
||||
правая часть f j 0.
Положим
|
max |
max |
k . |
|
|
|
|
|
|
|
k |
|
|
|
|
|
|||
Для указанного разностного уравнения max |
|
1 |
2 |
||||||
|
|
h |
2 |
. |
|||||
|
|
|
|
|
|
|
|
||
Теорема 4.3 (принцип максимума). Разностная схема равномерно |
|||||||||
устойчива по начальным данным, если |
|
|
|
|
|
||||
max |
k |
p . |
|
|
|
|
(4.23) |
||
|
|
k max |
|
p |
|
|
|
|
|
Разностная схема устойчива по правой части, если выполнено условие |
|||||||||
(4.23) и имеет место |
|
|
|
|
|
||||
max |
k |
, 0. |
|
|
|
|
(4.24) |
||
|
|
k max |
|
|
|
|
|
|
|
Доказательство. Внесем возмущение dq в решение задачи (4.20) на исходном временном слое; возмущение правой части отсутствует.
Выражение (4.22), записанное для погрешности,
kqk pq p ,
k p
представим в форме
maxqmax pq p kqk .
p |
k max |
105

Оценим слагаемые последнего выражения по модулю:
max |
|
p |
q p |
|
k |
|
qmax |
qk . |
|||||
|
|
p |
|
|
k max |
|
Полученное неравенство справедливо для всех внутренних узлов разностной сетки, втом числе и для того узла, в котором погрешность q достигает наибольшего значения. С использованием чебышевской нормы
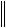 q
q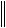 max
max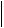 qk
qk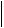
k
преобразуем предыдущее выражение:
max |
|
p |
q p |
|
k |
|
q |
qk . |
|||||
|
|
p |
|
|
k max |
|
Усилим неравенство, заменяя все величины q p , qk наибольшими по всем узлам сетки значениями и используя определение чебышевской нормы:
max |
|
|
q p |
|
|||
q |
q k , |
||||||
|
|
|
|
|
p |
|
k max |
|
|
max |
|
|
|
|
q p . |
q |
k |
||||||
|
|
|
|
k max |
|
|
p |
Согласно условию (4.23)
p |
max |
|
k |
|
max |
|
|
|
|
k , |
|||||||
p |
|
|
k max |
|
|
|
k max |
|
что позволяет преобразовать полученное неравенство к виду
|
|
max |
|
|
|
q |
|
max |
|
|
|
, |
q |
k |
|
k |
|||||||||
|
|
|
|
k max |
|
|
|
|
|
k max |
|
|
откуда следует условие равномерной устойчивости по начальным данным:
|
q 1 C q , C 0. |
q |
Следует заметить, что множитель (1 + Ct) обычно включается в условие
(4.23)
1 C max |
|
k |
p |
(4.25) |
|
|
k max |
p |
|
и позволяет в некотором смысле характеризовать степень устойчивости разностной схемы.
Для доказательства второго утверждения теоремы возмутим правую часть уравнения (4.20); погрешность начальных данных теперь отсутствует. Выражение (4.22) для погрешности теперь выглядит следующим образом:
kqk f j .
k
106
