Boyarshinov_ChM_T2

Рис.2.2. Схема интегрирования обыкновенного дифференциального уравнения методом Рунге-Кутты с параметром = 1 .

Теперь рассмотрим схему6, получающуюся из выражения (2.11) при 1 2

(геометрическая интерпретация результата приведена на рис. 2.3):

h

yk 1 yk 2 f xk ,yk f xk h,yk hf xk ,yk .

1. Выполняется полный шаг метода Эйлера с целью определения приближенного значения искомой функции на конце отрезка интегрирования,

yk 1 yk h f xk ,yk .

2. Для этой же точки вычисляется приближенное значение производной

yk 1 f xk h,yk 1 .

3. Находится среднее значение двух производных, определенных на концах отрезка

1

yk 1/2 2 yk yk 1 .

4. Вычисляется значение искомой функции в конечной точке всего шага по схеме Эйлера с усредненным значением производной:

yk 1 yk h yk 1/2 .

Геометрически понятно, что получаемый указанным способом результат также должен быть “ближе” к истинному решению, чем получаемый по схеме Эйлера.

y

yk+1

yk 1

yk

6 Иногда получающееся выражение называют схемой (методом) Эйлера - Коши.

21

Рис.2.3. Схема интегрирования обыкновенного дифференциального уравнения методом Рунге-Кутта с параметром = 0,5

yk f xk ,yk yk ;

yk 1 yk h yk yk 1 h ;

yk 1 f xk h,yk 1 yk 1 h ;

Построим последовательность значений искомой функции:

Как и ранее, результаты получаемого численного решения для значения аргумента x=10 при различных шагах интегрирования приведены в табл. 2.2. Три верных значащих цифры получены теперь для шага h = 0,01.

22

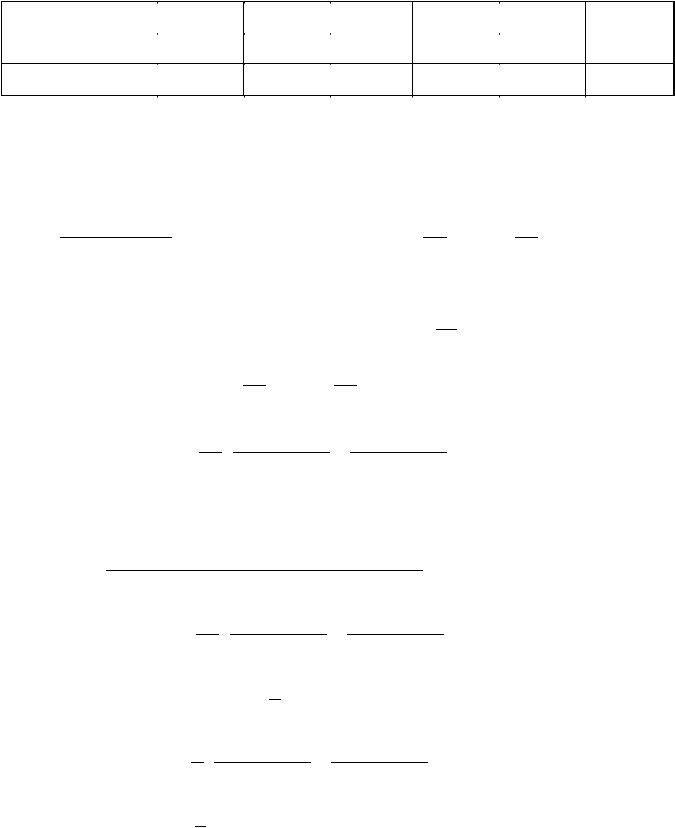
Таблица 2.2.

Результаты численного решения yn методом Рунге-Кутты второго порядка обыкновенного дифференциального уравнения y y с начальным условием y 0 1

Оценим погрешность аппроксимации уравнения (2.1) разностной схемой метода Рунге-Кутты. Как и ранее, подставляем точное решение в разностный

y xk f xk ,y xk h2 y xk fx xk ,y xk fy xk ,y xk f xk ,y xk O h2 .

23

Учитывая уравнение (2.1), а также выражение для производной

y xk y xk f xk ,y xk fx xk ,y xk fy xk ,y xk f xk ,y xk ,

окончательно получаем, что k O h2 , то есть метод Рунге-Кутты,

независимо от значения параметра , имеет второй порядок аппроксимации.

Методы Рунге-Кутты третьего и четвертого порядков аппроксимации

Рассмотрим две различные схемы Рунге-Кутты, предназначенные для численного решения обыкновенных дифференциальных уравнений первого порядка и имеющие третий порядок аппроксимации [5] :

Схемы Рунге-Кутты, имеющие четвертый порядок аппроксимации [5]:

Пример 2.5. Решим методом Рунге-Кутты четвертого порядка уравнение

В соответствии с приведенными выше соотношениями определяем коэффициенты

24

Построим последовательность значений искомой функции:

y0 y 0 1,

Результаты получаемого численного решения для значения аргумента x=10 при различных шагах интегрирования приведены в табл. 2.3. Три верных значащих цифры получены для шага h = 0,25.

Таблица 2.3.

Результаты численного решения yn методом Рунге-Кутты четвертого порядка обыкновенного дифференциального уравнения y y с начальным условием y 0 1

Сравнение таблиц 2.1 - 2.3 с решениями одной и той же задачи позволяет сделать вывод, что более высокая степень аппроксимации дифференциального уравнения разностным аналогом позволяет получать более точное решение при

25

более крупном шаге и, следовательно, меньшем числе шагов, то есть приводит к снижению требуемых ресурсов ЭВМ.

полиномом Ньютона: f x, y x F x

(2.12)

F xk 3 F xk 3,xk 2 x xk 3 F xk 3,xk 2,xk 1 x xk 3 x xk 2

F xk 3,xk 2,xk 1,xk x xk 3 x xk 2 x xk .

Здесь:

F xk 3,xk 2 F xk 3 F xk 2 ,

xk 3 xk 2

F xk 3,xk 2,xk 1 F xk 3,xk 2 F xk 2,xk 1 ,

xk 3 xk 1

F xk 3,xk 2,xk 1,xk F xk 3,xk 2,xk 1 F xk 2,xk 1,xk

xk 3 xk

- разделенные разности, являющиеся разностными аналогами соответствующих производных функции F(x).

Разделяем переменные в уравнении (2.1) и интегрируем его на отрезке xk , xk 1 :

xk 1

y xk 1 y xk f t,y t dt.

xk

Используя аппроксимацию (2.12), построим схему численного интегрирования дифференциального уравнения на отрезке xk , xk 1 :

26

xk 1 xk 1 xk 1

yk 1 yk F xk 3 dt F xk 3,xk 2 t xk 3 dt F xk 3,xk 2,xk 1 t xk 3 t xk 2 dt

xk xk xk

xk 1

F xk 3,xk 2,xk 1,xk t xk 3 t xk 2 t xk dt.

xk

Полагая шаг интегрирования h постоянным для всей сеточной области n , предыдущее выражение можно преобразовать к виду:

определяются методами Эйлера, Рунге-Кутты или другими способами. Кроме того, при интегрировании с переменным шагом h выражение (2.13) становится достаточно громоздким.

Вместе с тем метод Адамса имеет преимущества, например, перед методом Рунге-Кутта. Действительно, для определения очередного значения искомой функции вычислять правую часть дифференциального уравнения приходится лишь один раз, тогда как в методе Рунге-Кутты четвертого порядка такие вычисления приходится выполнять четырежды. Очевидно, что при достаточно сложном выражении, стоящем в правой части дифференциального уравнения, выигрыш во времени проведения расчетов будет значительным.

В монографии [10], посвященной методам решения обыкновенных дифференциальных уравнений, дополнительно представлены схемы Адамса - Башфорта второго

порядков аппроксимации.

Неявные схемы интегрирования

Рассмотренные выше методы решения задачи Коши относятся к явным схемам интегрирования, поскольку приводят к решению одного линейного

27

уравнения относительно очередного искомого значения функции. Примером неявных схем являются разностные аналоги Адамса-Моултона дифференциального уравнения (2.1) второго

h

yk 1 yk 2 f xk,yk f xk 1,yk 1

и четвертого

h

yk 1 yk 24 9f xk 1,yk 1 19f xk,yk 5f xk 1,yk 1 f xk 2,yk 2

порядков, приведенные в книге [10].

Для построения простейшей неявной схемы запишем уравнение (2.1) в форме

xk 1

y xk 1 y xk f t,y t dt,

xk

причем интеграл в правой части этого выражения вычислим по формуле трапеций:

Полученное выражение можно рассматривать как нелинейное уравнение относительно искомой величины yk 1 :

Эта схема допускает интегрирование с переменным шагом, не требует специальных приемов для начала расчетов. Вместе с тем требует исследования вопрос о существовании и единственности решения.

В частности, для k=0 получаем

y1 1 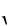1 h 2 h . h

Потребуем, чтобы дискриминант квадратного уравнения был неотрицательным:

28

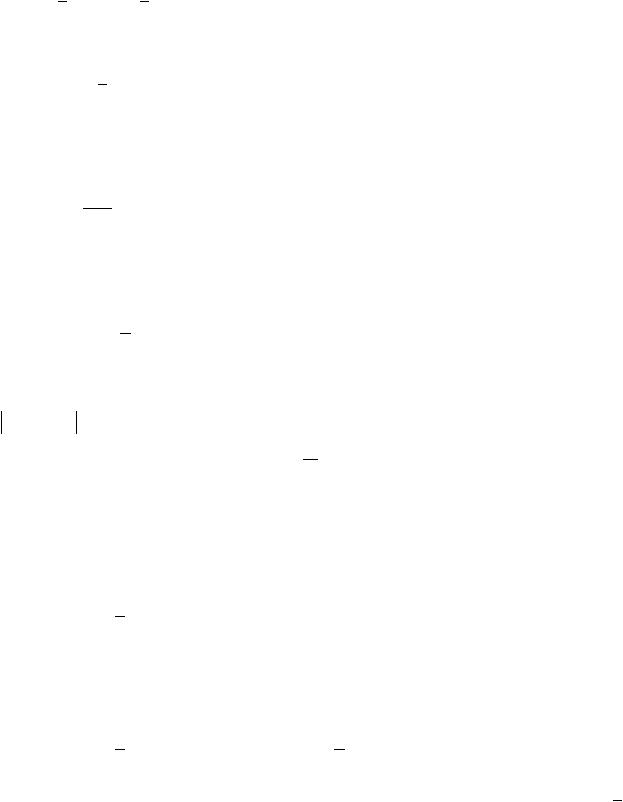
1 h 2 h 0,

h2 2h 1 0,

h 1 2 2,

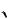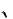2 1 h 2 1.

Принцип построение разностных схем требует, чтобы шаг интегрирования был положителен, то есть

0 h 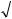2 1.

При иных значениях шага h численное решение будет содержать мнимую часть. В действительности точное решение исходного уравнения является вещественным:

y x 1 . 1 x

В общем случае решение нелинейного уравнения (2.14) можно находить с помощью итерационного процесса:

при малых шагах интегрирования h 2 , К - константа в условии Липшица для

K

правой части исходного дифференциального уравнения.

В то же время итерационный процесс (2.15) можно рассматривать следующим образом.

Пусть y(k0)1 yk . Тогда на первым шаге получаем решение

y(k1)1 yk h2 f xk ,yk f xk 1,yk yk h f xk ,yk ,

соответствующее использованию метода Эйлера, имеющего первый порядок аппроксимации.

Далее,

y(k2)1 yk h2 f xk ,yk f xk 1,y(k1)1 yk h2 f xk ,yk f xk 1,yk h f xk ,yk ,

что соответствует схеме Рунге-Кутта второго порядка с коэффициентом 1.

2

29

На третьей итерации можно ожидать повышения порядка аппроксимации до третьего, и так далее. Однако следует иметь в виду, что сама исходная схема (2.14) имеет второй порядок, а значит целесообразно ограничивать общее число итераций.

Известно эмпирическое правило [2]: пусть для решения дифференциального уравнения используется неявная схема p-го порядка точности, реализуемая итерационно. При первой итерации получается схема первого порядка точности; при второй - второго порядка, и так далее. При p итерациях получается схема p-го порядка. Дальнейшее увеличение числа итераций не повышает точности решения.

Дифференциальные уравнения высших порядков. Системы дифференциальных уравнений

Пусть имеется дифференциальное уравнение n-го порядка с n начальными условиями

Теперь уравнение (2.16) можно заменить системой дифференциальных уравнений первого порядка с соответствующими начальными условиями

Удобно систему уравнений и начальные условия представить в матричной форме:

d

dx u f , u 0 u0 . (2.18)

Здесь обозначено:

30