
Boyarshinov_ChM_T2
.pdf
|
0 |
0 j-1 |
j |
j+1 |
xРис. 5.10. Пятиточечный шаблон разностной схемы для уравнения |
||
|
эллиптического типа |
|
|
Оценим погрешность аппроксимации уравнения (5.45) разностным аналогом (5.49) с помощью разложения точного решения в ряды Тейлора:
u |
|
x |
j 1 |
,y |
k |
u |
|
x |
j |
,y |
k |
x |
|
x |
j |
,y |
k x |
x |
x |
j |
,y |
k |
h2 |
x |
j |
,y |
k |
h3 |
x |
x |
j |
,y |
k |
h4 |
|
x |
|
, |
|||||||
2 |
6 |
24 |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
u |
|
|
|
h |
|
u |
|
|
x |
u x |
|
|
x |
uiv |
|
|
|
x |
O h |
5 |
|
|||||||||||||||||
u |
|
x |
j 1 |
,y |
k |
u |
|
x |
j |
,y |
k |
x |
|
x |
j |
,y |
k x |
x |
|
j |
,y |
k |
h2 |
x |
j |
,y |
k |
h3 |
x |
|
x |
j |
,y |
k |
h4 |
|
x |
|
, |
||||||
|
2 |
6 |
24 |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
u |
|
|
|
h |
|
u x |
|
|
x |
u x |
|
|
x |
uiv |
|
|
|
x |
O h5 |
|
||||||||||||||||||
u |
|
x |
j |
,y |
k 1 |
|
|
j |
,y |
k |
y |
|
x |
j |
,y |
k |
y |
y |
x |
j |
,y |
k |
hy2 |
y |
j |
,y |
k |
hy3 |
u |
iv |
|
x |
j |
,y |
k |
hy4 |
|
h |
5 |
|
, |
||||
|
2 |
6 |
y |
24 |
y |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
u x |
|
|
u |
|
|
|
h |
|
u |
|
|
|
u x |
|
|
|
|
|
|
|
|
O |
|
|
|||||||||||||||||
u |
|
x |
j |
,y |
k 1 |
|
|
j |
,y |
k |
y |
|
x |
j |
,y |
k |
h |
y |
y |
x |
j |
,y |
k |
hy2 |
y |
j |
,y |
k |
hy3 |
u |
iv |
|
x |
j |
,y |
k |
hy4 |
|
|
5 |
|
. |
|||
|
2 |
6 |
y |
24 |
|
y |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
u x |
|
|
u |
|
|
|
|
u |
|
|
|
u x |
|
|
|
|
|
|
|
|
O h |
|
|||||||||||||||||||
Подставим эти выражения в формулу (5.49) вместо узловых значений и с учетом вида исходного дифференциального уравнения (5.45) получим:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
iv |
|
|
|
|
hx2 |
iv |
|
|
|
|
hy2 |
|
3 |
|
3 |
|
|||
|
jk |
|
x |
j |
,y |
k |
y |
j |
,y |
k |
|
W |
|
x |
j |
,y |
k |
|
|
u |
x |
x |
j |
,y |
k |
u |
y |
x |
j |
,y |
k |
|
|
x |
h |
y |
|
|
||
|
|
u x |
|
|
u x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
O h |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
uxiv xj ,yk |
h2 |
|
|
|
|
|
hy2 |
|
|
|
|
|
|
|
O hx2 hy2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
x uyiv xj ,yk |
|
O hx3 hy3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
12 |
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Это означает, что погрешность аппроксимации уравнения (5.45) разностной схемой (5.49) имеет второй порядок относительно шагов интегрирования.
Граничные условия первого рода (5.46) аппроксимируются точно. Для аппроксимации граничных условий второго рода и третьего рода рассмотрим схему на рис. 5.11.
|
|
Граница |
y |
|
n - нормаль |
¶G |
g |
||
k |
|
|||
k-1 |
|
|||
|
|
|
|
|
 j-1
j-1  j xРис. 5.11. Шаблон для аппроксимации граничных условий
j xРис. 5.11. Шаблон для аппроксимации граничных условий второго и тетьего рода
второго и тетьего рода
149

Граничное условие (5.47) аппроксимируется разностным выражением
ujk uj 1k |
cos |
ujk |
ujk 1 sin |
qjk , |
(5.50) |
hx |
|
|
hy |
|
|
граничное условие (5.48) - соответствующим ему разностным аналогом
ujk uj 1k |
cos ujk |
ujk 1 sin ujk |
Ujk . |
(5.51) |
hx |
|
hy |
|
|
Решение системы алгебраических уравнений (5.49) совместно с граничными условиями (5.46) (либо разностными аналогами (5.50), (5.51)
граничных условий второго и третьего родов) требует значительных ресурсов ЭВМ. Это приводит к необходимости использования итерационных методов для повышения точности численного решения.
В качестве альтернативы решение исходной задачи может быть найдено как стационарное решение некоторой эволюционной задачи. Например, вместо задачи (5.45) - (5.48) может рассматриваться нестационарное параболическое уравнение
u |
2u |
2u |
W x,y , |
x,y G |
t |
x2 |
y2 |
|
|
с произвольным начальным условием
u 0,x,y U x,y , |
x,y G |
и стационарными граничными условиями
u t,x,y U x,y , |
x,y GU , |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
u t,x,y |
|
x,y Gq |
, |
|
|
|
q x,y , |
|
|||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u t,x,y |
|
|
|
x,y G . |
|
|
u t,x,y U x,y , |
||||
|
n |
|
|
|
|
(5.52)
(5.53)
(5.54)
150

Для поиска стационарного решения задачи (5.52) - (5.54) могут быть использованы явные и неявные схемы, методы расщепления и факторизации:
- неявная схема
ujk ujk |
|
uj 1k 2ujk |
uj 1k |
|
ujk 1 2ujk ujk 1 |
|
~ |
|
|||||
|
|
|
h2 |
|
|
|
|
h2 |
|
Wjk ; |
|
||
|
|
|
|
x |
|
|
|
|
y |
|
|
|
|
- схема переменных направлений |
|
|
|
|
|||||||||
~ |
ujk |
~ |
~ |
|
~ |
|
ujk 1 2ujk |
ujk 1 |
Wjk |
|
|||
ujk |
uj 1k |
2ujk |
uj 1k |
; |
|||||||||
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
~ |
2hx |
~ |
|
|
2hy |
|
|
2 |
|
||
|
~ |
|
~ |
|
|
ujk 1 2ujk |
ujk 1 Wjk ; |
||||||
ujk |
ujk |
uj 1k |
2ujk |
uj 1k |
|||||||||
|
|
|
|
|
2 |
|
|
|
2 |
|
|
2 |
|
|
|
2hx |
|
|
|
2hy |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||
- явная схема |
|
|
|
|
|
|
|
|
|
|
|||
ujk ujk |
|
uj 1k 2ujk |
uj 1k |
|
ujk 1 |
2ujk ujk 1 |
Wjk . |
|
|||||
t |
|
|
2 |
|
|
|
2 |
|
|
||||
|
|
hx |
|
|
|
|
hy |
|
|
|
|
||
(5.55)
(5.56)
(5.57)
Рассмотрим последнюю схему более подробно. Полагая для упрощения hx hy h, из выражения (5.57) определим узловое значение
ujk |
ujk |
2 uj 1k |
uj 1k |
ujk 1 ujk 1 4ujk |
h2Wjk . |
(5.58) |
|
|
h |
|
|
|
|
Полученная схема условно устойчива при выполнении условия
h2 .
4
Для быстрейшего достижения стационарного решения следует выбрать шаг интегрирования по фиктивному времени наибольшим, то есть
h2 .
4
В этом случае выражение (5.58) после приведения подобных слагаемых принимает форму метода Ричардсона
ujk |
1 |
uj 1k |
uj 1k ujk 1 ujk 1 h2Wjk . |
|
4 |
|
|
В |
частном |
случае Wjk 0 (уравнение Пуассона) каждая определяемая |
|
величина |
ujk |
оказывается равной среднему значению четырех соседних |
|
узловых значений, |
|||
ujk |
1 |
uj 1k |
uj 1k ujk 1 ujk 1 . |
|
4 |
|
|
Ту же самую расчетную формулу метода Ричардсона можно получить из разностной аппроксимации (5.49) исходного уравнения, строя на ее основе итерационную вычислительную процедуру
151

ujn1k 2ujkn 1 |
ujn1k |
|
ujkn |
1 2ujkn 1 |
ujkn |
1 |
Wjk |
0, |
||
h |
2 |
|
|
h |
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
||
ujkn 1 41 ujn1k ujn1k ujkn 1 ujkn 1 h2Wjk .
Итерационный процесс по полученным формулам ведут до тех пор, пока для двух “соседних” итераций (n) и (n+1) выполняется условие
 u n 1 u n
u n 1 u n 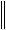 ,
,
где > 0 - малое число, а в качестве меры близости двух решений может быть взята, например, чебышевская норма
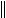
 max
max jk
jk  .
.
j,k
Процедура метода Ричардсона предполагает размещение в оперативной памяти компьютера одновременно двух массивов для хранения значений ujkn и ujkn 1 . Для экономии вычислительных ресурсов предпочтительнее использование итерационной схемы Либмана, получаемой на той же разностной схеме (5.49):
ujn11k |
2ujkn 1 |
ujn1k |
|
ujkn 11 2ujkn 1 |
ujkn |
1 |
Wjk |
0, |
||||||
|
|
h |
2 |
|
|
|
h |
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ujkn 1 |
|
41 ujn11k |
ujn1k |
ujkn 11 |
ujkn |
1 |
h2Wjk . |
(5.59) |
||||||
Расчеты в этом случае выполняются следующим образом (рис. 5.12).
y
u12n
|
|
u01n 1 |
u21n |
|
|
|
|
|
|
u |
n 1 |
|
|
|
|
10 |
|
xРис. 5.12. Реализация итерационной процедуры Либмана |
|
||||
Пусть величины |
u n 1 и |
u n 1 известны из граничных условий (5.46), а |
|||
значения u n и |
u n |
01 |
|
10 |
|
определены на предыдущей итерации. Тогда согласно |
|||||
12 |
21 |
|
|
|
|
выражению (5.59) можно определить величину |
|
||||
u11n 1 41 u01n 1 |
u21n |
u10n 1 u12n |
h2W11 . |
|
|
Затем можно вычислить |
|
|
|
||
152
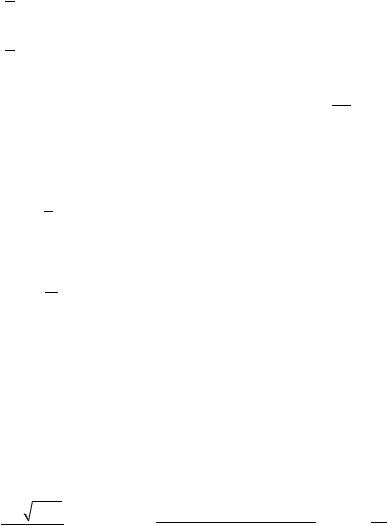
u21n 1 |
41 u11n 1 |
u31n |
u20n 1 |
u22n |
h2W21 , |
|
|
u31n 1 |
41 u21n 1 |
u41n |
u30n 1 |
u32n |
h2W21 , |
|
|
и так далее, производя вычисления всех искомых величин вдоль оси Ox при |
k |
||||||
=1. Аналогично |
определяются все ujn2 1 , |
j 0,n второго, третьего |
и |
||||
последующих слоев, пока не будут определены все искомые узловые величины.
Тождественно преобразуем выражение (5.59)
ujkn 1
и введем
ujkn 1
ujkn 1
ujkn |
1 ujn1k1 ujn1k ujkn 11 |
ujkn |
1 h2Wjk 4ujkn |
|||||
|
4 |
|
|
|
|
|
|
|
релаксационный параметр : |
|
|
|
|||||
|
|
|
|
|
|
|
h2Wjk 4ujkn , |
|
ujkn |
4 u |
jn1k1 |
ujn1k ujkn 11 ujkn |
1 |
||||
1 ujkn |
|
ujn1k1 ujn1k |
ujkn 11 |
ujkn |
1 h2Wjk . |
|||
4 |
||||||||
Полученное выражение представляет собой метод последовательной верхней релаксации. Метод сходится при условии 1 2. Оптимальное
значение релаксационного параметра с точки зрения быстроты достижения стационарного решения исходной задачи, согласно [13], для прямоугольной
области размером hxn hys определяется выражением |
|
|||||||||||
|
1 1 |
|
|
|
|
2 |
|
|
|
hx |
||
|
|
cos p / n |
|
|
|
|
cos p / s |
|
|
|
||
0 |
2 |
, где |
|
|
|
|
, |
. |
||||
|
1 |
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
h |
y |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
Контрольные вопросы и задания
Проверьте устойчивость разностного уравнения (5.49) по отношению к возмущениям правой части.
Покажите, что разностный аналог (5.50) граничного условия (5.47) имеет первый порядок аппроксимации. Предложите схему аппроксимации второго порядка для этого граничного условия.
Покажите, что разностный аналог (5.51) граничного условия (5.48) имеет первый порядок аппроксимации. Предложите схему аппроксимации второго порядка для этого граничного условия.
Проверьте условия устойчивости, порядок аппроксимации и оцените сходимость решения разностного уравнения (5.55).
Проверьте условия устойчивости, порядок аппроксимации и оцените сходимость решения разностного уравнения (5.56).
153
Проверьте условия устойчивости, порядок аппроксимации и оцените сходимость решения системы разностных уравнений (5.57).
Предложите свой способ расщепления (факторизации) эволюционного уравнения (5.52). Проверьте для него условия устойчивости, порядок аппроксимации и оцените сходимость к точному решению исходной задачи (5.45).
Разработайте способ реализации алгоритма Либмана (5.59) при заданных граничных условиях типа (5.47) или (5.48).
154
6 . П Р И К Л А Д Н Ы Е З А Д А Ч И
МА Т Е М А Т И Ч Е К О Г О
МО Р Д Е Л И Р О В А Н И Я
Аккумуляция лесным массивом и вторичный вынос загрязняющих веществ
Данные аналитических исследований состояния воздушной среды городов с высокой экологической нагрузкой при наличии больших лесных массивов свидетельствуют о сложных процессах накопления и трансформации загрязняющих веществ в приземном слое атмосферы этих агломераций. В результате проведения натурных замеров загрязнения воздушной среды одного из районов города Перми на территории, прилегающей к лесопарковому комплексу, а также непосредственно в самом лесном массиве, выявлена определенная аккумулирующая способность этих массивов. Накопление загрязняющих веществ наблюдается в случае повышенной концентрации примесей в атмосферном воздухе при направлении ветра “от источника загрязнения”. При смене ветра или его прекращении происходит постепенное “вымывание“ загрязняющих веществ, в ряде случаев - по направлению “к источнику загрязнения”. При некоторых условиях отмечается аномальное повышение концентрации веществ в воздушной среде и при временно неработающем источнике загрязнения.
Физическое объяснение ситуации может выглядеть следующим образом. Основная масса воздушного потока обтекает препятствие в виде лесного массива, при этом внутрь леса попадает незначительная часть этого потока, чем, в свою очередь, обусловлено снижение скорости здесь в 10 и более раз [15]. Это означает, что частицы примеси, заносимые ветром вглубь леса, начинают дрейфовать со значительно меньшей скоростью, нежели в основном потоке. В результате этого лес начинает играть роль накопителя загрязняющей примеси, сохраняющего ее даже в том случае, когда первичный источник прекращает действовать, и внешний “чистый” поток воздуха уносит все загрязнение из окружающей области. Очевидно, что смена направления ветра приводит к выносу ранее накопленных частиц примеси из леса, играющего теперь роль вторичного источника загрязнения. Понятно, что в рамках этой модели основной причиной накопления и вторичного выброса загрязняющих веществ является резкое замедление скорости воздушного потока внутри лесного массива.
Необходимо отметить, что предполагаемый механизм может быть не единственным и зависеть, например, от степени поглощения и последующего выделения растительностью рассеянных в воздушном потоке веществ. В рамках такой частной "механистической" постановки нет возможности учесть влияние
155

осадков (дождя и снега), влажности воздуха, температурной неравномерности, взаимодействия примесей между собой с образованием новых соединений и ряда других факторов.
Рис. 6.1. Схема расчетной области
Для количественного анализа возможности накопления вредных веществ в лесном массиве в соответствии с представленной выше физической моделью целесообразно в первом приближении [16] рассмотреть простейшее дифференциальное уравнение, описывающее процесс переноса и рассеивания примеси одномерным воздушным потоком, имеющим переменную скорость
|
V(x) |
|
|
2 |
t |
x |
x2 |
сначальным
(0,x) L (x)
и граничными условиями (рис. 6.1)
(t,0) L(t ), |
t,L |
0 |
|
x |
|
В уравнениях (6.1) - (6.3) обозначено:
(6.1)
(6.2)
(6.3)
- концентрация примеси;
- коэффициент диффузии;
t- время;
L - концентрация примеси на границе (фоновая концентрация);
L - граница исследуемой области;
L - длина рассматриваемого участка; предполагается, что лесной массив занимает 1/3 часть всего рассматриваемого отрезка;
V(x) - продольная скорость движения воздушного потока; предполагается, что внутри леса скорость движения воздуха составляет 10% от величины скорости ветра перед и после лесного массива; это соответствует тому, что большая часть воздушного потока (90%) обтекает лесной массив с внешней стороны.
156

На входной границе концентрации определяются источниками, находящимися за пределами рассматриваемой области, и назначаются из экспериментальных данных. Например, для суммы углеводородов концентрация на участке вблизи лесного массива составляет около 1,2 мг / м3. На выходной границе L, удаленной от возмущающего поток препятствия,
можно считать поток примесей установившимся, то есть 0.
x
Рассмотрим ряд неявных разностных схем
j |
j |
|
j 1 j 1 |
|
|
|
|
|
|
|
|||
|
|
Vj |
|
2h |
|
h2 |
j 1 2 j |
j 1 |
(6.4) |
||||
j |
j |
|
j 1 j |
|
|
|
|
|
|
|
|
|
|
|
|
Vj |
|
h |
h2 |
j 1 |
2 j |
j 1 |
(6.5) |
||||
j |
j |
|
j |
j 1 |
|
|
|
|
|
|
|
|
|
|
|
Vj |
|
h |
h2 |
j 1 |
2 j |
j 1 |
(6.6) |
||||
для приближения уравнения (6.1), различающихся способом аппроксимации частной производной по координате. Нетрудно убедиться, что погрешность аппроксимации исходного уравнения (6.1) каждой из приведенных схем имеет первый порядок относительно t. Схема (6.4) имеет второй порядок, а схемы (6.5) и (6.6) - первый порядок аппроксимации относительно шага интегрирования h. Разностная схема (6.4) устойчива при выполнении условия
h 2 , V 0, V
независимо от величины шага . При V = 0 получаем неявную безусловно устойчивую разностную схему (4.18). При V > 0 разностная схема (6.5) устойчива при выполнении условия
h . |
(6.7) |
V |
|
Разностная схема (6.6) безусловно устойчива при V > 0. При смене направления движения, то есть V < 0 , становится безусловно устойчивой схема (6.5), а схема (6.6) устойчива при выполнении условия (6.7).
Поскольку в поставленной задаче речь идет о смене направления воздушного потока в течение времени наблюдения, целесообразно воспользоваться разностной схемой (6.4), свойства устойчивости которой не зависят от направления ветра.
Использование этой разностной схемы для всех внутренних узлов приводит к системе алгебраических уравнений вида
|
2 h |
2 |
|
|
2 |
j |
, |
j 2,N 1 |
(6.8) |
Vjh 2 j 1 |
|
2 j |
Vjh 2 j 1 |
2h |
N - число узлов по длине участка L.
157

Для замыкания этой системы алгебраических уравнений используются граничные условия (6.3):
1 |
(t,0) L(t ), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
h |
2 |
|
|
|
h |
2 |
|
|
|
|
|
|
|
|
|
N |
|
h |
|
N |
|
|
N |
|
N |
VN |
N |
|
|||||||||||
N 1 |
N |
|
|
|
x2 |
|
|
N |
x |
h |
|
|
t |
x |
|
||||||||||
|
|
|
|
x |
|
|
|
2 |
|
|
2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
2 |
|
|
h |
2 |
|
|
N |
|
|
|
|
|
|
|
|
|
||
|
N |
VN h |
h |
|
|
|
N |
. |
|
|
|
|
|
|
|
|
|||||||||
N |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
x |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
С |
учетом |
|
граничного |
|
условия |
|
|
|
0 |
последнее алгебраическое |
|||||||||||||||
|
|
x x L |
|||||||||||||||||||||||
уравнение принимает вид: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
h2 |
|
|
|
|
|
h2 |
|
N . |
|
|
|
|
|
|
|
|
|
|
(6.9) |
||
N 1 |
1 |
|
|
N |
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Для начала расчетов поле концентраций предполагалось известным и равным
i |
(0,xi ) L (xi ), |
i 1,N . |
Расчеты режимов проводились для следующей схемы. Длина всей области составляет L = 10000 метров; из них на лесной участок, расположенный посередине, отводится 3500 метров. Скорость ветра на открытом участке равна 10 м/с, внутри леса - не превышает 1 м/с. Рассматривается процесс переноса примесей, осуществляемый по следующему режиму:
0 ... 1000 с - вдув в рассматриваемую область примеси с заданной концентрацией 1,2 мг/м3 (рис. 6.2).
1000 ... 2000 с - снижение концентрации примесей на входе в область до нулевого значения, что соответствует прекращению работы источника примеси (рис. 6.3).
2000 ... 3000 с |
- |
отсутствие ветра, то есть период |
свободного |
"растекания" примесей за счет процессов рассеивания (рис. 6.4). |
|
||
3000 ... |
- |
вдув с противоположной стороны |
относительно |
"чистого" воздушного потока (рис. 6.5). Приведенные результаты расчетов позволяют детально проследить динамику изменения концентрации примесей в районе, граничащем с лесным массивом.
158
