
Boyarshinov_ChM_T2
.pdf
Запишем это выражение в виде
maxqmax f j kqk
kmax
иоценим модуль этого выражения
max |
|
f j |
|
k |
|
qmax |
qk . |
||||
|
|
|
|
k max |
|
Как и в предыдущем случае, выберем узел, в котором q достигает наибольшего значения. Одновременно усилим последнее неравенство, учитывая определение чебышевской нормы и заменяя в правой части все величины  qk
qk 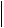 на
на 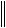 q
q , а
, а 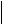 f j
f j - на
- на 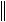 f
f :
:
max |
|
f |
|
q |
q k . |
||
|
|
|
k max |
Преобразуем полученное выражение к виду
|
max |
|
|
|
|
f , |
|
k |
q |
||||
|
|
|
k max |
|
|
|
откуда с учетом (4.24) получаем
|
|
|
|
max |
|
|
|
f , |
|
|
q |
|
k |
q |
|||||
|
|
|
|
|
k max |
|
|
|
|
|
|
|
f |
f , |
|
1 |
, |
||
q |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
что совпадает с определением устойчивости разностной схемы по правой части. Что и требовалось доказать.
Необходимо подчеркнуть, что условия теоремы формулируют лишь достаточные условия устойчивости. Иначе говоря, невыполнение условий (4.23), (4.24) не означает неустойчивости разностной схемы.
Пример 4.2. Проверим условия устойчивости для неявной разностной схемы (4.18) задачи теплопроводности
|
|
|
|
|
1 |
2 |
|
|
|
|
1 |
||||||
q j 1 |
|
h |
2 |
|
q j |
|
2 |
|
q j 1 |
|
h |
2 |
|
q j . |
|||
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
||
Коэффициенты уравнения равны:
max |
1 22 , |
j 1 |
2 , |
j 1 |
2 , |
j |
1 . |
|
h |
|
h |
|
h |
|
|
Условие устойчивости по начальным данным (4.23) принимает вид неравенства
1 2 |
|
|
1 |
, |
h2 |
h2 |
h2 |
|
|
107
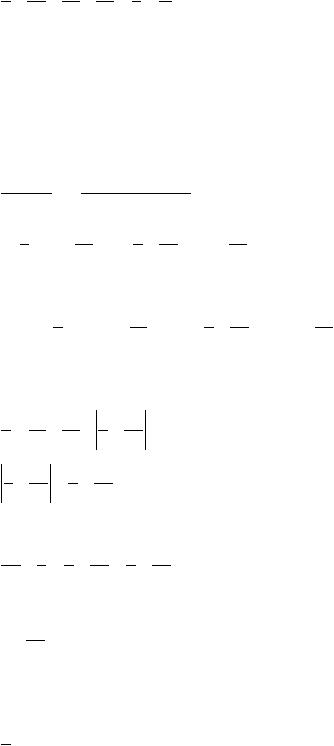
выполняющегося для любых значений шагов и h. Следовательно, рассмотренная разностная схема безусловно устойчива.
Условие устойчивости по правой части
1 2 |
|
|
1 |
|
h2 |
h2 |
h2 |
|
|
также выполняется для всех значений шагов и h (например, для 0 < < 1).
Общий вывод: рассмотренная неявная разностная схема безусловно устойчива как по начальным данным, так и по правой части.
Пример 4.3. Проанализируем (для сравнения) явную разностную схему (4.16) для той же задачи:
q j |
q j q j 1 2q j |
q j 1 , |
|
|
|||||||
|
|
|
|
|
h2 |
|
|
|
|
|
|
|
1 |
q j 1 |
|
1 |
|
2 |
q j 1 |
|
|||
q j |
|
h |
2 |
q j |
h |
2 |
h |
2 . |
|||
|
|
|
|
|
|
|
|
||||
Очевидно, что в этом случае отличны от нуля коэффициенты
max |
1 , |
j 1 |
|
, |
j |
|
1 2 |
, |
j 1 |
. |
|
|
|
h2 |
|
|
|
h2 |
|
|
h2 |
Условие устойчивости по начальным данным (4.23) принимает вид неравенства
1 |
|
|
|
|
1 |
2 |
, |
|||
|
h |
2 |
|
h |
2 |
|
|
h |
2 |
|
|
|
|
|
|
|
|
|
|||
12 1 2 ,
h2 h2
раскрывая которое
2 1 1 2 1 2 h2 h2 h2
получаем условие устойчивости по начальным данным:
|
h2 |
(4.26) |
. |
||
|
2 |
|
Это означает, что рассматриваемая схема является условно устойчивой. Условие устойчивости по правой части
выполняется для всех значений 0 < < 1.
108

Общий вывод: явная разностная схема является условно устойчивой при выполнении условия (4.26), ограничивающего величину шага интегрирования
.
Оценка устойчивости разностных схем методом Неймана20
Вновь рассмотрим разностную схему (4.16)
|
q j 1 2q j q j 1 . |
|
q j q j |
|
|
|
h2 |
|
Если внести возмущение q в решение q |
на каком-либо временном слое, |
|
~ |
решение на следующем слое |
q~ q q будет удовлетворять |
q q q , |
||
уравнению
~ |
~ |
|
q j |
q j |
|
|
|
|
~ |
~ |
~ |
q j 1 |
2q j |
q j 1 . |
|
h2 |
|
Вычитая из этого выражения предыдущее, получим уравнение относительно погрешностей
|
q j q j 1 |
2q j |
q j 1 , |
|
|
||||
q j |
|
|
|||||||
|
|
|
|
|
|
h2 |
|
|
|
которое удобно переписать в виде |
|
|
|||||||
|
q j 1 |
|
|
|
2 |
|
|||
q j |
h |
2 q j 1 |
2 q j 1 |
h |
2 . |
||||
|
|
|
|
|
h |
|
|
||
Разложим погрешность q решения в ряд |
|||||||||
|
N 1 |
|
|
|
|
|
|
|
|
q x akeikx |
, |
|
|
|
|
(4.27) |
|||
|
k 0 |
|
|
|
|
|
|
|
|
где eikx , |
k 0,N 1 |
- |
полная ортогональная система функций на равномерной |
||||||
сетке N xk |
xk k h, |
k 0,N . |
|
|
|||||
Здесь i 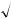 1 - мнимая единица.
1 - мнимая единица.
Подставим k-ю гармонику k x akeikx этого разложения в уравнение:
q jk h2 akeikxj 1 1 2h2 ak eikxj h2 ak eikxj 1
ake |
ikxj |
|
|
e |
ikh |
2 e |
ikh |
|
kake |
ikxj |
k |
, |
|
|
1 |
|
2 |
|
|
|
|
kq j |
|||||
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 Джон фон Нейман [28.12.1903 - 8.2.1957] - американский математик. В 1926 году окончил Будапештский университет. В 1927 - 1929 годах преподавал в Берлинском университете, 1930 - 1933 - в Принстонском университете. С 1933 года - профессор Принстонского института перспективных исследований. С 1940 года - консультант армейских и морских учреждений; принимал участие в работах по созданию первой атомной бомбы. С 1954 года - член комиссии по атомной энергии. Внес большой вклад в создание первых ЭВМ и разработку методов их применения.
109

где |
k |
|
|
|
|
- коэффициент роста k-ой гармоники при |
|
1 |
|
2 |
e ikh 2 eikh |
||||
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
переходе на следующий временной слой. Очевидно, что для m временных слоев получаем соотношение:
qmj k |
k m q0j k . |
(4.28) |
Учитывая известную формулу Эйлера, выражение для коэффициента роста произвольной гармоники можно преобразовать к виду
k 1 2 e ikh 2 eikh
h
1 |
2 |
cos kh i sin kh 2 cos kh i sin kh |
(4.29) |
||||||
|
|
h |
|
|
|
|
|
|
|
1 |
|
|
4 |
2 |
kh |
|
|||
h |
2 |
2cos kh 2 1 |
2 sin |
|
|
. |
|
||
|
|
|
h |
|
|
|
2 |
|
|
В более общем виде разностное уравнение |
|
||||||||
B uj |
uj Auj j |
|
|
|
|
(4.30) |
|||
|
|
|
|
|
|
|
|
|
|
относительно погрешностей |
uj |
|
(при отсутствии возмущения |
правой части) |
|||||
можно записать в виде:
B uj B A uj .
Подставляя сюда выражение (4.28) для uj , получаем уравнение для определения коэффициента роста произвольной гармоники:
k Beikxj |
B A eikxj . |
Теорема 4.4 (признак устойчивости Неймана). Разностная схема с постоянными коэффициентами устойчива по начальным данным, если для всех k выполняется неравенство
k |
1 C , |
C const 0. |
(4.31) |
Доказательство. Разложим погрешность начальных данных в ряд (4.27)
N 1
u t0 ,xj akeikxj .
k 0
Подстановка этого разложения в разностную схему (4.30) благодаря ее линейности приводит к выражению
N 1
u tm ,xj k m akeikxj . k 0
110

На сетке N в силу ортогональности гармоник21
u tm |
2 |
N 1 |
2 |
2m |
N maxk |
k |
2m N 1 |
2 |
|
|
l2 |
N ak |
k |
ak |
|
max k |
|||||
|
|
k 0 |
|
|
|
|
k 0 |
|
|
k |
2m |
u t0 |
2 |
|
. |
|
|
|
l2 |
Наконец, в соответствии с условием (4.31),
u tm l2 |
1 Ñ 2m |
u t0 l2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
u tm l |
1 Ñ m |
u t0 l . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Последнее выражение как раз и соответствует признаку равномерной |
||||||||||||||||
устойчивости. Что и требовалось доказать. |
|
|
|
|
|
|
|
|
|
|
||||||
Терема 4.5 (признак неустойчивости). Если хотя бы для одного |
k |
|||||||||||||||
коэффициент роста |
|
гармоники |
k |
|
|
нельзя |
|
|
мажорировать величиной |
|||||||
1 C , C const , то разностная схема (4.30) неустойчива. |
|
|
|
|
|
|||||||||||
Доказательство. Пусть в начальный момент имеется ошибка вида eikx |
|
для |
||||||||||||||
заданной гармоники |
k. Тогда к моменту |
|
t = mt |
она возрастет в k m |
раз, |
что |
||||||||||
по модулю |
больше |
|
величины |
1 C |
|
m |
1 C |
|
t |
Ct |
при сколь |
угодно |
||||
|
|
|
|
|
|
|
||||||||||
большом C. Но неограниченный рост ошибки как раз и означает |
||||||||||||||||
неустойчивость схемы. Что и требовалось доказать. |
|
|
|
|
|
|
|
|||||||||
Вновь вернемся к разностной схеме (4.16), для которой коэфициент роста |
||||||||||||||||
гармоник определяется выражением (4.29). В силу того, что функция |
sin |
2 |
kh |
|||||||||||||
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
может изменяться в пределах от 0 |
до 1, наименьшее значение коэффициента |
|||||||||||||||
роста гармоник равно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4k 1 h2
и может стать меньше -1. Ограничим его значение в соответствии с требованием теоремы 4.4:
k |
1 4 2 |
1. |
|
h |
|
Отсюда,
1 1 4 1, h2
4
h2 2,
21 Согласно [10], |
под l2 понимается эвклидово пространство |
-мерных векторов a a0 ,a1 , со скалярным |
||||
|
|
|
|
|
|
1 2 |
произведением |
a,b akbk |
и нормой a |
ak2 |
|
||
a,a |
. |
|||||
|
k 0 |
|
|
|
|
|
|
|
|
k 0 |
|
|
|
111

h2
2 ,
что соответствует полученному ранее с помощью принципа максимума условию устойчивости по начальным данным (пример 4.3).
Сходимость решения разностной схемы
Разностная схема (4.20) корректна, если ее решение существует и единственно при любых входных данных, а сама разностная схема является
устойчивой.
Разностное решение uh задачи (4.20) сходится к решению u задачи (4.19),
если
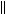 uh u
uh u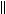 0.
0.
h 0
Теорема 4.6. Если решение u задачи (4.19) существует, разностная схема (4.20) корректна и аппроксимирует задачу (4.19) на данном решении, то разностное решение сходится к точному22.
Доказательство. |
Согласно |
введенному |
определению |
понятия |
||||||
аппроксимации |
|
|
|
|
|
|
||||
|
h |
A u f |
h |
, |
|
|
|
|
||
|
h |
|
|
|
|
|
|
|||
|
|
R u |
|
. |
|
|
|
|
||
|
h |
h |
|
|
|
|
||||
|
h |
|
|
|
|
|
|
|
||
Отсюда следует, что |
|
|
|
|||||||
A u f |
h |
|
h |
, |
|
|
|
|
||
|
h |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
. |
|
|
|
|
R u |
h |
h |
|
|
|
|
||||
|
h |
|
|
|
|
|
|
|
||
Но теперь решение u можно рассматривать как возмущенное по сравнению с uh решение задачи (4.20), соответствующее внесенным возмущенниям h правой части и h краевых условий.
В силу устойчивости разностной схемы имеет место утверждение:
0 |
0, |
uh u , |
как только |
h , |
h |
. |
||
С другой стороны, в силу свойств аппроксимации, |
|
|
||||||
0 |
h0 0, |
h |
, |
h |
при |
h h0. |
|
|
Теперь очевидно, что |
|
|
|
|
|
|
||
0 |
h , |
uh u |
|
при |
h h0 . |
|
|
|
Что и требовалось доказать. |
|
|
|
|
||||
22 |
“Сокращенная” форма теоремы: из аппроксимации и устойчивости следует сходимость разностного |
|
|
|
решения. |
112
Теперь понятен порядок проведения исследования разностных схем: при выполнении условий аппроксимации, устойчивости и разрешимости
разностной схемы (4.20) получаемое численное решение будет сходиться к точному решению поставленной краевой задачи (4.19).
Теорема 4.7. Если условия предыдущей теоремы выполнены, операторы Ah и Rh линейные, порядок аппроксимации равен p, то точность имеет порядок не ниже p.
Представим условие устойчивости в виде
u1 u2 M0 |
f1 f2 M1 1 |
2 . |
(4.32) |
||||||
Используя |
определение |
погрешности решения |
zh uh u, запишем |
||||||
выражения (4.20) в виде |
|
|
|||||||
A z |
h |
|
h |
, |
|
|
|
||
h |
|
|
|
|
|
|
|||
|
|
|
|
|
. |
|
|
|
|
R z |
h |
h |
|
|
|
|
|||
h |
|
|
|
|
|
|
|||
Применяя к полученным соотношениям формулу (4.32), получаем:
zh M0 h M1 h . |
|
|
|
В силу условия теоремы h |
0hp , |
h |
1hp , откуда |
 uh u
uh u Mhp , M 0 M0 1 M1 . Что и требовалось доказать.
Mhp , M 0 M0 1 M1 . Что и требовалось доказать.
Контрольные вопросы и задания
Запишите условия согласования начальных (4.3) и граничных (4.5) (или (4.6)) условий для задачи (4.2).
Запишите условия согласования начальных (4.11) и граничных (4.12) условий для задачи (4.10).
Покажите, как с помощью замены переменных задачу (4.2) - (4.4) можно свести к задаче с однородными граничными условиями (4.13).
Укажите условия, при которых решение задачи (4.13) можно представлять в форме (4.14).
Проверьте порядок аппроксимации граничного условия (4.5) разностным аналогом (4.21) относительно шагов интегрирования и h.
Следует ли из равномерной устойчивости разностной схемы, что она устойчива и в обычном смысле? Справедливо ли обратное утверждение?
Укажите смысл коэффициента C в уловии устойчивости (4.25). Оцените порядок аппроксимации граничного условия (4.5) неявным вариантом схемы (4.21).
113

5 . С Е Т О Ч Н Ы Е С Х Е М Ы Д Л Я У Р А В Н Е Н И Й В Ч А С Т Н Ы Х П Р О И З В О Д Н Ы Х
Уравнения первого порядка
Рассмотрим одномерное движение (например, в прямолинейной трубке) частицы, состояние которой определяется функцией u t,x t , то есть зависит от времени t и ее положения x(t). Скорость изменения состояния частицы (в эйлеровой системе отсчета) определяется полной производной по времени:
du u u dx u v u |
, |
|||
dt t |
x dt |
t |
x |
|
v - cкорость перемещения частицы, которую для упрощения будем считать постоянной в течение всего исследуемого периода [0, T].
Если скорость изменения состояния частицы f t,x t известна, то простейшее уравнение переноса (дифференциальное уравнение первого порядка) имеет вид
u |
v u f t,x t . |
(5.1) |
t |
x |
|
В качестве кревых условий примем, что |
|
|
|
|
|
u 0,x U x , |
(5.2) |
|
|
|
|
u t,0 U t .
0
Естественно потребовать выполнение условий сопряжения U 0 U0 0 . Фактически речь идет о смешанной задаче Коши, поскольку заданы начальные условия по обеим независимым переменным.
Схемы бегущего счета |
|
|
|
|
|
|
|
|
Расмотрим |
задачу |
(5.1) |
- (5.2) |
в |
области G 0 t T 0 x L , для |
|||
которой построим сетку |
|
|
|
|
|
|
|
|
|
ti i , |
i 0,m, |
T |
; |
xj |
j h, |
j 0,n, n |
L |
ti ,xj |
m |
. |
||||||
|
|
|
|
|
|
|
|
h |
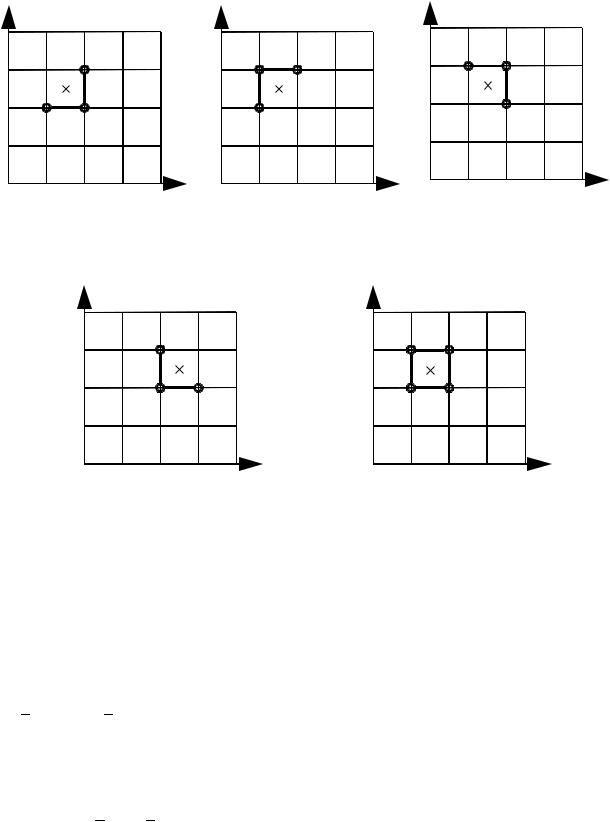
Рассмотрим разностную схему, аппроксимирующую дифференциальное уравнение (5.1) на простейшем шаблоне (рис. 5.1а):
t
117
i+1 i
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
j-1 |
j |
j+1 |
x |
0 |
j-1 |
j |
j+1 |
x |
0 |
j-1 j |
j+1 |
x |
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
б |
|
|
|
|
в |
t
i+1
i
0
0 |
j-1 |
j |
j+1 |
x |
0 |
j-1 |
j |
j+1 |
|
г |
|
|
|
|
д |
|
|
Рис. 5.1. Варианты шаблонов для аппроксимации уравнения переноса.
Разностное соотношение для дифференциального уравнения (5.1) записывается в виде:
1 |
uj |
uj |
v |
|
~ |
(5.3) |
|
|
h |
uj uj 1 f . |
|||||
|
|
|
|
|
|
||
Выражение, стоящее в правой части этого соотношения, вычисляется для |
|||||||
центра ячейки (на рис. 5.1а указано символом |
): |
||||||
~ |
|
|
|
h |
|
|
|
f |
|
f ti |
|
, xj |
. |
|
|
|
|
|
2 |
|
2 |
|
|
Проверим свойства разностной схемы (5.3). Для оценки порядка аппроксимации воспользуемся разложениями решения и правой части в ряды Тейлора:
118
