Boyarshinov_ChM_T2

а

б

в

г

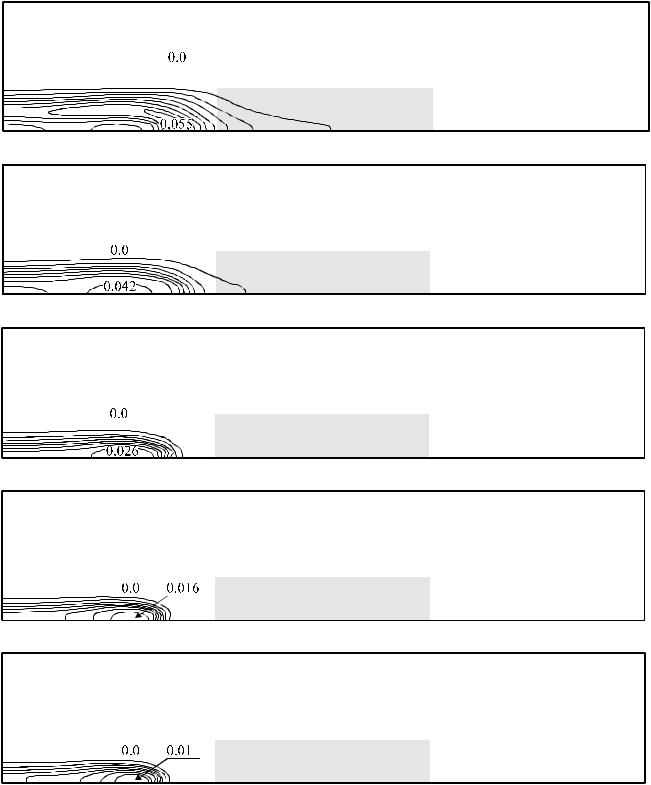
Рис. 6.11. Концентрации примеси в воздушном потоке при поступлении чистого воздуха с

противоположного направления. Время процесса 325 с (а), 350 с (б), 375 с (в) и 400 с (г).

177

а

б

в

г

д

Рис. 6.12. Концентрации примеси в воздушном потоке при поступлении чистого воздуха с противоположного направления.

Время процесса 450 с (а), 500 с (б), 600 с (в), 700 (г) и 800 с (д).

178

Движение потока жидкости по системе каналов городского коллектора

Одной из основных причин загрязнения водоемов являются сточные воды промышленных предприятий, транспортируемые по системам канализации на станции биологической очистки воды, а затем сбрасываемые в естественные водоемы. В связи с этим важнейшей проблемой становится регулирование сброса загрязняющих веществ через системы канализации на очистные сооружения и в водоемы - приемники сточных вод. Решение проблемы оптимального управления потоками требует построения математической модели движения жидкости с растворенными в ней примесями при заданных концентрациях примесей и расходах жидкости в точках сброса.

Как правило, системы канализации моделируются с использованием сетевых моделей на основе известных законов Кирхгофа. Это во многом ограничивает возможности моделей, поскольку заранее предполагает линейность происходящих процессов переноса жидкостей и растворенных в ней веществ. В предлагаемой работе принимаются следующие основные гипотезы:

-жидкость с растворенными в ней примесями считается идеальной и несжимаемой; концентрации примесей малы и не влияют на свойства жидкости

ихарактер течения; растворенные вещества в реакцию друг с другом не вступают, в осадок не выпадают и не испаряются с поверхности потока;

-скорости всех частиц жидкости в плоскости поперечного сечения одинаковы и направлены вдоль оси трубы, что позволяет перейти от многомерной задачи к одноосной модели движения; течение жидкости изменяется медленно, то есть характеристики потока являются достаточно гладкими функциями времени и координаты;

-форма трубы известна; ее стенки абсолютно жесткие и неподвижные; их влияние на течение учитывается с помощью коэффициентов шероховатости, характеризующих материал и состояние труб, физические свойства жидкости;

-при слиянии двух или более потоков (узлы канализационной системы) векторы скорости частиц жидкости поворчиваются мгновенно без изменения модулей; перемешивание потоков происходит мгновенно по всему сечению.

Канализационная система аппроксимируется набором прямолинейных участков труб, соединенных между собой. Это позволяет разделить задачу определения параметров потока и распределения концентраций на ряд связанных между собой подзадач для каждого участка в отдельности. При указанных допущения задача определения распределения скоростей и глубин потока, концентраций примесей для каждого прямолинейного участка сводится к интегрированию системы дифференциальных уравнений в частных производных [19]

- неразрывности

178

- сохранения массы (для каждого компонента раствора)

гидравлический радиус трубы. Показатель степени y(H) вычисляется согласно [19] по формуле Павловского:

y(H) 2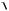5. nш 075. R(H)(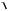nш 010. ) 013. .

179

Уравнения (6.26) - (6.28) содержат k+2 дифференциальных уравнений с k+2 неизвестными функциями V(t,s), H(t,s), Ci (t,s), i 12, ,...,k . В граничных условиях (6.29) - (6.31) предполагается, что жидкость втекает в трубу с левого края (s = 0) и вытекает из правого (s = L).

При построении связанного решения для разветвленной системы в целом учитывается, что скорости и глубины потоков жидкости на выходе каждого отдельного участка (с номером j) становятся граничными условиями на входе следующего участка трубы (с номером j+1):

Кроме того, при слиянии двух потоков ( с номерами p и q ) в один ( с номером r ) при вышеуказанных допущениях и использовании законов сохранения массы и количеcтва движения имеют место следующие соотношения:

представляющие собой нелинейные алгебраические уравнения относительно

Hr (t,0), Vr (t,0) при известных Hp (t,Lp ),Vp (t,Lp ) и Hq (t,Lq ),Vq (t,Lq ).

Дифференциальные уравнения (6.26) - (6.27) удобно представить в форме

где учтено, что площадь поперечного сечения потока жидкости в круглой трубе - известная функция глубины.

Для численного решения системы нелинейных неоднородных дифференциальных уравнений в частных производных (6.31) - (6.32) с граничными (6.29) - (6.30) и начальными (6.32) - (6.33) условиями используются конечно-разностные схемы следующего вида:

180

где h - шаг по координате, - шаг по времени; величины H и V относятся к “следующему" моменту времени (t+ ). Разностные схемы (6.43) и (6.44) являются неявными по построению, но могут быть разрешены явным образом. Для решения системы нелинейных алгебраических уравнений (6.35) - (6.40), (6.43) - (6.44) применяется метод Ньютона.

Дифференциальное уравнение (6.28) (индекс " l " опускается, поскольку для всех компонент раствора дальнейшие выражения принимают аналогичную форму) представим в виде:

Разностный аналог для него записывается в форме:

(6.46)

Cj (Hj ) (Hj ) Vj (Hj ) h (Hj 1 ) (Hj )Vj hVj 1 0

Алгоритм решения задачи (6.26) - (6.34) о переносе сточных вод по системе трубопроводов состоит из двух этапов [20]. На первом - решаются уравнения (6.43) - (6.44), позволяющие отыскать распределение глубин и скоростей потоков во всем коллекторе. Начальная скорость жидкости (при заданной глубине h потока) определяется из условия стационарности течения:

Далее, при известных параметрах потоков формируется и решается система уравнений (6.46), из которой определяются распределения концентраций всех примесей в узлах разностной сетки, то есть во всей канализационной системе.

При замене дифференциальных уравнений разностными аналогами чрезвычайно важным становится вопрос определения соотношения между шагами интегрирования по времени и координате, обеспечивающими устойчивость вычислительной схемы. В силу нелинейности исходной задачи аналитическое исследование свойств разностных схем затруднено. Поэтому проводилось компьютерное исследование вычислительной устойчивости на тестовом примере.

Длина трубы L=640 м, сечение - прямоугольник шириной 1,0 м, угол горизонтального наклона равен 1 градусу, коэффициент шероховатости nø =0,013 (старые бетонные трубы), уровень жидкости при первоначальном заполнении составляет H(s)=1,0 м. В течение 5 секунд (1/4 периода) на левом конце трубы высота потока возрастает по гармоническому закону с 1,0 м до 1,5 м, затем в течение следующих 5 секунд убывает до 1,0 м и фиксируется на этом

181

значении. Рассматриваемый режим соответствует формированию и распространению волны по поверхности жидкости.

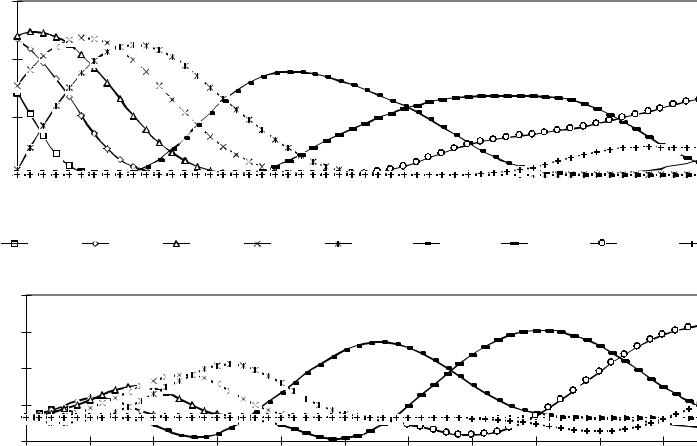
Результаты расчета представлены на рис. 6.13, где показаны графики изменения глубины и скорости потока жидкости вдоль оси трубопровода. На рис. 6.14 приведены результаты определения области устойчивости численного решения при различных соотношениях шагов интегрирования.

Вычисления показали, что используемая разностная схема в сочетании с методом Ньютона обладает хорошей устойчивостью лишь в малом диапазоне шагов по времени и координате (соответственно, t=0,05 ... 0,2 с и h= 0,25 ... 2,5 м). Это существенно ограничивает производительность модели при расчетах больших систем.

182