Boyarshinov_ChM_T2
.pdf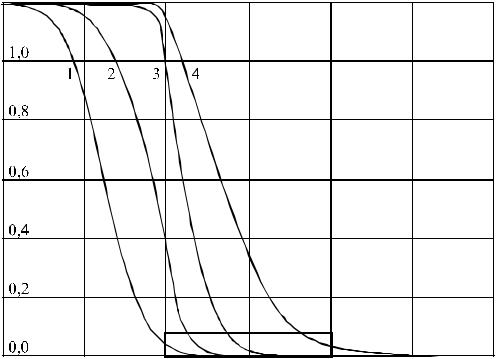
Рис. 6.2. Распределение концентрации примесей в области, содержащей лесной участок. Время процесса: 1 - 200 с; 2 - 300 с; 3 - 500 с; 4 - 1000 с.
В начальный период времени (от 0 до 350 секунд) поток воздуха свободно вносит в рассматриваемую область примесные вещества и достигает лесного участка. За счет процессов рассеивания граница переносимого потоком примесного компонента несколько размыта. В течение последующего времени (вплоть до момента времени 1000 секунд) происходит интенсивное насыщение леса примесными компонентами.
После окончания работы источника выбросов (начиная с момента 1000 секунд) насыщение области примесными веществами прекращается, и начинается перераспределение концентрации внутри рассматриваемой области. В этот период времени фактически происходят одновременно несколько процессов: перенос примесей с открытой площадки вглубь леса, небольшое диффузионное рассеивание внутри него, повышение концентрации за лесом и вынос примесей за пределы рассматриваемой зоны. К концу этого этапа перед лесным участком практически отсутствует концентрация примесных веществ, что объясняется устойчивым воздействием потока воздуха. Одновременно позади растительной зоны происходит значительное повышение концентрации примеси, преносимой ветром.
159
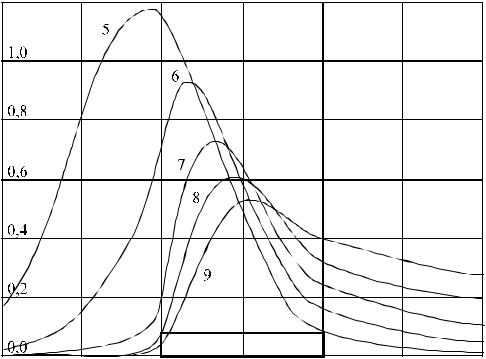
Рис. 6.3. Распределение концентрации примесей в области, содержащей лесной участок. Время процесса: 5 - 1200 с; 6 - 1400 с; 7 - 1600 с; 8 - 1800 с; 9 - 2000
с.
На очередном этапе рассматриваемого процесса (2000 - 3000 секунд) отсутствует ветер. В этот период преобладающее влияние оказывают процессы диффузионного распространения веществ, что приводит к "растеканию" концентрации примесей из лесного массива на открытую площадку перед ним, а также к выравниванию уровня концентрации позади леса.
На заключительном этапе (после 3000 секунд) определяющим фактором становится движение потока воздуха с "обратной" первоначальному направлению стороны. Это приводит к достаточно быстрому снижению концентрации в области за лесом и одновременно - к существенному повышению концентрации примесей перед лесным участком.
Вполне очевидно, что теперь накопленные в растительном покрове запасы примесных веществ становятся вторичным источником загрязнения даже при относительно чистом потоке воздуха, дующем со стороны, противоположной положению первичного источника загрязнения.
160
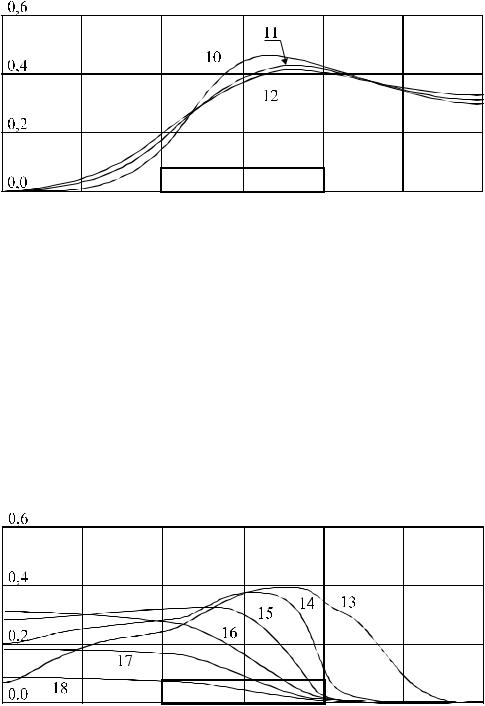
Рис. 6.4. Распределение концентрации примесей в области, содержащей лесной участок. Время процесса: 10 - 2400 с; 11 - 2800 с; 12 - 3000 с.
Понятно, что интенсивность такого вторичного загрязнения ниже, чем у оригинального источника, однако продолжительность воздействия может быть значительной в зависимости от размеров леса и времени накапливания примесных веществ при обдувании загрязненным потоком. Проведенное исследование позволяет заключить, что лесной массив при определенных метеорологических условиях действительно может становиться источником вторичного выброса примесей, характерных для производственного предприятия.
Рис. 6.5. Распределение концентрации примесей в области, содержащей лесной участок. Время процесса: 13 - 3200 с; 14 - 3400 с; 15 - 3800 с; 16 - 4600 с; 17 - 5500 с; 18 - 7000 с.
161
Для более точного описания процесса накопления лесным массивом и последующего выброса вредных примесей рассмотрим двухмерную (в
вертикальной плоскости) задачу о движении рассеянных примесных частиц в потоке воздуха, включающую дифференциальные уравнения
- Навье27 - Стокса28
u u u v u |
1 p |
|
|
2 |
u |
|
2 |
u |
|
Fx , |
||
|
|
|
|
|||||||||
t |
x |
y |
x |
x2 |
y2 |
|
|
|||||
(6.10)
v |
v |
v |
1 p |
2v |
2v |
Fy |
, x,y G, |
|||
u |
v |
|
y |
|
|
|
|
|
|
|
t |
x |
y |
x |
2 |
y |
2 |
|
|
||
- несжимаемости
u |
v 0, |
x,y G; |
|
|
|
|
|
|
|
|
|
|
|
||
x |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- диффузии |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
2 |
|
2 |
|
, |
|
|
|||||
u |
v |
|
2 |
|
y |
2 |
0, x,y G |
|
|
||||||
t |
x |
|
y |
x |
|
|
|
|
|
|
|
|
|||
с начальными |
|
|
|
|
|
|
|
|
|
|
|
|
|||
V(0, x) V |
(x ), |
(0,x) |
G |
(x), |
p(0,x) p |
G |
(x), |
x,y G |
|||||||
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
||
и граничными условиями
V(t,x) V G (t,x), |
(t,x) G(t,x), |
x,y G, |
n V 0, |
||||
|
|
|
|
|
|
|
|
V(t,x) 0, |
(t,x) 0, |
x,y G, |
n |
|
|||
V 0;. |
|||||||
n |
|
n |
|
|
|
|
|
(6.11)
(6.12)
(6.13)
(6.14)
(6.15)
Здесь дополнительно введены обозначения:
27Навье Анри [1785 - 1836] - французский инженер и ученый. Подготовил и опубликовал ряд трудов по строительной механике, сопротивлению материалов, теории упругости, гидравлике и гидромеханике.
28Стокс Джордж Габриель [13.8.1819 - 1.2.1903] - английский физик и математик. Окончил в 1841 году Кембриджский университет. С 1849 года становится профессором этого же университета. С 1851 года является членом Лондонского королевского общества, а с 1885 по 1890 год - его президент. Член Парижской академии наук.
162
V |
- вектор скорости движения воздуха с компонентами u и v; |
p |
- давление воздуха (гидростатическое давление исключается); |
F |
- вектор массовых сил; |
|
- коэффициент кинематической вязкости газовой смеси; |
|
- плотность газа; |
n |
- вектор нормали к границе области. |
Для записи конкретных граничных условий рассмотрим схему на рис. 6.6а.
Скорости. G1 - задано распределение скоростей |
u и |
v вдоль этой |
границы. Считается, что вертикальная составляющая |
v |
скорости здесь |
отсутствует, горизонтальная составляющая изменяется от нулевого значения в низшей точке до наибольшего значения в высшей точке по квадратичному закону.
G2 - вертикальная скорость v на достаточно большой высоте обращается в нуль; u сохраняет максимальное значение вдоль всей границы. Очевидно, что для определения "достаточной высоты" необходим численный эксперимент.
G3 - "выходная" граница области. При значительном удалении от лесного массива воздушный поток "установится", что будет соответствовать граничным условиям
u 0, |
v 0. |
|
x |
x |
|
G4 - |
приземный слой. Считается, что вблизи поверхности скорость |
|
воздушной |
смеси равна 0, то есть u 0, |
v 0, что соответствует полному |
"торможению" газового потока.
Концентрации. G1 - на входной границе концентрации определяются источниками, находящимися за пределами рассматриваемой области, и
назначаются из экспериментальных данных.
163
G2 - для достаточно большой высоты можно полагать y 0.
G3 - на выходной границе, удаленной от возмущающего поток
препятствия, можно считать поток примесей установившимся, то есть |
0. |
|
|
|
x |
G4 - на поверхности почвы принимаются условия |
0, что |
|
|
y |
|
соответствует непроникновению примесей в почву.
Для учета сопротивления лесного массива движению потока воздуха представим слой воздуха в растительном покрове сплошной средой и введем в
соответствии с рекомендациями [15] непрерывно распределенные объемные силы, действующих внутри рассматриваемого лесного участка.
В этом случае сопротивление движению воздуха определяется в уравнениях Навье - Стокса как массовая сила вида F cd S 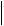V 
V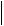
в пределах участка, занимаемого лесом. Здесь S - удельная плотность поверхности,
определяемая экспериментально, cd - коэффициент пропорциональности для сил сопротивления, зависящий от числа Рейнольдса, степени жесткости листьев, ветвей, геометрических размеров, форм и определяемый также экспериментально (табл. 6.1):
Таблица 6.1.
Зависимость коэффициентов S и cd от высота и типа лесного покрова [ 15 ]
Тип |
|
Характеристики |
|
покрова |
высота, м |
S, 1/м |
cd |
мелколиственны |
8 - 11 |
1,2 |
0,02 |
й лес |
|
|
|
сосна |
16 |
1,2 |
0,03 |
кукуруза |
2 - 3 |
3 - 6 |
0,17 |
бобовые |
1,2 |
7 |
0,05 |
164 |
|
|
|
культуры |
|
|
|
искусственный |
0,14 |
10 |
0,5 |
покров |
|
|
|
Выражение для силы сопротивления удобно представить в форме
F k(V ) V, |
k(V ) cd S V . |
Для построения следующего приближения решения поставленной ранее проблемы рассмотрим две связанные между собой задачи:
-движение потока газа по заданной области;
-рассеяние газовым потоком частиц примесей, находящихся в потоке,
причем при решении этой задачи используется поле скоростей, определенное решением первой подзадачи.
Для решения уравнений Навье - Стокса (6.10) и несжимаемости (6.11) с
начальными условиями (6.13) и граничными условиями (6.14) - (6.15) наиболее эффективен метод расщепления, при котором решение исходной задачи заменяется последовательностью решения ряда одномерных задач.
Введем обозначения:
2
Ax(u) u x x2 ,
2
Ay(v) v y y2 ,
fx |
1 |
p |
|
|
u |
|
k V u . |
|
|
|
x |
|
|
|
Первое уравнение системы (6.10) запишем в форме: |
|
|||
u Ax u u Ay v u fx u . |
(6.16) |
|||
t |
|
|
|
|
165
Пусть для некоторого момента времени t решение задачи u(t,x,y)
найдено. Тогда для следующего момента времени решение можно представить в виде:
|
u(t ,x,y) u(t,x,y) u(t,x,y) t O t2 |
|
|
|
|
|
||||
|
|
|
|
|
t |
|
|
|
|
|
|
u(t,x,y) Fx u Ax u u(t,x,y) Ay v u(t,x,y) O t2 |
|
||||||||
|
E tAx u tAy v u(t,x,y) tfx u O t2 . |
|
|
(6.17) |
||||||
|
Рассмотрим две вспомогательные задачи: |
|
|
|
||||||
u |
|
fx u1 , |
u1(t,x,y) u(t,x,y), |
u1(t,0,y) Vx G |
, |
u (t,L,y) |
0, |
|||
|
1 Ax u u1 |
1 |
||||||||
|
t |
|
|
|
|
|
|
|
x |
(6.18) |
|
|
|
|
|
|
|
u2 |
|
|
|
u2 |
Ay v u2 |
0, |
u2 (t,x,y) u1(t ,x,y), |
|
(t,x,H) |
|
||||
|
t |
u2(t,x,0) 0, |
|
0, |
|
|||||
|
|
|
|
|
|
|
|
y |
|
|
где L - ширина, H -высота участка, содержащего лесной массив.
Решение второй вспомогательной задачи для момента времени t t t
можно представить в форме
u2(t ,x,y) u2(t,x,y) u2 (t,x,y) t O t2 u2(t,x,y) tAy v u2(t,x,y) O t2
t
E tAy v u2(t,x,y) O t2 .
Учитывая начальные условия второй вспомогательной задачи, получаем:
|
|
|
|
|
|
|
|
|
|
O |
|
2 |
|
|
|
|
|
|
|
u2 |
(t ,x,y) |
|
E |
|
|
tAy v u1(t ,x,y) |
t |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
y |
|
|
1 |
u (t,x,y) |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
1 |
|
|
|
|
t2 |
|
|
||||||||
|
E tA |
v |
u (t,x,y) |
|
|
t O |
|
O t2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
E Ay v u1(t,x,y) Fx u1 Ax u u1(t,x,y) O 2 O 2
E Ay v E Ax u u1(t,x,y) fx u1 O 2 O 2 .
166
Перемножая слагаемые в скобках и пренебрегая всеми членами,
содержащие шаг по времени в степени выше, чем вторая, приходим к соотношению
u2 (t ,x,y) E tAy v E tAx u u1(t,x,y) tfx u1 O t2
E tAy v tAx u u1(t,x,y) tfx u1 O t2
E tAy v tAx u u(t,x,y) tfx u O t2 .
В последнем выражении учтены начальные условия первой вспомогательной задачи. Сравнивая полученный результат с выражением
(6.17), можно сделать вывод, что последовательное решение одномерных задач
(6.18) позволяет определить решение первого уравнения системы (6.10) с
погрешностью не выше, чем O( t2 ).
Аналогично показывается, что второе уравнение системы (6.10) также можно заменить последовательным решением двух вспомогательных дифференциальных уравнений
v
1 Ay v v1 fy v1 , v1(t,x,y) v(t,x,y), v1(t,x,0) 0,
t
|
|
Ax u v2 |
0, |
v2(t,x,y) v1(t ,x,y), |
v2(t,0,y) Vy G , |
v2 |
|||||
|
t |
|
|
|
|
v1(t,x,H) 0,
y
(6.19)
v2(t,L,y) 0,
x
с погрешностью не выше O( 2 ).
Для решения уравнения (6.11) используется метод Белоцерковского29 [17].
Для удовлетворения уравнения несжимаемости вводится дополнительное
давление p, определяемое из дифференциального уравнения
2 p |
|
2 p |
|
u |
2 |
v |
|
|
(6.20) |
|||
x |
2 |
y |
2 |
|
|
|
2 |
. |
||||
|
|
|
|
t |
x |
y |
|
|
||||
29 Белоцерковский Олег Михайлович [1925] - ученый в области механики, действительный член АН СССР с 1979 года. Основные работы выполнены в областях теоретической и прикладной аэродинамики, вычислительной математике.
167
Найденное таким образом поле p позволяет уточнить распределение
составляющих вектора скорости
|
u t ,x,y u2 t ,x,y |
t |
p x,y , |
|
v t ,x,y |
v2 t ,x,y t p x,y |
(6.21) |
||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
y |
|
|
|
и давления |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
p t,x,y |
p t,x,y p x,y . |
|
|
|
|
|
|
|||||||||
|
Для получения решения уравнения Пуассона используется метод |
||||||||||||||||
установления, когда поле p определяется |
как стационарное решение (® ) |
||||||||||||||||
нестационарного дифференциального уравнения параболического типа |
|||||||||||||||||
|
|
2 |
|
2 |
|
1 u |
|
v |
|
|
|
(6.22) |
|||||
|
|
|
|
2 |
|
y |
2 |
|
|
|
|
2 |
|
2 |
, |
|
|
|
|
x |
|
|
|
|
t |
x |
y |
|
|
|
|||||
где |
1 |
p, |
|
const . |
Величина |
параметра определяется |
из условия |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
эффективного управления устойчивостью вычислительного процесса. Решение уравнения (6.22) заменяется решением последовательности одномерных уравнений
|
1 |
2 |
1 |
|
1 u |
2 |
v |
2 |
|
, |
||
|
|
x2 |
|
|
|
|
||||||
|
|
|
|
|
t |
x |
y |
|
(6.23) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2 2
y2
сначальными
1 ,x,y ,x,y , 2 ,x,y 1 ,x,y
168