
Boyarshinov_ChM_T2
.pdf
h2
2 1 .
Для схемы Крэнка - Николсона условие устойчивости принимает вид
h2 .
Устойчивость по правой части имеет место в случае выполнения неравенства
1 |
2 |
|
2 |
|
|
, |
||
|
h |
2 |
|
h |
2 |
|
, 0 |
|
|
|
|
|
|
|
|
||
которое выполняется, например, при 1.
Рассмотренная схема имеет первый (или второй при = 1/2) порядок аппроксимации и является условно устойчивой по начальным данным и по правой части. Это означает, что семейство рассмотренных схем с весами дает последовательности численных решений, сходящихся к точному решению при уменьшении шагов t и h.
Трехслойная схема Ричардсона
Для уравнения (5.13) разностный аналог с использованием пятиточечного шаблона (рис. 5.4) записывается в виде:
uj uj |
uj 1 2uj |
uj 1 f j . |
(5.16) |
2 |
h2 |
|
|
Для оценки устойчивости этой разностной схемы воспользуемся методом Неймана. Предполагая, как и ранее, справедливым разложение возмущения в ряд Фурье, для k-гармоники
umj 1 k |
k m 1akeikxj , |
umj k |
k m akeikxj , |
umj 1 k |
k m 1akeikxj |
получаем (рассматривается возмущение только начальных данных; правая часть уравнения неизменна):
1 |
k |
m 1 k m 1 eikxj k m |
2 eikxj h 2eikxj eikxj h , |
2 |
|
|
h |
2k k |
2 2 e h 2 eh 1 0. |
|
|
h
 t
t
i+1 i
129

i-1
0
0 |
j-1 |
j |
j+1 |
x |
Рис. 5.4. Пятиточечный шаблон разностной схемы Ричардсона
Вспоминая формулу Эйлера, приходим к выражению
2 |
k |
8 |
sin |
2 |
kh |
1 0. |
||
k |
h |
2 |
|
|
|
|||
|
|
|
|
|
|
2 |
|
|
Корни этого квадратного уравнения
k |
4 |
sin |
2 |
kh |
|
16 2 2 |
sin |
4 |
kh |
1 |
||
|
|
|
|
h4 |
|
|
|
|||||
|
h2 |
|
|
|
2 |
|
|
|
|
2 |
|
|
вещественные, различные. Поскольку произведение корней
 k 1 k 2
k 1 k 2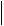 1,
1,
можно сделать вывод о том, что один из них превышает единицу. Но согласно формулировке теореме 4.5 это означает неустойчивость разностной схемы
(5.16).
Схема Дюфорта и Франкела
На том же шаблоне (рис. 5.4) построим другой разностный аналог уравнения (5.13):
uj |
|
uj |
|
|
|
1 |
uj |
|
|
fj . |
(5.17) |
||||||
|
2 |
h |
2 |
uj 1 2 |
2 |
uj |
uj 1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Погрешность аппроксимации этой разностной схемы |
|
||||||||||||||||
|
|
|
2 |
u˙˙˙ |
|
h2 |
u |
iv |
|
|
2 |
|
|
|
|
||
j |
6 |
j |
|
j |
h2 |
u˙˙ |
j |
|
|
||||||||
|
|
|
|
12 |
|
|
|
|
|
|
|
||||||
зависит от соотношения шагов интегрирования  h и мала лишь в случае
h и мала лишь в случае
lim 0.
,h 0 h
Как и в предыдущем случае, метод Неймана приводит к квадратному уравнению
2k |
k |
4 cos kh |
2 h2 |
0, |
|
|
2 h2 |
2 h2 |
|
анализ корней которого следует выполнить самостоятельно.
Схема бегущего счета
130
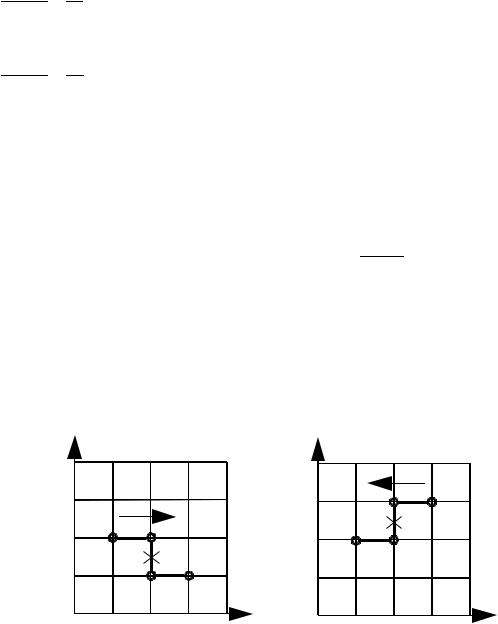
Для четных слоев (рис. 5.5а) разностная схема имеет вид:
uj |
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|||
uj |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
u |
|
u |
|
uj uj 1 |
|
f |
. |
(5.181) |
|||||
|
|
|
h2 |
j 1 |
|
|
j |
|
|
|
|
|
j |
|
|
|
||
Для нечетных (рис. 5.5б): |
|
|
~ |
|
|
|
|
|||||||||||
u |
|
u |
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
j |
|
|
uj |
|
~ |
|
(5.18 |
2 |
) |
||||||||
|
|
|
|
h |
2 uj 1 |
|
uj |
uj 1 |
|
f j . |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Значения функций в правой части разностных уравнений вычисляются в точках, указанных на рис. 5.5. Очевидным преимуществом этой схемы является то, что при формально неявном ее построении можно определить решение для следующего временного слоя без решения системы алгебраических уравнений, то есть явно. Для четных слоев расчеты выполняются с использованием схемы
(5.181) слева направо,
1 |
|
uj 1 |
|
|
1 |
|
|
~ |
, |
j 1,N 1. |
|||||||
uj |
|
2 |
|
h |
2 |
uj |
|
2 |
|
uj 1 |
h |
2 |
f j |
||||
|
h |
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
||
Поскольку значение u0 известно из граничного условия, из полученного соотношения можно определить u1. Затем, по найденному u1 вычисляется u2, и так далее, до конечного значения uN-1.
t
i+1
i
i-1
0
0 j-1 |
j |
j+1 |
x |
0 |
j-1 |
j |
j+1 |
x |
а |
|
|
|
|
|
б |
|
|
Рис. 5.5. Четырехточечные шаблоны разностной схемы бегущего счета; а - четные, б - нечетные слои
Аналогично производится процедура с использованием соотношения (5.182) для нечетных временных слоев, для чего расчеты выполняются справа налево. При известном граничном условии uN определяется значение uN-1, затем uN-2 и так далее:
131

|
1 |
|
uj 1 |
|
|
1 |
|
uj |
h2 |
||
uj |
|
h2 |
|
h2 |
uj |
|
h2 |
|
|
||
|
|
|
|
|
|
|
|
||||
~
~
f j , j N 11, .
Погрешность аппроксимации диференциального уравнения (5.13) разностными аналогами (5.18) зависит от соотношения шагов интегрирования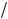 h, h, 3
h, h, 3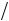 h, 4
h, 4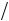 h2 . Благодаря взаимному сокращению погрешностей прямого и обратного ходов на последовательных слоях происходит частичная компенсация погрешностей. Поэтому общая погрешность аппроксимации для
h2 . Благодаря взаимному сокращению погрешностей прямого и обратного ходов на последовательных слоях происходит частичная компенсация погрешностей. Поэтому общая погрешность аппроксимации для
двух последовательных проходов определяется как O 2 h2 |
h . Схема |
обладает условной устойчивостью при h2 . |
|
Многомерные уравнения
Обратимся к дифференциальному уравнению параболического типа
|
|
2 |
u2 |
|
2 |
u2 |
|
|
|
|
|
t,x,y G |
(5.19) |
||||||
u |
|
|
f t,x,y , |
|
|||||||||||||||
t |
x |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
на прямоугольнике |
|
|
|
|
|
|
|
|
|
|
|||||||||
G 0 t T 0 x L 0 y H |
|
|
|||||||||||||||||
с краевыми условиями |
|
|
|
|
|
|
|
|
|||||||||||
u 0,x,y U0 x,y ; |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t,y , |
u t,L,y U2 t,y ; |
(5.20) |
||||||||||
u t,0,y U1 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
t,x,0 |
U |
|
, |
t,x,H |
U |
t,x |
. |
|
||||||||||
u |
|
|
|
t,x |
u |
|
|
|
|
||||||||||
Для области G построим разностную сетку
|
|
,xj |
,yk |
ti i ,i 0,m; |
xj j hx , j 0,n; |
|
ti |
yk k hy ,k 0,s , |
причем шаги интегрирования будем считать постоянными по каждой переменной, m T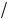 , n L
, n L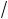 hx , s H
hx , s H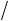 hy .
hy .
Введем обозначения:
|
|
|
|
ui 1j |
2uij |
ui 1j , |
|
xuij |
h |
2 |
|||||
|
|
|
x |
|
|
(5.21) |
|
|
|
|
|
|
|||
|
|
|
|
|
|
||
|
yuij |
|
uij 1 |
2uij |
uij 1 |
||
|
|
2 |
|||||
|
|
|
hy |
|
|
|
|
разностных операторов вторых производных по соответствующим направлениям.
Запишем разностный аналог с “весами” для дифференциального уравнения
uij |
uij xuij |
yuij 1 xuij |
yuij . |
(5.22) |
(5.19): |
|
|
|
|
1
В развернутой форме каждое разностное уравнение (5.22) 132
1 |
|
u |
u |
ij |
ui 1j |
2uij |
ui 1j |
|
uij 1 2uij |
uij 1 |
|
|
|
|
2 |
|
2 |
|
|
||||||
|
ij |
|
|
|
|
|
|
|
||||
|
|
|
|
|
hx |
|
|
hy |
|
|
|
|
2uij |
ui 1j |
|
uij 1 2uij |
uij 1 |
|
ui 1j |
|
|
||||
1 |
2 |
|
2 |
|
|
|
|
hx |
|
|
hy |
|
|
содержит пять неизвестных величин. Это означает, что для определения всех искомых величин в узлах сеточной области при очередном шаге по времени необходимо решить систему m 1 n 1 линейных алгебраических уравнений с соответствующими граничными условиями.
i-1 |
i |
t |
|
i+1
j+1
y 

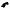

 j-1 j
j-1 j
x
Рис. 5.6. Шаблон для аппроксимации пространственного дифференциального уравнения параболического типа
Понятно, что в соответствии с принятой терминологией схема (5.22) при = 0 является явной, при = 1 - неявной. Погрешность аппроксимации дифференциального уравнения (5.19) схемой (5.22) имеет порядок O hx2 hy2
при произвольном значении коэффициента . В случае = 1/2 (схема Крэнка -
Николсона) порядок аппроксимации по шагу повышается до O 2 hx2 hy2 .
Схема (5.22) устойчива при выполнении условия
1 hx2hy2 .
2 hx2 hy2
Схема переменных направлений (продольно - поперечная схема)
133
Рассмотрим ряд экономичных разностных схем, существенно понижающих необходимые ресурсы вычислительной техники для нахождения решений пространственных задач (рис. 5.7).
Первый полушаг:
2 |
~ |
|
~ |
yuij |
~ |
(5.231) |
|
uij |
uij xuij |
fij . |
|||
|
|
|
|
|
|
|
Второй полушаг: |
|
|
||||
2 |
uij |
~ |
~ |
yuij |
~ |
(5.232) |
|
uij xuij |
fij . |
||||
|
|
|
|
|
|
|
Разностные операторы в этих уравнениях определяются формулой (5.21);
символ ~ (волна) относится к промежуточному временному слою tk 2 .
t |
tk+1 |
y i-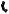
 1
1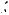



 i
i
i+1 j+1
j-1 tk
x
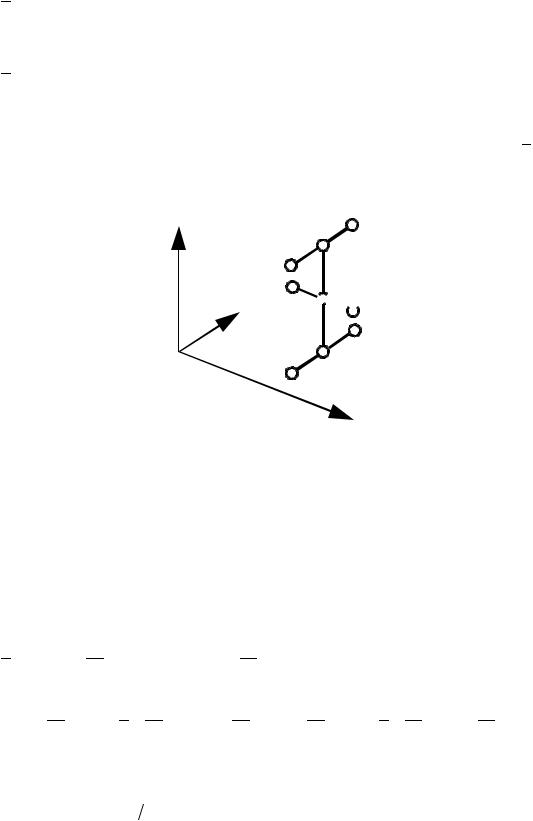
Рис. 5.7. Шаблон для аппроксимации пространственного дифференциального уравнения параболического типа схемой переменных направлений.
В полном виде разностная схема для первого полушага записывается следующим образом:
2 |
~ |
|
uij |
|
|
uij |
|||
|
|
|
|
|
~ |
|
|
|
|
u |
|
|
|
|
i 1j |
|
|
hx2 |
|
|
~ |
|
|
~ |
~ |
|
|
uij 1 |
|
|
|
|
|
~ |
|
|
|
|
|
|
|
2 |
ui 1j |
2uij |
ui 1j |
2 |
2uij uij 1 fij , |
|
|
|
|
|
|||||||||||
hx |
|
|
|
|
|
|
hy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ 1 |
|
|
~ |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
~ |
|||
|
|
|
|
|
|
|
|
|
|||||||||||||
2uij |
2 |
ui 1j |
|
2 |
uij |
1 |
2 |
2uij |
|
2 |
uij 1 |
2 |
fij . |
||||||||
|
|
|
hx |
|
|
|
hx |
|
|
hy |
|
|
|
hy |
|
hy |
|
|
|||
Последнее выражение представляет собой систему алгебраических уравнений относительно неизвестных значений искомой функции для
временного слоя tk |
2 |
, причем все неизвестные величины лежат вдоль одной |
координатной оси. |
Это |
означает, что вместо системы m 1 n 1 уравнений |
134

вида (5.22) на первом полушаге разностной схемы (5.231) следует решать n+1 систему, каждая из которых содержит по m+1 линейному алгебраическому уравнению, а на втором полушаге для схемы (5.232) - m+1 систему по n+1 линейному алгебраическому уравнению в каждой. Это приводит к существенной экономии вычислительных ресурсов, а кроме того позволяет распараллелить расчеты, то есть использовать преимущества транспьютерных и многопроцессорных вычислительных систем.
Для каждого полушага погрешность аппроксимации может быть оценена как O hx2 hy2 . На двух последовательных полушагах общая погрешность (за счет погашения погрешностей разного знака каждого полушага) составляет
O 2 hx2 hy2 . Разностная схема (5.23) безусловно устойчива по начальным данным и по правой части.
Метод расщепления
Пусть решение u t,x,y уравнения (5.19) известно для некоторого момента времени tk. Воспользуемся разложением решения в ряд Тейлора:
u tk 1 ,x,y u tk ,x,y u˙ tk ,x,y O 2 .
Обозначим:
Ax |
2 |
Ay |
|
2 |
|||
x |
2 , |
|
y |
2 , |
|||
|
|
|
|
|
|
||
2 |
2 |
|
|
|
|||
A |
|
2 |
y |
2 |
Ax Ay . |
||
x |
|
|
|
|
|
||
Теперь искомое решение с учетом выражения (5.19) можно записать в виде
u tk 1 ,x,y u tk ,x,y Au tk ,x,y O 2 E A u tk ,x,y O 2 . |
(5.24) |
||||||||
Рассмотрим вспомогательные задачи: |
|
|
|||||||
v 2v A v, |
v t |
|
,x,y u t |
|
,x,y , |
|
(5.25) |
||
t |
x2 |
x |
|
k |
|
k |
|
|
|
w |
2w |
Ayw, |
w tk ,x,y v tk 1 ,x,y . |
|
(5.26) |
||||
t |
x2 |
|
|
|
|
|
|
|
|
В задаче (5.25) начальным условием на отрезке tk ,tk 1 |
для функции v t,x,y |
||||||||
выступает известное решение u tk ,x,y ; в задаче (5.26) начальным условием для на том же отрезке - найденная из решения задачи (5.25) функция
v tk 1,x,y .
Ряд Тейлора для функции w t,x,y :
w tk 1 ,x,y w tk ,x,y w˙ tk ,x,y O 2 .
Принимая во внимание уравнение (5.26) с начальным условием, получаем:
135
w tk 1 ,x,y w tk ,x,y w˙ tk ,x,y O 2 w tk ,x,y Ayw tk ,x,y O 2
E Ay w tk ,x,y O 2 E Ay v tk 1 ,x,y O 2 .
Для дальнейших преобразований воспользуемся уравнением (5.26) с соответствующим начальным условием:
w tk 1 ,x,y E Ay v tk ,x,y v˙ tk ,x,y O 2 O 2
E Ay E Ax v tk ,x,y O 2 O 2 .
Раскрываем скобки и собираем все слагаемые, содержащие шаг интегрирования t в степени не ниже второй:
w tk 1 ,x,y E Ay Ax 2 Ax Ay v tk ,x,y O 2
E Ay Ax u tk ,x,y O 2 E A u tk ,x,y O 2 .
Сравнение последнего выражения с соотношением (5.24) позволяет сделать вывод, что
w tk 1 ,x,y u tk ,x,y O 2 .
Это означает, что последовательное решение двух одномерных задач (5.25) и (5.26) с соответствующими начальными условиями позволяет получить решение исходной двумерной задачи (5.19) с точностью до O 2 .
Контрольные вопросы и задания
Покажите условия сопряжения граничных и начальных условий (5.14).
Покажите условия существования и единственности решения системы уравнений (5.15). Воспользуйтесь для анализа теоремой 3.1.
Определите порядок аппроксимации диференциального уравнения (5.13) разностной схемой (5.16).
Оцените порядок аппроксимации диференциального уравнения (5.13) разностной схемой (5.17) и убедитесь в ее безусловной устойчивости.
Оцените порядок аппроксимации диференциального уравнения (5.13) разностной схемой (5.18) и условия ее устойчивости.
Запишите условия сопряжения для краевых условий (5.20).
Проверьте порядок аппроксимации схемой (5.22) диференциального уравнения (5.19) и условия ее устойчивости. Определите условия устойчивости этой схемы в случае использования варианта Крэнка - Николсона.
136
Проверьте порядок аппроксимации схемой (5.23) диференциального уравнения (5.19) на каждом полушаге и для всего шага, а также условия ее устойчивости.
Предложите варианты замены одномерных дифференциальных задач (5.25) и (5.26), аппроксимирующих двумерную задачу (5.19), разностными схемами. Оцените их порядки аппроксимации и условия устойчивости.
Определите условия устойчивости схемы Крэнка - Николсона с помощью метода Неймана.
137
