Boyarshinov_ChM_T2

Поскольку выражение в первой скобке обращается в нуль в силу уравнения (5.1), становится очевидным, что невязка пропорциональна первым степеням шагов по времени и координате. Используя чебышевскую норму, получаем

откуда следует, что рассмотренная разностная схема имеет первый порядок погрешности при аппроксимации дифференциального уравнения.

Оценку устойчивости проведем с помощью принципа максимума. Для этого разностную схему (5.3) запишем в виде

119

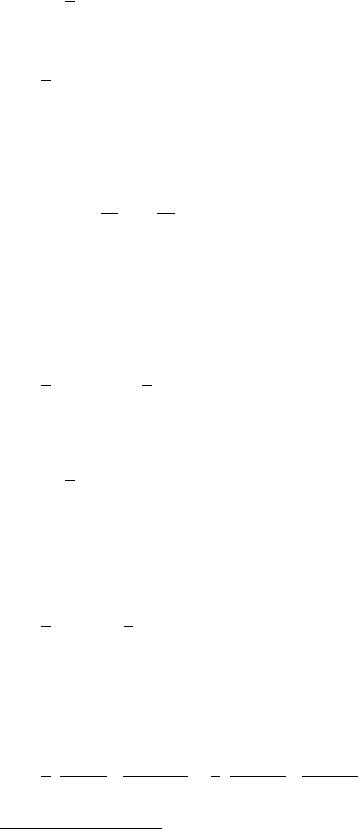
Разностная схема условно устойчива при выполнении условия Куранта23, ограничивающего шаги интегрирования:

Устойчивость по правой части имеет место при выполнении условия

1,

что справедливо, например, при 1.

Из выражения (5.4) следует разрешимость и единственность решения разностного уравнения (5.3):

Согласно теореме 4.4 численное решение задачи (5.1) - (5.2) на разностной схеме (5.3) будет сходиться к точному решению при выполнении соотношения (5.5) и уменьшении шагов по времени и координате ( h, t ® 0 ).

Вторая разностная схема, соответствующая шаблону, показанному на рис. 5.1б, приводит к разностному соотношению

и также имеет погрешность аппроксимации O(h+t). Условие устойчивости по начальным данным в этом случае записывается иначе:

Условие устойчивости по правой части также выполнено. Это позволяет утверждать, что последовательность численных решений, получаемых при уменьшающихся шагах интегрирования h и t также сходится к точному.

Разностная схема, получаемая для шаблона, изображенного на рис. 5.1в,

оказывается безусловно устойчивой по начальным данным и правой части, и имеет также первый порядок аппроксимации.

Шаблон, показанный на рис. 5.1д, приводит к разностному аналогу дифференциального уравнения (5.1)

23 Курант Рихард [8.1.1888 - 27.1.1972] - математик, учился в университетах Бреслау и Цюриха. Профессор Геттингенского университета с 1920 по 1933 годы, професор Нью-Йоркского университета с 1934 года.Основные научные труды выполнены в теории конформных отображений и для краевых задач математической физики. Избран в 1966 году иностранным членом Академии наук СССР.

120

имеющему второй порядок аппроксимации и безусловно устойчивому по начальным данным и правой части.

Формально разностные схемы, получаемые для шаблонов, изображенных на рис. 5.1а и 5.1г, являются явными, а на рис. 5.1б, 5.1в и 5.1д - неявными. В то же время в трех последних случаях можно явно вычислить значение uj .

Действительно, крайнее левое значение u0 U0 t известно из граничного условия (5.2). Следовательно, можно вычислить u1, рассматривая разностную схему как уравнение с одним неизвестным. Далее можно вычислить u2 , пользуясь разностным уравнением, записанным для следующего узла, и так далее для всех остальных узлов сетки.

Схема (5.9) имеет второй порядок аппроксимации и при не слишком больших шагах h и дает более точное решение. Однако на быстропеременных решениях точность этой схемы понижается. В этом случае лучшие результаты получаются на схемах (5.3), (5.6) и (5.8).

Разностная схема (5.8) безусловно устойчива, что имеет преимущество при проведении вычислительного эксперимента. В то же время схемы (5.3) и (5.6) являются более точными.

Явно-неявная схема

Пусть шаги интегрирования h и являются переменными, а скорость движения частицы v(t, x) зависит от времени t и координаты x. В этом случае при использовании разностных схем (5.3) и (5.6) для выполнения очередного шага интегрирования необходимо выполнения условия Куранта для устойчивости процесса вычислений. Целесообразно строить вычислительный процесс следующим образом: если выполняется условие (5.5), то очередное значение uj определять из разностной схемы (5.3); при справедливости условия (5.7) вычисления выполнять по формуле (5.6). Это гарантирует устойчивость явно-неявной схемы; следует отметить ее более высокую точность по сравнению со схемой (5.8).

Многомерное уравнение переноса

Рассмотрим аналогичную задачу с двумя пространственными переменными:

с краевыми условиями

121

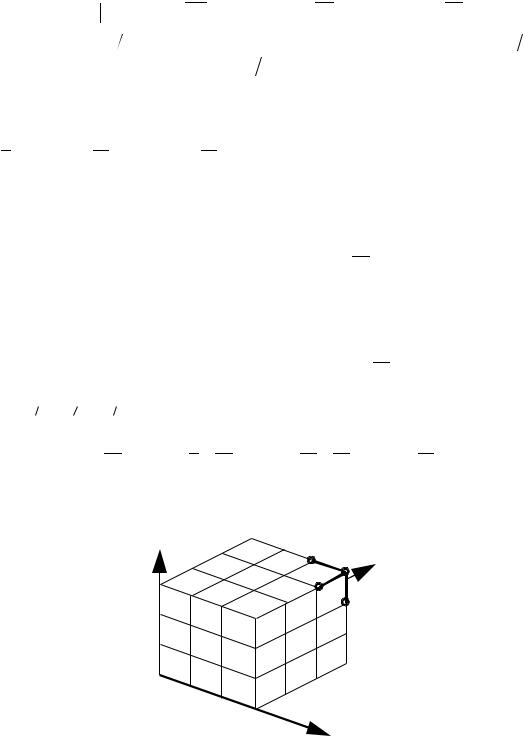
Рассмотрим разностный аналог дифференциального уравнения (5.10), построенный в соответствии с шаблоном, показанным на рис. 5.2:

t

y

i

i-1

k

k-1

j-1

j

122

x

Рис. 5.2. Шаблон для двумерного уравнения переноса.

Подставим эти разложения в разностный аналог (5.12):

fx ti ,xj ,yk h2x fy ti ,xj ,yk h2y O 2 ,hx2 ,hy2

u˙ ti ,xj ,yk ux ti ,xj ,yk vx uy ti ,xj ,yk vy f ti ,xj ,yk

hy fy ti ,xj ,yk uyy ti ,xj ,yk O hx hy .

2

Это означает, что разностная схема (5.12) имеет первый порядок аппроксимации.

Представим выражение (5.12) в виде алгебраического уравнения:

В соответствии с принципом максимума условие устойчивости по начальным данным требует выполнения неравенства

которое справедливо при любых соотношениях шагов интегрирования. Следовательно по начальным данным схема (5.12) безусловно устойчива.

Устойчивость по правой части также имеет место:

Общий вывод: разностная схема (5.12) имеет первый порядок аппроксимации, безусловно устойчива по начальным данным и правой части.

123

Последовательность численных решений сходится к точному решению задачи (5.10) - (5.11) при уменьшающихся шагах интегрирования.

Контрольные вопросы и задания

Проверьте условия устойчивости по начальным данным и правой части, а также порядок аппроксимации разностной схемы (5.6) диференциального уравнения (5.1).

Проверьте условия устойчивости по начальным данным и правой части, а также порядок аппроксимации разностной схемы (5.6) диференциального уравнения (5.1) в случае, когда v < 0.

Проверьте условия устойчивости по начальным данным и правой части, а также порядок аппроксимации разностной схемы (5.8) диференциального уравнения (5.1).

Проверьте условия устойчивости по начальным данным и правой части, а также порядок аппроксимации разностной схемы (5.8) диференциального уравнения (5.1) в случае, когда v < 0.

Установите условия устойчивости по начальным данным и правой части, а также порядок аппроксимации дифференциального уравнения (5.1) разностной схемой, получаемой для шаблона, изображенного на рис. 5.1г.

Установите условия устойчивости по начальным данным и правой части, а также порядок аппроксимации дифференциального уравнения (5.1) разностной схемой, получаемой для шаблона, изображенного на рис. 5.1г для случая, когда v < 0.

Определите условия устойчивости по начальным данным и правой части, а также порядок аппроксимации разностной схемы (5.9) диференциального уравнения (5.1). Разложение точного решения в ряд Тейлора в этом случае целесообразно производить для окресности центра ячейки.

Определите условия устойчивости по начальным данным и правой части, а также порядок аппроксимации разностной схемы (5.9) диференциального уравнения (5.1) для случая v < 0. Воспользуйтесь указанием к предыдущему заданию.

Укажите условия сопряжения краевых условий (5.11).

124

описывающее процессы теплопроводности ( играет роль коэффициента температуропроводности) в тонком однородном стержне, либо диффузии ( - коэффициент диффузии).

Схема с “весами”

t

i+1

i

0

Рис. 5.3. Шеститочечный шаблон для аппроксимации одномерного дифференциального уравнения параболического типа.

Ранее уже были рассмотрены явный (4.16) и неявный (4.18) разностные аналоги такого дифференциального уравнения и выявлены некоторые их свойства. Теперь рассмотрим еще один распространенный шаблон для аппроксимации дифференциального уравнения (5.13), показанный на рис. 5.3:

126

Очевидно, что при = 0 разностная схема (5.15) становится явной, при = 1 она переходит в неявную. Проверим порядок аппроксимации исходного уравнения (5.13) разностным аналогом (5.15). Воспользуемся разложениями точного решения в ряды Тейлора24 возле точки ti ,xj :

u ti 1 ,xj 1 u ti ,xj u˙ ti ,xj u ti ,xj h 21 u˙˙ ti ,xj 2 2u˙ ti ,xj h u ti ,xj h2

Невязка, получаемая в результате подстановки этих разложений в формулу

(5.15):

С учетом уравнения (5.13) это выражение дает оценку

24 Ряд Тейлора для функций нескольких переменных (кратный ряд):

127

h2 uiv ti ,xj O 3 ,h3 O h2 ,

12

то есть имеет место погрешность аппроксимации первого порядка по шагу и второго порядка по шагу h.

Дополнительно продифференцируем по переменной t выражение (5.13):

до второго порядка по обоим шагам интегрирования. Полученная схема интегрирования дифференциального уравнения (5.13) с весовым

коэффициентом 1 носит название схемы Крэнка - Николсона.

2

Для оценки устойчивости разностной схемы преобразуем выражение (5.15) к виду:

Положим

12

max h2 .

Согласно принципу максимума, для устойчивости решения по начальным данным должно выполняться условие:

128