Boyarshinov_ChM_T2

Уравнения гиперболического типа

Рассмотрим уже упоминавшееся дифференциальное уравнение гиперболического типа, которое описывает механические колебания тонкой однородной струны плотностью , растянутой усилием F:

с заданными начальными

и граничными условиями

Схема “крест”

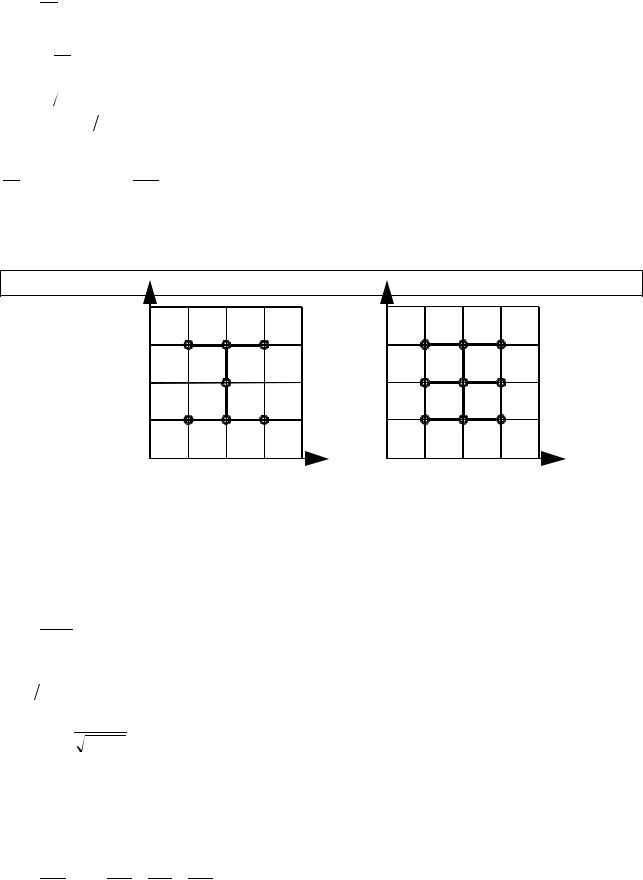
Для построения разностного аналога дифференциального уравнения (5.27) используем шаблон, представленный на рис. 5.4 :

Оценим погрешность аппроксимации уравнения (5.27) этой разностной

схемой с помощью рядов Тейлора:

139

Заменяя узловые значения в выражении (5.30) с помощью этих

соотношений, получаем:

Учитывая исходное уравнение (5.27), получаем:

Теперь становится очевидным, что погрешность аппроксимации

ij O h2 2

имеет второй порядок относительно шагов интегрирования и h.

Понятно, что полученная явная разностная схема (5.30) является трехслойной. В начальный момент времени (t = 0) решение известно из начального условия (5.28). Для следующего временного слоя (t = ), используя второе начальное условие, получаем выражение

1 uj U xj V xj ,

из которого следует соотношение для нахождения решения на втором временном слое:

Теперь, зная решение для двух слоев, можно с помощью формул (5.30) найти искомые узловые значения uj для третьего слоя, и так далее.

Нетрудно показать, что формула (5.31) дает первый порядок

140

Для оценки устойчивости схемы (5.30) по отношению к возмущению начальных данных воспользуемся методом Неймана. Разностная схема, записанная относительно погрешностей имеет вид:

Положим, как и ранее,

uj akeikxj ,

uj k uj kakeikxj ,

uj 2k uj 2kakeikxj .

Подстановка этих формул в предыдущее выражение приводит к

соотношению

Учитывая, что

e ikh 2 eikh 4sin2 kh2 ,

получаем квадратное уравнение относительно коэффициента роста гармоник

Корни этого уравнения равны

141

(5.33)

t

Рис. 5.8. Шаблоны с “весами” для аппроксимации одномерного дифференциального уравнения гиперболического типа.

Устойчивость рассмотренных схем по начальным данным имеет место при выполнении условия

Многомерные уравнения

Исследуем пространственное уравнение гиперболического типа, частным случаем которого является выражение (5.27):

с начальными

143

причем шаги интегрирования будем считать постоянными по каждому направлению,

Tm, hx Ln, hy Hs, hz Wp.

Введем обозначения:

для разностных операторов вторых производных по соответсвующим направлениям.

Рис. 5.9. Шаблон для аппроксимации пространственного дифференциального уравнения гиперболического типа.

Разностный аналог для пространственного дифференциального уравнения

(5.36):

Порядок аппроксимации этой схемой дифференциального уравнения (5.36) определяется выражением O 2 hx2 hy2 hz2 .

Решение разностного уравнения (5.40) устойчиво при выполнении обощенного критерия Куранта

144

1

Факторизация разностной схемы с “весами”

Рассмотрим разностный аналог дифференциального уравнения (5.36):

С учетом этого выражение (5.42) можно представить как систему линейных алгебраических уравнений относительно искомых узловых значений

uijk :

Buijk .

Рассмотрим произведение трех операторов:

E 2 x E 2 y E 2 z E 2 x 2 y 2 z O 4 B O 4 .

145

и перепишем полученное выражение в виде трех систем алгебраических уравнений:

E 2 x W ,

Решая последоватеьно эти три системы уравнений, получаем искомое решение - узловые значения uijk .

Факторизованная система имеет порядок аппроксимации O 2 hx2 hy2 hz2 .

Условие устойчивости:

Очевидно, что при весовом коэффициенте 14 имеет место безусловная устойчивость разностной схемы.

Контрольные вопросы и задания

Полагая f(t, x) = 0 в уравнении (5.27), определите, при каком условии порядок его аппроксимации схемой (5.30) становится ij O h4 4 .

Оцените порядок аппроксимации разностными схемами (5.31) и (5.32)

Оцените порядок аппроксимации дифференциального уравнения (5.27) разностной схемой (5.33) и проверьте условие (5.35) ее устойчивости.

Оцените порядок аппроксимации разностной схемой (5.34) дифференциального уравнения (5.27) и проверьте условие (5.35) ее устойчивости.

Оцените порядок аппроксимации разностной схемой (5.40) дифференциального уравнения (5.36) и проверьте условие (5.41) ее устойчивости.

Оцените порядок аппроксимации разностной схемой (5.42) дифференциального уравнения (5.36) и определите условие ее устойчивости.

Поясните геометрический (физический) смысл замены системы уравнений (5.42) системой уравнений (5.44).

146

Уравнения эллиптического типа

Для двумерного уравнения Пуассона26

рассмотрим задачу: найти функцию u(x,y), непрерывную вместе со своими производными второго порядка, удовлетворяющую уравнению (5.45) в области G и граничным условиям

- первого рода

Последнее выражение можно представить как смешанное граничное условие, включающее комбинацию условий первого и второго родов:

С помощью пятиточечного шаблона “крест”, изображенного на рис. 5.10, для всех внутренних точек сеточной области

26 Симеон Дени Пуассон [21.6.1781 - 25.4.1840] - французкий механик, физик, математик. Закончил Политехническую школу в Париже в 1800 году, с 1806 года - преподаватель этой школы. В 1809 году становится профессором Парижского университета. С 1812 года - член Парижской академии наук. В 1826 году избран иностранным почетным членом Петербургской академии наук.

148