Boyarshinov_ChM_T2

В частном случае для системы (2.17) имеет место

Метод Эйлера для системы дифференциальных уравнений

Рассмотрим первое уравнение системы (2.18):

du1 f1 x,u1,u2, ,un . dx

Разложим решение этого уравнения в ряд Тэйлора вблизи точки xp :

u1 xp 1 u1 xp u1 xp h O h2 u1 xp f1 xp,u1 xp , ,un xp h O h2 .

Схема Эйлера для этого уравнения принимает вид:

u1p 1 u1p f1 xp,u1p, ,unp h.

Для всей системы уравнений (2.18) схема метода Эйлера выглядит аналогично:

up 1 up f xp,u1p, ,unp h.

условиями является функция y x cos x . Первая производная решения равна y x sin x .

На фазовой плоскости (то есть в системе координат y y ) решение представляет собой окружность единичного радиуса, поскольку y2 y 2 cos2 x sin2 x 1. Этот частный факт можно использовать для оценки погрешности получаемого численного решения задачи.

Введем обозначения:

y x u1 x , y x u2 x .

Теперь исходную задачу можно представить в виде системы дифференциальных уравнений первого порядка с соответсвующими начальными условиями:

u1 u2 ,u2 u1

31

Разностная схема для этой системы уравнений записывается следующим образом:

u1p 1 u1p u2p h ,

u2p 1 u2p u1p h .

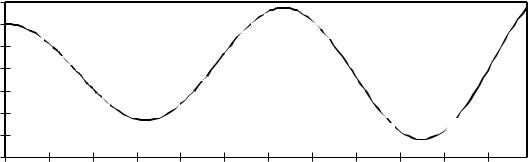
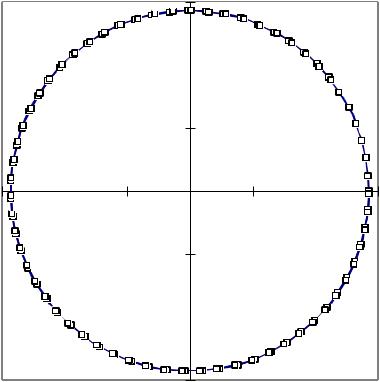
На рис. 2.4 приведен график численного решения y(x), полученный при шаге интегрирования h = 0.1. Поведение полученного решения на фазовой плоскости представлено на рис. 2.5. На рис. 2.6 показана зависимость погрешности численного решения, определяемой как отклонение от единичной окружности, в зависимости от значения аргумента.

Метод Рунге-Кутты для системы дифференциальных уравнений

Рассмотрим наиболее распространенную схему четвертого порядка точности.

Введем матрицы

32

33

up 1 up h6 K1 2 K2 2 K3 K4 .

На рис. 2.7 приведен график фазовой траектории численного решения задачи из примера 2.7, полученный для такого же шага интегрирования по приведенной схеме метода Рунге-Кутты. В этом случае отклонение получаемой траектории от окружности невелико и для всего участка интегрирования [0, 12] не превосходит 082536. 10 6 . Это вновь подтверждает, что схемы четвертого порядка аппроксимации имеют существенное преимущество в точности решения перед схемами первого порядка.

Разностные схемы интегрирования дифференциальных уравнений второго порядка

Рассмотрим дифференциальное уранение второго порядка

d2u f x,u,u dx2

с начальными условиями

34

Рис. 2.7. Фазовая диаграмма результатов численного решения уравнения y y 0 методом Рунге-Кутта четвертого порядка; шаг интегрирования 0.1 .

dv

f x,u,v ,

dx

Схема Эйлера (2.6) для рассматриваемого частного случая имеет вид:

vk 1 vk h f xk ,uk ,vk ,uk 1 uk h vk .

Рассмотрим некотрые варианты изменения этой схемы, представленные в книге [6]. В частности, модификация этой схемы, носящая название Эйлера-

Кромера,

vk 1 vk h f xk ,uk ,vk ,

uk 1 uk 1 h vk

дает устойчивые решения для колебательных систем.

35

Метод средней точки

имеет второй порядок точности по переменной u и первый порядок - по переменной v . Хотя приближение по средней точке дает точное решение при f = const, в общем случае он не приводит к значительно лучшим результатам по сравнению с методом Эйлера.

Несложные преобразования приводят к выражению

Метод полушага

vk 1/2 vk 1/2 h f xk ,uk ,vk ,uk 1 uk h vk 1/2

относится к методам высокой точности. Отметим, что этот метод относится к несамостартующим, поскольку значение v 1/2 в первом выражении для n = 0 не определено. Вместе с тем для начала вычислений можно положить

вычислить значение

u1 u0 h v1/2

и далее уже продолжать вычисления по приведенным формулам.

Теперь воспользуемся разложениями решения в ряды Тэйлора

Последовательно складывая и вычитая эти формулы, получаем:

u xk 1 u xk 1 2u xk h2u xk O h3 ,

u xk 1 u xk 1 2h u xk O h3 .

Используя полученные выражения, можно построить следующие соотношения:

36

uk 1 uk 1 2uk h2f xk ,uk ,vk ,

носящие название алгоритма Верле.

Очевидным недостатком этой схемы является то, что для начала расчетов необходимо знать два значения искомой функции, то есть схема является также несамостартующей. Премуществом является то, что схема Верле относится к схемам третьего порядка точности по переменной u и второго порядка по переменной v. Эта схема особенно эффективна, когда правая часть исходного уравнения не зависит от v.

Эквивалентной в некотором смысле этому алгоритму является

самостартующая схема

Точность такого же порядка, что и алгоритм Верле, имеет схема Бимана:

Контрольные вопросы и задания

Показано, что схема Рунге-Кутты (2.11) имеет второй порядок аппроксимации независимо от величины параметра . Однако при значении =0 эта схема обращается в схему Эйлера, имеющую первый порядок аппроксимации. Объясните причину противоречия.

Оцените порядок аппроксимации уравнения (2.1) неявной разностной схемой (2.14).

С помощью математических выкладок получите соотношения разностной схемы (2.20) из выражений (2.19).

При каких условиях схема (2.21) является явной?

Оцените порядок аппроксимации уравнения разностными схемами Эйлера-Кромера, Верле, Бимана, методами средней точки, полушага.

37

Дано дифференциальное уравнение y 1 y2 с начальным условием y(0) = 0.5. Оцените, сколько итераций метода Пикара и величины шагов интегрирования h в методах Эйлера, Рунге-Кутты второго, третьего и четвертого порядков, Адамса требуются для получения решения при х = 1, отличающегося от точного не более чем на

0.0001%.

Установите геометрический смысл одной из схем Рунге-Кутты третьго или четвертого порядков аппроксимации.

Определите условия, накладываемые на шаг интегрирования h в методе Рунге-Кутты второго порядка требованием невозрастания погрешности при выполнеии расчетов.

При оценке порядка аппроксимации дифференциального уравнения разностной

схемой Эйлера получено выражение k y xk h O h , значение которого

зависит не только от h, но и от величины y xk . Укажите условия, при которых

значение y xk ограничено. Каковы аналогичные условия для методов Рунге-

Кутты и неявной схемы аппроксимации?

38

3 . Г Р А Н И Ч Н Ы Е З А Д А Ч И Д Л Я О Б Ы К Н О В Е Н Н Ы Х

Д И Ф Ф Е Р Е Н Ц И А Л Ь Н Ы Х У Р А В Н Е Н И Й

В отличие от задач с начальными условиями в граничных задачах условия для определения постоянных интегрирования задаются в нескольких различных точках отрезка, на котором ищется решение исходной дифференциальной задачи. В качестве примера рассмотрим ряд постановок таких задач.

Пусть движение точки вдоль прямой описывается уравнением

причем известно, что к моменту времени Т точка прошла расстояние L; необходимо найти закон движения точки. Очевидно, что условия для нахождения постоянных интегрирования в рассматриваемом случае заданы для разных моментов времени и могут быть записаны в виде: x(0) = 0, x(T) = L.

q(x)

x

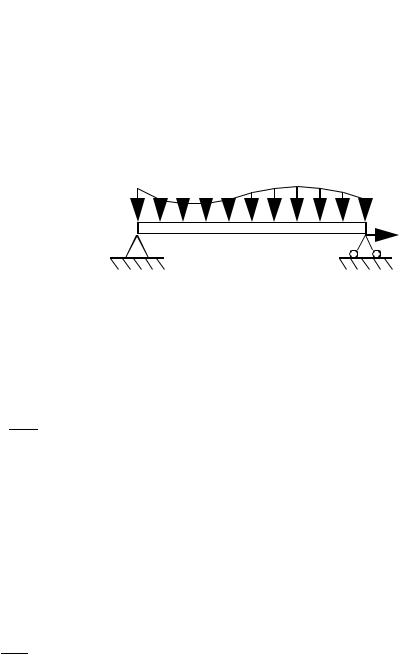
Рис. 3.1. Схема изгиба балки под действием перерезывающей нагрузки.

Неподвижная горизонтальная балка закреплена на опорах и испытывает действие распределенной по ее длине перерезывающей нагрузки. Уравнение изгиба балки имеет вид

EI d2w M x , dx2

Е - модуль упругости материала, I - момент инерции поперечного сечения балки, w(x) - функция прогибов, М(х) - переменный изгибающий момент от действия поперечных нагрузок. Шарнирные закрепления балки на опорах означают, что прогибы в ее крайних точках равны нулю, то есть w(0) = 0, w(L) = 0.

Температурное поле q(x) в стержне, теплоизолированном с боковой поверхности, описывается уравнением одномерной теплопроводности

d2q J x,q 0, dx2

41

где l - коэффициент теплопроводности, J(x,q) - мощность внутренних тепловых источников. Пусть на левом торце стержня поддерживается постоянная температура q 0 q0 , а на правом торце происходит теплообмен с

поверхности стрежня в окружающую среду; qcp - температура окружающей среды. Иначе последнее условие может быть записано в виде смешанного граничного условия q L q L cp .

Поскольку обыкновенное дифференциальное уравнение порядка n можно представить в виде системы n обыкновенных дифференциальных уравнений первого порядка, в общем случае постановка граничной задачи выглядит

Положим u1 a D. Из первого граничного условия 1 D,u2 a 0, как из уравнения, определим u2 a;D . Теперь значения

u1 a D,

(3.5)

u2 a;D

можно рассматривать как начальные условия для исходной системы дифференциальных уравнений, то есть вместо граничной задачи получили задачу Коши.

Решая каким-либо известным способом задачу (3.3), (3.5), находим решения u1 x;D , u2 x;D как функции параметра D. Очевидно, что второе граничное условие (1.25) в общем случае не будет выполнено из-за произвола в

42