Boyarshinov_ChM_T2

Ограничимся значением n = 3. Система уравнений (3.25) принимает вид:

разложения решения в ряд по пробным функциям:

y3 x 0 a1 1 a2 2 a3 3

Полученное решение является точным для поставленной задачи. Этим, в частности, объясняются значения a2 , a3 , равные нулю.

Разрешимость системы алгебраических уравнений метода Галеркина

Рассмотрим условия существования и единственности решения системы алгебраических уравнений (3.25), полученной в результате применения метода Галеркина к задаче (3.22) - (3.23).

Теорема 3.2. Пусть коэффициенты дифференциального уравнения (3.22) удовлетворяют условиям:

Тогда система алгебраических уравнений метода Галеркина (3.25) имеет единственное решение.

В однородную систему уравнений, соответствующую системе уравнений

(3.25),

65

b

подставим полученные ранее значения коэффициентов Cjk p k j q k j dx

Обозначим

n

zn bk k . k 1

Тогда предыдущее равенство можно записать в виде:

Домножим каждое из этих выражений на множитель bj и все полученные соотношения просуммируем:

При выполнении условий (3.27) последнее выражение справедливо лишь в том случае, когда zn x 0. Это означает, что функция

n

zn x bk k x const .

k 1

означает, что однородная система алгебраических уравнений (3.28) имеет только тривиальное решение, то есть ее определитель отличен от нуля, что и говорит о существовании единственного решения исходной системы уравнений

(3.25).

66

Метод наименьших квадратов

Рассмотрим линейное дифференциальное уравнение второго порядка

условиям, перечисленным в методе моментов. Это позволяет представить решение задачи (3.29) - (3.30) в виде разложения (3.20) в ряд по этим функциям.

Подстановка выражения (3.20) в уравнение (3.29) дает невязку

n x yn x p x yn x q x yn x f x 0,

величина которой зависит от значений выбранных коэффициентов ak , k 1,2,

Определим функционал

b

yn 2n x dx ,

69

a

Обозначим:

b

Сjk k p k q k j p j q j dx ,

a

b

fj f x 0 p 0 q 0 j p j q j dx .

a

Теперь систему уравнений (3.31) можно представить в виде системы линейных алгебраических уравнений относительно искомых коэффициентов разложения решения в ряд по пробным функциям

Легко заметить, что эта система уравнений имеет симметричную матрицу коэффициентов, Cjk Ckj .

Пример 3.6. Вновь рассмотрим одномерное уравнение стационарной теплопроводности

с граничными условиями

0 0, 1 1.

Возьмем систему пробных функций аналогичную рассмотренной в примере 3.4 :

0 x 0 1 0 x .

1 x x 1 x,

2 x x 1 x2 ,

3 x x 1 x3 ,

k x x 1 x k .

Ограничим число слагаемых в разложении (3.20) величиной n = 3. В этом случае коэффициенты системы уравнений (3.32) принимают значения:

70

Подставим сюда значения коэффициентов Сjk :

a

71

n

Здесь вновь обозначено: zn bk k . Умножим каждую из предыдущих

k 1

формул на bj и просуммируем все полученные выражения:

zn pzn qzn zn pzn qzn dx zn pzn qzn 2 dx 0 .

a a

Очевидно, что последнее равенство возможно лишь в случае, когда

Предположим, что граничная задача (3.33) - (3.34) имеет только

n

тривиальное решение zn bk k 0. В силу линейной независимости пробных

k 1

функций это возможно лишь при условии bk 0, k 1,n, то есть вспомогательная однородная система алгебраических уравнений имеет только тривиальное решение. Отсюда следует, что определитель этой системы уравнений отличен от нуля, что является необходимым и достаточным условием ее разрешимости. Проведенный анализ разрешимости метода наименьших квадратов может быть сформулирован в виде следующего утверждения.

Теорема 3.2. Если однородная граничная задача (3.33) - (3.34), соответствующая исходной граничной задаче (3.29) - (3.30), имеет только тривиальное решение zn 0, то система алгебраических уравнений (3.32) метода наименьших квадратов имеет единственное решение.

Сходимость метода наименьших квадратов

Рассмотрим граничную задачу (3.29) при упрощенных граничных условиях

72

- n-е приближение11 к точному решению, получаемое методом наименьших квадратов. Обозначим:

L z z p x z q x z.

Теорема 3.3. Последовательность функций yn x , получаемых по методу наименьших квадратов, сходится по метрике12 L2 к точному решению y(x), если выполнены условия:

а) граничная задача (3.29), (3.35) имеет единственное решение y(x);

Это выражение записано в обозначениях, использованных ранее при построении соотношений метода наименьших квадратов. Учтем, что при

11Очевидно, что при граничных условиях (3.35) пробную функцию 0 можно использовать наряду с остальными для получения приближения yn.

12Согласно [10], пространство L2 - совокупность всех вещественных измеримых функций, заданных и

b

скалярное произведение x,y axy dt .

73

использовании этого метода коэффициенты разложения (3.20) находятся из

k 1

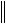L yn L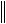 y L yn y .

В силу условия б)

L yn y Myn y.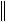

Поскольку может быть сделано как угодно мало,

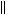yn y 0,

n

что и требовалось доказать.

Метод Ритца13

Пусть линейное дифференциальное уравнение второго порядка (3.22) с граничными условиями (3.23) имеет единственное решение.

Рассмотрим функционал

a

для которого будем искать минимальное значение на множестве допустимых функций, которые

а) непрерывно дифференцируемы на отрезке [a, b];

б) удовлетворяют граничным условиям (3.23).

Теорема 3.4. Если функция ~ доставляет минимальное значение y

x

функционалу (3.38) среди всех допустимых функций, то она является решением граничной задачи (3.22) - (3.23).

74

Отсюда получаем выражение

p x y q x y f x ,

которое полностью совпадает с исходным уравнением (3.22). Это означает, что

функция ~ x , удовлетворяющая граничным условиям (3.23), и на которой y

достигается минимум функционала (3.38), будет решением исходной задачи.

Как и ранее, приближенное решение ищем в виде разложения (3.20) в ряд по пробным функциям, удовлетворяющим следующим требованиям:

1. k C1a,b , k 0,1,2,

2.Функции k линейно независимы на [a, b] .

3.Функция 0 удовлетворяет граничным условиям (3.19),

1 0 a 2 0 a A,1 0 b 2 0 b B;

остальные функции этой системы - однородным граничным условиям

Подставим выражение (3.20) в функционал (3.38):

b

yn p x yn 2 q x yn2 2f x yn dx

a

Обозначим:

b

C0 p 02 q 20 2f 0 dx ,

a

b

fk p 0 k q 0 k f k dx ,

a

b

Cjk p k j q k j dx . a

75

Теперь последнее выражение можно записать в виде:

yn C0 2 fk ak Ckjakaj .

откуда получаем систему линейных алгебраических уравнений относительно коэффициентов разложения (3.20) искомого решения в ряд по пробным функциям:

Условия существования и единственности решения этой системы алгебраических уравнений устанавливаются следующей теоремой:

Теорема 3.5. Пусть коэффициенты дифференциального уравнения (3.22) удовлетворяют условиям:

Тогда система алгебраических уравнений метода Ритца имеет единственное решение.

Доказательство этой теоремы проводится аналогично доказательству теоремы 3.2.

Сходимость метода Ритца

Пусть y x доставляет минимум функционалу (3.38), и имеет место

lim yk y

k

3) последовательность функций yk x является минимизирующей.

15 Такая последовательность функций называется минимизирующей.

76