
Boyarshinov_ChM_T1
.pdfМИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РОССИЙСКОЙ
ФЕДЕРАЦИИ
ПЕРМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
КАФЕДРА МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ СИСТЕМ И ПРОЦЕССОВ
М. Г. БОЯРШИНОВ
Ч И С Л Е Н Н Ы Е М Е Т О Д Ы
Учебное пособие для студентов направления
“ПРИКЛАДНАЯ МАТЕМАТИКА И ИНФОРМАТИКА”
Часть 1
ПЕРМЬ
УДК 681.3 Б 86
Численные методы: Учебное пособие для студентов направления “Прикладная математика и информатика” / М. Г. Бояршинов; Перм. гос. техн. ун-т. Пермь, . - 176 с.
Учебное пособие написано на основе курса, читаемого студентам направления “Прикладная математика и информатика” (специализация “Математическое моделирование”) в Пермском государственном техническом университете.
Введены основные понятия математического моделирования, рассмотрены причины и источники погрешностей при проведении вычислительного эксперимента. Рассмотрены прямые и итерационные методы решения систем линейных и нелинейных алгебраических уравнений, вопросы аппроксимации функций полиномами и сплайнами, вопросы численного дифференцирования и интегрирования. Сформулирована алгебраическая проблема собственных значений и векторов, определены пути ее решения. Основное внимание уделяется оценкам погрешности при проведении вычислений, устойчивости и сходимости алгоритмов решения прикладных задач.
Пособие предназначено для студентов и аспирантов вузов, специалистов, занимающихся вопросами построения моделей систем и процессов. Может быть полезно учителям средних учебных заведений при проведении факультативных занятий по компьютерному моделированию.
Печатается по решению редакционно - издательского совета Пермского государственного технического университета.
Табл. 13. Ил. 28. Библиогр. : 12 назв.
Рецензенты:
д-р физ.-мат наук Е. Л. Тарунин; зав. кафедрой математики и информатики Перм. гос.
ун-та,
канд. физ.-мат. наук О. Ю. Сметанников
ISBN 5 - 88151 - 158 - 1 |
Пермский государственный |
|
технический университет, 1998 |
2
О Г Л А В Л Е Н И Е |
|
Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
6 |
1. Источники и причины погрешностей математической модели. . . . . . . . . . . . . . . . . |
8 |
Погрешность математической модели. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
10 |
Погрешность исходных данных. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
11 |
Погрешность численного метода. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
11 |
Погрешность проведения расчетов на вычислительных машинах. . . . . . . . . . . |
13 |
Погрешности округления чисел в ЭВМ. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
13 |
Погрешность результатов вычисления арифметических операций . . . . . . . . . |
14 |
“Потеря порядка” и “переполнение” при проведении вычислений на ЭВМ |
15 |
Машинная реализация вычислений. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
16 |
Контрольные вопросы и задания. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
16 |
2. Системы линейных алгебраических уравнений. . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
17 |
Прямые методы решения. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
17 |
Метод Гаусса. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
18 |
Определение числа операций алгоритма метода Гаусса. . . . . . . . . . . . . . . . . |
27 |
Вычисление определителя матрицы. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
28 |
Построение обратной матрицы. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
29 |
Метод квадратного корня. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
30 |
Определение числа операций алгоритма метода квадратного корня. . . . . . . |
35 |
Устойчивость системы линейных алгебраических уравнений. . . . . . . . . . . . . . . |
36 |
Итерационные методы решения. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
42 |
Метод Якоби. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
42 |
Метод Зейделя. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
45 |
Сходимость итерационных методов. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
47 |
Скорость сходимости. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
54 |
Полиномы Чебышёва. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
55 |
Итерационный метод с чебышёвским набором параметров. . . . . . . . . . . . . . |
61 |
Неявный метод с чебышевским набором параметров. . . . . . . . . . . . . . . . . . . |
65 |
Метод минимальных невязок. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
66 |
Метод минимальных поправок. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
67 |
Метод скорейшего спуска. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
69 |
3
Неявный метод скорейшего спуска. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
70 |
Контрольные вопросы и задания. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
71 |
3.Нелинейные уравнения. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
73 |
Методы вычисления корней нелинейного уравнения. . . . . . . . . . . . . . . . . . . . . . |
73 |
Метод половинного деления. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
73 |
Метод простых итераций. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
75 |
Метод Ньютона. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
80 |
Модификации метода Ньютона. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
84 |
Системы нелинейных уравнений. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
87 |
Метод простых итераций. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
87 |
Метод релаксации. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
88 |
Метод Ньютона. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
89 |
Нелинейный вариант метода Якоби. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
90 |
Нелинейный вариант метода Зейделя. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
91 |
Контрольные вопросы и задания. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
93 |
4. Аппроксимация функций. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
94 |
Интерполяция степенными функциями. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
95 |
Интерполяционный многочлен Ньютона. . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
95 |
Интерполяционная формула Лагранжа. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
99 |
Погрешность полинома Ньютона (Лагранжа) . . . . . . . . . . . . . . . . . . . . . . . . |
99 |
Сходимость интерполяционного процесса. . . . . . . . . . . . . . . . . . . . . . . . . . . |
101 |
Интерполяционный многочлен Эрмита. . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
103 |
Интерполяция сплайнами. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
106 |
Построение кубического сплайна. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
106 |
Сходимость процесса интерполяции кубическими сплайнами. . . . . . . . . . . |
110 |
Наилучшее приближение в гильбертовом пространстве. . . . . . . . . . . . . . . . |
117 |
Метод наименьших квадратов. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
122 |
Контрольные вопросы и задания. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
125 |
5. Алгебраическая проблема собственных значений. . . . . . . . . . . . . . . . . . . . . . . . . . |
126 |
Устойчивость собственных значений и векторов. . . . . . . . . . . . . . . . . . . . . . . . |
128 |
Определение собственных значений и векторов. . . . . . . . . . . . . . . . . . . . . . . . . |
132 |
Метод интерполяции. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
132 |
Трехдиагональные матрицы. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
133 |
4
Поиск собственных векторов. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
135 |
Частичная проблема собственных значений. . . . . . . . . . . . . . . . . . . . . . . . . . . . |
138 |
Метод линеаризации. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
138 |
Степенной метод. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
140 |
Метод обратных итераций. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
141 |
Контрольные вопросы и задания. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
144 |
6.Численное дифференцирование. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
145 |
Конечно-разностная аппроксимация. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
145 |
Применение интерполяционных формул. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
147 |
Контрольные вопросы и задания. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
148 |
7.Численное интегрирование. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
149 |
Формула прямоугольников. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
150 |
Формула трапеций. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
153 |
Формула Симпсона. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
156 |
Формула Эйлера. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
160 |
Оценка погрешности методом Рунге. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
161 |
Квадратурные формулы интерполяционного типа. . . . . . . . . . . . . . . . . . . . . . . |
163 |
Квадратурные формулы наивысшей точности. Формулы Гаусса. . . . . . . . . . . |
164 |
Контрольные вопросы и задания. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
172 |
Предметный указатель. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
173 |
Библиографический список. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
176 |
5
В В Е Д Е Н И Е
. . . Лист раскаленного металла с огромной скоростью движется по рольгангу прокатного стана. Что произойдет, если на его пути встретится препятствие?
. . . Произошел внезапный выброс в атмосферу ядовитого газа. Как поведет себя опасное облако при сильном северном ветре? А при среднем восточном или слабом южном?
А если в это же время пойдет дождь или снег?
. . . Строить ли мощную тепловую электростанцию возле города? На севере или востоке от жилых районов? Или полностью отказаться от строительства, чтобы не вызвать экологическую катастрофу?
Огромное количество вопросов возникает в процессе человеческой деятельности,
ответы на которые получить чрезвычайно трудно, а порой просто невозможно с помощью натурных исследований, которые могут стоить огромных денег или быть связанными с угрозой жизни людей. А как быть с объектами, недоступными для исследования,
расположенными в недрах Земли или в далеком космосе? Какие процессы происходят,
например, в глубине Солнца или планет солнечной системы? Как ведет себя материал заготовки при его термической и механической обработке? Посмотреть, “потрогать руками” то, что происходит в раскаленном добела слитке металла при прокатке на стане металлургического производства просто невозможно!
Здесь специалисту приходит на помощь особая форма изучения окружающей действительности - математическое моделирование, то есть моделирование посредством математических символов и операций над ними. Вполне понятно, что для квалифицированного проведения исследовательской работы требуется знать многие разделы математики: математический и функциональный анализ, теорию обыкновенных дифференциальных уравнений и уравнений математической физики, тензорный анализ и дифференциальную геометрию, теорию вероятности и интервальный анализ.
В то же время специалист в области математического моделирования должен владеть основами таких дисциплин, как механика сплошных сред, физические основы неупругости и прочности металлов и сплавов, теорию определяющих соотношений, физику и механику жидкостей, газов, полимеров.
Основным инструментом исследователя-математика является электронно-
вычислительная машина, владеть которой он обязан в совершенстве. Для этого профессионал в области математического моделирования должен в полной мере постичь тонкости программирования на алгоритмических языках высоко уровня, знать современные технологии разработки и создания программных продуктов, владеть навыками графического отображения числовой информации.
6
Рассматриваемые в фундаментальных, прикладных и инженерных дисциплинах вопросы совершенно органично соединяются и переплетаются при изучении численных методов решения прикладных инженерных задач. Курс “Численные методы”, читаемый студентам направления “Прикладная математика и информатика” Пермского государственного технического университета, является в некотором смысле синтетическим,
переводящим приобретенные ранее знания в новое качество. Успешное освоение этого курса дает исследователю чрезвычайно мощный инструмент получения принципиально новых знаний об окружающем мире посредством компьютерного моделирования.
Большую помощь при подготовке настоящего пособия оказали студенты специальности “Математическое моделирование” разных курсов, внимательно и заинтересованно слушая лекция, делая интересные и неожиданные замечания, читая рукопись и высказывая конструктивные предложения по совершенствованию курса,
принимая непосредственное участие в реализации алгоритмов решения задач на вычислительных машинах.
За оказанную помощь хочется особо поблагодарить Дмитрия Киселева (гр. ММ-90),
Алексея Козлинских и Алексея Харченко (гр. ММ-92), Андрея Черепанова и Романа Новокшанова (гр. ММ-93), Михаила Басина, Николая Чепурных и Сергея Селезнева (гр.
ММ-94).
7

1 . И С Т О Ч Н И К И И П Р И Ч И Н Ы
ПО Г Р Е Ш Н О С Т Е Й М А Т Е М А Т И Ч Е С К О Й
МО Д Е Л И
Стермином “компьютерное моделирование” непосредственно связано введенное академиком А.А. Самарским1 понятие о вычислительном эксперименте [1], то есть технологии исследования сложных проблем, основанной на построении и анализе с помощью электронной вычислительной машины математических моделей изучаемого объекта.
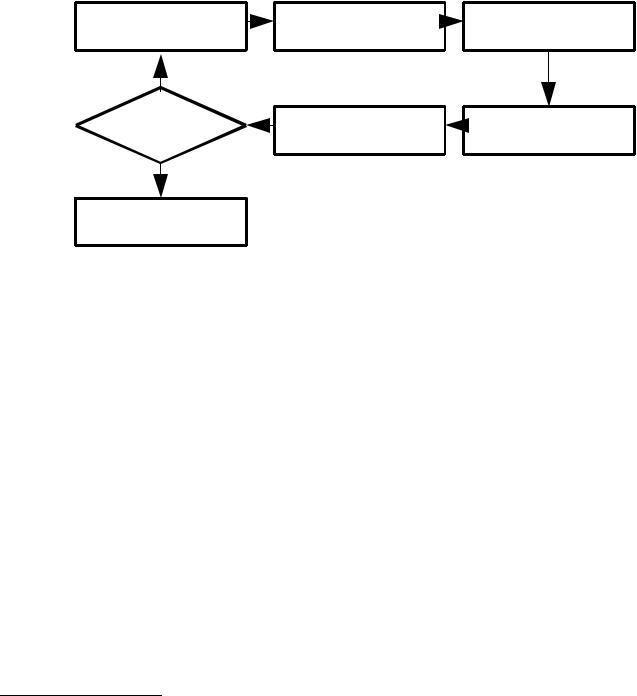
Под объектом исследования (рис. 1.1) будем понимать как материальные тела (жидкие,
абсолютно твердые, деформируемые, газообразные), так и технологические процессы и физические явления. Из всего многообразия свойств, присущих объекту исследования,
выделяются и рассматриваются только те, что представляют интерес в данной конкретной ситуации. Так, например, при анализе процесса обработки металла давлением, как правило,
пренебрегают его магнитными и электрическими свойствами, не учитывают химические реакции и так далее. На начальном этапе определяются законы, описывающие лишь интересующее исследователя поведение объекта. Например, при моделировании движения космического аппарата вне атмосферы Земли достаточно использовать уравнения классической механики и не учитывать его прочностные характеристики; при исследовании химических превращений вещества нет смысла учитывать упругие или пластические характеристики материала.
Следующий этап - математическая модель - представляет собой формализованную запись выбранных законов, описывающих поведение объекта, посредством символов и операций над ними. В общем случае математическая модель включает запись систем уравнений (алгебраических, обыкновенных дифференциальных или в частных производных,
интегральных, интегро-дифференциальных), неравенств, начальных и граничных условий.
1 |
Самарский Александр Андреевич [19.2.1919] окончил в 1945 году Московский государственный |
|
|
|
университет. С 1959 года - профессор МГУ. В 1966 году был избран членом-корреспондентом, а в 1976 - |
|
действительным членом АН СССР. С 1984 года является почетным доктором Технического университета |
|
города Карл-Маркс-Штадт. Награжден орденами Трудового Красного Знамени (1969), Октябрьской |
|
Революции (1975), Ленина (1954, 1956, 1979), Герой Социалистического Труда (1979), лауреат Ленинской |
|
премии (1962). |
Здесь и далее биографические сведения соответствуют тексту книги “Математический энциклопедический словарь”. -М.: Советская Энциклопедия, 1988. - 847 с.
8
В случае, если для записанной системы уравнений невозможно получить точное2
решение, используются соответствующие методы приближенного3 или численного4 решения с использованием вычислительной техники.
Объект |
Математическая |
Численный |
исследования |
модель |
метод |
Нет |
|
|
Адекватность? |
Расчеты и анализ |
Программирование |
|
результатов |
для ЭВМ |
Да |
|
|
Эксплуатация |
|
|
программы |
|
|
Рис 1.1. Схема выполнения вычислительного эксперимента.
Программирование для электронных вычислительных машин представляет собой процесс подготовки кода, реализующего вычислительные алгоритмы численного решения задач на языках высокого уровня. Существуют специальные способы и подходы, технологии создания программных продуктов, гарантирующие подготовку компьютерных программ в заданные сроки с высоким качеством. К их числу относятся технологии структурного и объектно-ориентированного программирования.
Проведение расчетов и анализ результатов - этап, требующий значительных интеллектуальных усилий и навыков по обработке, представлению и осмыслению получаемых решений. Необходима интерпретация громадных объемов числовой информации в виде графиков, таблиц, изолиний и так далее. Основная цель этого этапа -
установление степени адекватности численных результатов компьютерного моделирования данным натурных наблюдений и измерений.
2Точным называется решение, полученное в элементарных функциях.
3Под приближенным понимается решение, получаемое в виде последовательности некоторых приближений
(например, ряды Фурье, Тейлора и так далее).
4 |
Численное решение предполагает получение таблицы значений искомой функции для конечного числа |
|
узловых значений аргументов (методы конечных и граничных элементов, сеточные и ряд других). |
9
В случае, если имеется существенное отклонение расчетных и экспериментальных данных, необходимо вернуться к исходному и промежуточным этапам построения математической модели с целью уточнения законов, описывающих поведение объекта,
выбора более приемлемого метода решения математической задачи, проверки правильности машинного кода программы. При получении достаточной степени точности получаемых численных результатов переходят к “промышленной” эксплуатации компьютерной модели.
Следует четко понимать, что целью математического моделирования является не только (и даже не столько!) описание существующих явлений в поведении объекта, сколько предсказание его поведения в нестандартных ситуациях. Одно из основных направлений использования компьютерного моделирования - поиск оптимальных вариантов внешнего воздействия на объект с целью получения наивысших показателей его функционирования:
минимальная себестоимость, максимальная производительность, наибольшая прибыль,
наименьшие затраты и потери и так далее.
Погрешность математической модели
Точность математической модели определяется степенью правильности принятых гипотез и упрощений, описывающих исследуемый объект. Оценка точности в этом случае может производиться только проверкой степени выполнения принятых гипотез при натурном наблюдении. Так, например, для моделирования поведения металла в процессах пластического деформирования, как правило, используют модели вязкой жидкости. Однако такое предположение может быть использовано лишь в процессах, проводящихся при достаточно высоких температурах.
Понятно, что погрешности этого рода являются неустранимыми в рамках принятых допущений и предположений. Повышение точности модели возможно при уточнении гипотез и законов, описывающих поведение исследуемого объекта: увеличение степеней свободы механизмов, повышение размерности задачи, отказ от грубых допущений. Это, как правило, приводит к повышению сложности систем уравнений и алгоритмов решения поставленной задачи.
Погрешность исходных данных
Любая математическая модель использует для проведения расчетов некоторые данные, получаемые с помощью натурных измерений. В силу погрешности измерительных инструментов, ошибок при снятии размеров, нестабильности свойств и размеров тел практичеси все исходные данные содержат погрешности, влияющие в большей или меньшей степени на результаты расчетов. Точность определения параметров в промышленных условиях, как правило, составляет 1 - 10 % . Точные иследования при наличии достаточной инструментальной базы и специальных условий позволяют достичь 0,001 - 0,0001%
10
