
Boyarshinov_ChM_T1
.pdf
ck 1hk 1 ckhk 23 ck 1 |
ck hk 1 31 ck ck 1 hk |
||||||
f xk 1 f |
xk |
f xk f |
xk 1 |
|
k 1,n 1. |
||
2 |
hk 1 |
|
|
hk |
|
, |
|
|
|
|
|
|
|
||
Приводя подобные слагаемые и учитывая условия (4.14) и (4.15), получаем
ck 1hk 2ck hk hk 1 ck 1hk 1
|
f xk 1 f xk |
f xk f xk 1 |
|
|
|
|
|
k 1,n 1, |
(4.17) |
||||
6 |
hk 1 |
|
, |
|||
|
|
hk |
|
|
|
|
|
|
|
|
|
|
|
|
0, |
cn 0. |
|
|
|
|
c0 |
|
|
|
|
||
В итоге всех преобразований получена система линейных алгебраических уравнений с трехдиагональной матрицей коэффициентов. После определения всех неизвестных величин ck , k 0,n определяются остальные коэффициенты сплайнов
|
|
c |
k |
c |
k 1 , |
|
|
|
|
|
dk |
|
hk |
|
|
|
|
||||
|
|
fk , |
|
|
|
|
|
|||
ak |
|
|
|
|
|
|
|
|||
b |
ck |
h |
k |
dk h2 |
fk |
fk 1 , |
k 1,n . |
|||
|
k |
2 |
|
6 |
k |
|
hk |
|
||
|
|
|
|
|
|
|
||||
Сходимость процесса интерполяции кубическими сплайнами
Покажем, что при неограниченном увеличении числа n узлов на отрезке [a,b]
последовательность сплайн-функций сходится к интерполируемой функции.
Для упрощения рассмотрим последовательность сеток с равномерными
расположениями узлов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n xi |
a h i, |
i 0,n , |
h b a . |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
В этом случае система уравнений (4.17) принимает более простой вид |
||||||||||||||||
c |
4c |
k |
c |
|
6 |
|
f x |
|
2f x |
k |
f x |
|
, |
k 1,n 1, |
||
|
k 1 |
|
k 1 |
h |
2 |
|
k 1 |
|
|
|
k 1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cn 0. |
|
|
|
|
|
|
|
|
|
|
|
|
||
c0 0, |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пусть аппроксимируемая функция f(x) непрерывна вместе со своими производными вплоть до четвертого порядка, то есть f C(4) a,b , а также имеют место равенства
f (a) 0, |
f (b) 0. |
Обозначим:
109

g a,b |
maxg(x) |
|
|
|
|
|
x a,b |
|
|
max (xk ) |
|
Wn |
xk Wn |
|
1
fxx,k h2 f xk 1 2f xk f xk 1
M4  fIV
fIV [a,b] .
[a,b] .
-чебышевская норма на отрезке [a,b];
-чебышевская норма на сеточной области n ;
-разностный аналог второй производной аппроксимируемой функции f(x);
Теперь система уравнений (4.17) выглядит следующим образом: |
|||||
|
|
|
ck 1 6fxx,k , |
k 1,n 1, |
|
ck 1 4ck |
|||||
|
|
|
|
|
(4.18) |
c |
0 |
0, c |
n |
0. |
|
|
|
|
|
||
Лемма 4.1. Для всех f(x) C(4) a,b справедлива оценка |
f S |
3M |
4h2. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n 4 |
|
Доказательство. В силу определения введенной нормы на сеточной области |
||||||||||||||
необходимо проверить точки xk , для которых S xk ck . |
|
|
|
|||||||||||
Обозначим погрешность |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
k |
c |
k |
|
x |
k |
k 0,n |
. |
|
|
|
||
|
|
|
f |
|
, |
|
|
|
|
|||||
Для k = 0 и k = n, в частности, z0 zn |
0. |
|
|
|
|
|
||||||||
Уравнения (4.18) в новых обозначениях принимают вид |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
4f xk f xk 1 , |
k 1,n 1, |
||||
zk 1 4zk zk 1 6fxx,k f xk 1 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.19) |
|
0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
z0 0, zn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обозначим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
6fxx,k f xk 1 4f xk f xk 1 |
|
(4.20) |
|||||||||||
6 fxx,k f xk f xk 1 4f xk f xk 1 6f xk
6 fxx,k f xk f xk 1 2f xk f xk 1 6 fxx,k f xk f xx,k h2 ,
причем
f xx,k |
|
f xk 1 2f xk f xk 1 |
h2 |
- разностный аналог второй производной функции f x в точке xk 1 .
Воспользуемся формулами Тейлора:
110

f |
|
x |
k 1 |
|
f |
|
x |
k |
|
|
|
|
|
x |
k |
|
h2 |
|
x |
k |
|
h3 |
|
x |
k |
|
h4 |
k |
|
|
|
|
|
|
|
x |
k |
,x |
k 1 |
|
, |
||||||||||||||||||||
|
|
|
|
|
2 |
6 |
24 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
hf |
|
|
|
|
f |
|
|
|
|
f |
|
|
|
|
|
fiv |
|
|
, |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
f |
|
x |
k 1 |
|
f |
|
x |
k |
|
|
|
|
|
x |
k |
|
h2 |
|
x |
k |
|
h3 |
|
x |
k |
|
h4 |
k |
|
|
|
|
|
|
x |
k 1 |
,x |
k |
|
. |
|||||||||||||||||||||
|
|
|
|
|
2 |
6 |
24 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
hf |
|
|
|
|
f |
|
|
|
|
f |
|
|
|
|
fiv |
|
|
, |
|
|
|
|
|
||||||||||||||||||||||||||||||||
Аналогичным образом построим разложение для функции f (x): |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
x |
k |
|
|
|
|
|
|
k |
h2 |
|
|
|
|
|
|
x |
k |
,x |
k 1 |
|
, |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
f x |
|
|
f |
|
|
hf x |
|
|
|
|
fiv |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
x |
k |
|
|
|
|
x |
k |
h2 |
k |
|
|
|
|
|
|
|
x |
k 1 |
,x |
k |
|
. |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
f x |
|
|
f |
|
|
|
hf |
|
|
|
|
|
|
fiv |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Теперь можно оценить разностные аппроксимации производных: |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
h |
4 |
|
|
h |
4 |
fiv |
|
|
|
|
|
|
|
h |
2 |
|
fiv fiv , |
|
|||||||||||||||||||||||||||||
|
f |
|
|
|
|
|
|
|
|
|
|
|
fiv |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
xx,k |
h2f x |
k |
|
|
|
|
f x |
k |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
h |
2 |
|
|
|
|
|
|
|
|
24 |
|
k |
|
|
|
24 |
|
k |
|
|
|
|
|
|
|
24 |
k |
|
|
|
|
|
k |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
f |
|
|
|
|
1 |
|
|
|
|
2 |
fiv h |
2 |
|
|
|
1 |
|
fiv fiv . |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
xx,k |
|
h |
|
|
|
fiv |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
2 |
|
|
2 |
|
k |
|
|
|
|
2 |
|
k |
|
|
2 |
|
k |
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Подставим полученные выражения в формулы (4.20):
 k
k 
 6 fxx,k f xk f xx,k h2
6 fxx,k f xk f xx,k h2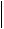 6fxx,i f xk
6fxx,i f xk 
 f xx,k h2
f xx,k h2
|
|
|
|
1 |
|
|
2 |
iv |
|
|
1 |
2 |
|
|
iv |
|
1 |
2 |
|
iv |
|
1 |
|
2 |
iv |
. |
|
|
|
|
|
|
|||||
|
|
|
|
4h |
|
|
fk |
4h |
|
|
fk |
2h |
|
fk |
2h |
|
fk |
|
|
|
|
|
|
|
|||||||||||||
Отсюда получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
max |
k |
h2 |
maxfiv |
|
|
|
maxfiv |
|
2maxfiv |
|
|
2maxfiv |
|
|
|
|
||||||||||||||||||||
Wn |
x |
W |
n |
|
|
|
|
4 |
|
W |
k |
|
|
|
W |
n |
k |
|
W |
n |
k |
|
W |
k |
|
|
|
||||||||||
|
k |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
||||
6h2 |
f |
|
3M |
4 |
h2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4 |
Wn |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Теперь, согласно формулам (4.19), получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
4zk k zk 1 zk 1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
4zk |
k zk 1 |
zk 1 |
max k maxzk 1 |
max zk 1 |
|
n |
2 z |
|
n |
. |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
xk n |
|
|
xk n |
|
|
|
xk n |
|
|
|
|
|
|
|
|
|
|
||||||||
Поскольку эта оценка имеет место во всех точках сеточной области |
|
n , то она |
|||||||||||||||||||||||||||||||||||
справедлива и в точке, где |
|
|
zk |
|
достигает максимума, то есть |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
 zk
zk 
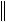 zk
zk 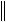 n .
n .
Следовательно,
4 z
z n
n 
 n 2
n 2 z
z n ,
n ,
111

|
|
|
|
|
z 1 |
3M4h2 , |
|
|
|
|||||
|
|
|
|
|
n |
2 |
n |
4 |
|
|
|
|
|
|
откуда сразу следует утверждение леммы 4.1. |
|
|
|
|
|
|
||||||||
Теорема 4.3. Для любой функции |
f C(4) a,b |
справедливы оценки: |
|
|||||||||||
|
|
|
|
|
f S a,b |
M4h4 |
, |
|
|
|
(4.21) |
|||
|
|
|
|
|
f S a,b M4h3 , |
|
|
|
(4.22) |
|||||
|
|
|
|
|
f S a,b |
M4h2 . |
|
|
|
(4.23) |
||||
Доказательство. Рассмотрим |
произвольный |
отрезок xk 1,xk , k 1,n. Согласно |
||||||||||||
определению сплайна (4.8), а также учитывая формулы (4.11), получаем |
|
|
||||||||||||
|
|
c |
c |
x xk |
|
x xk 1 |
|
xk x |
1 ck 1, |
|||||
Sk x ck dk x xk ck |
k h |
k 1 |
ck |
h |
ck 1 |
h |
ck |
|||||||
|
|
|
|
|
a x xk , |
0 a 1. |
|
|
|
|
||||
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
Несложно проверить справедливость следующего тождества: |
|
|
||||||||||||
f x S x |
|
f xk ck 1 f xk 1 |
ck 1 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.24) |
|
|
|
f x f xk |
1 f x f xk 1 |
. |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Оценим первое слагаемое в правой части (4.24) :
 f xk ck 1 f xk 1 ck 1
f xk ck 1 f xk 1 ck 1 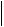
 f xk ck
f xk ck  1
1  f xk 1 ck 1
f xk 1 ck 1
|
|
|
|
|
|
|
|
|
|
|
x |
k |
c |
k |
|
|
|
maxf |
|
x |
|
c |
k 1 |
|
|
|
|
|
|
|
|
|||||
|
|
|
maxf |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
xk Wn |
|
|
|
|
|
|
|
|
|
xk Wn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
f S |
|
1 |
|
f S |
3M |
|
h2 . |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
k |
Wn |
|
|
|
|
|
k 1 Wn |
|
|
4 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|||
Проведем оценку второго слагаемого. Согласно формуле Тейлора |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
f xk f x xk |
x f x xk |
x 2 |
fiv k , |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
x 2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
f |
x |
k 1 |
f |
x |
|
|
|
x |
|
x f x |
|
|
|
|
, |
|
|
|
, |
|
|
x |
|
,x |
k |
. |
||||||||||
k 1 |
|
|
k 1 |
|
fiv |
|
|
|
k |
k |
k 1 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
k |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда получаем соотношения для разностей |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
f x f xk x xk f x xk |
x 2 |
fiv k , |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
112

f x f xk 1 x xk 1 f x xk 1 x 2 fiv k . 2
Теперь можно преобразовать второе слагаемое в правой части формулы (4.24):
f x f xk 1 f x f xk 1
|
x |
|
x 2 |
|
|
x |
|
|
x 2 |
|
x xk f x |
|
k |
2 |
fiv k 1 x xk 1 f x |
|
k 1 |
|
fiv k |
||
|
|
|
|
|
|
|
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
f x x xk 1 x xk 1 12 x xk 2 fiv k 1 x xk 1 2fiv k
f x 1 h 1 h 12 h2 1 2 fiv k 1 2h2fiv k
1 h2 1 1 fiv k fiv k .
2
Произведем оценку:
 f x f xk 1 f x fk 1
f x f xk 1 f x fk 1 
|
1 h2 1 1 fiv |
|
k |
|
fiv |
k |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
max |
|
|
fiv |
|
|
max |
|
|
|
|
|
|||||||||||||||||
1 h2 |
1 |
|
|
1 |
|
k |
|
|
k |
fiv |
|
||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
k 1 |
,x |
|
|
|
|
|
|
|
|
|
k 1 |
,x |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
M4 h2 1 M4 h2 . |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
При выводе последнего соотношения учтено, что |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
max |
fiv |
|
x |
|
max fiv |
|
x |
|
M |
4 |
, |
a 1 a |
|
|
1 |
|
|
||||||||||||||||
x x |
k 1 |
,x |
k |
|
|
x a,b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|||
Теперь можно оценить левую часть тождества (4.24):
f x Sk x 3M4h2 |
M4h2 |
7M4h2 |
M4h2, |
x xk 1,xk . (4.25) |
4 |
8 |
8 |
|
|
Учитывая, что выражение (4.25) справедливо для любого отрезка, его можно использовать и для оценки погрешности 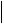 f x S x
f x S x  на всем участке a,b :
на всем участке a,b :
 f x S x
f x S x 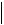 M4h2 .
M4h2 .
Отсюда получаем
f S a,b max f x S x M4h2 ,
x a,b
то есть утверждение (4.23) теоремы.
113

Для доказательства соотношения (4.22) введем на отрезке xk 1,xk вспомогательную функцию r x f x Sk x . В силу определения сплайна, r xk 1 r xk 0. Но тогда, в
соответствии с теоремой Ролля29, существует хотя бы одна точка xk 1,xk , r 0.
В этом случае, используя теорему Лагранжа, можно произвести оценку
 r x
r x 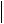
 r x r
r x r 
 r x
r x 
 r
r  h ,
h ,
откуда, с учетом соотношения (4.25), получаем
 f x Sk x
f x Sk x 
 f Sk
f Sk  h M4h3 .
h M4h3 .
Поскольку это неравенство справедливо на любом отрезке xk 1,xk , с его помощью можно получить получить утверждение (4.22) теоремы:
f S a,b max f x Sk x M4h3 .
x a,b
Для получения последнего утверждения (4.21) построим на отрезке xk 1,xk функцию
g t f t Sk t K t xk 1 t xk .
Из условия обращения этой функции в нуль для произвольно выбранного значения x xk 1,xk
g x f x Sk x K x xk 1 x xk 0
определим значение константы
f x Sk x K x xk 1 x xk .
Очевидно, что теперь
g x g xk g xk 1 0.
Это означает, что существует хотя бы одна точка xk 1,xk , g 0. Отсюда получаем
g f Sk 2K 0,
f Sk 2K 2 f x Sk x ,
x xk 1 x xk
29 Ролль Мишель [21.4.1652 - 8.11.1719] - французский математик. С 1685 года является членом Парижской
академии наук.
Теорема Ролля, [10]: если функция f(x) непрерывна в замкнутом интервале a,b , дифференцируема во всех его
внутренних точках и имеет на концах интервала равные значения, то существует хотя бы одна точка
a,b , f 0.
114
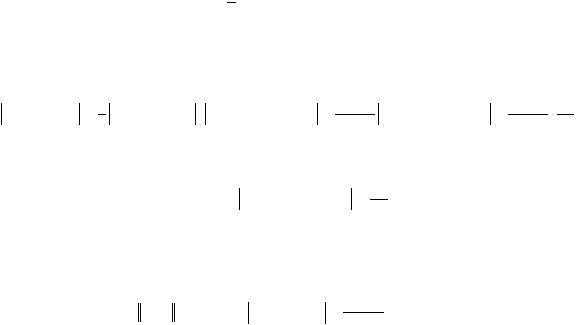
f x Sk x 12 f Sk x xk 1 x xk .
Отсюда, с использованием неравенства (4.25), следует оценка отклонения значения сплайн-аппроксимации от значения функции для выбранной точки x xk 1,xk :
f x Sk x 1 f Sk x xk 1 x xk M4h2 |
x xk 1 |
x xk M4h2 h2 . |
|||||||||
2 |
|
|
|
|
|
|
|
2 |
|
2 |
4 |
Здесь учтено, что |
|
|
|
|
|
|
|
|
|
|
|
x x ,x |
|
|
k 1 |
|
|
k |
h2 |
|
|
||
x x |
x x |
. |
|
|
|||||||
max |
k |
|
|
|
|
|
|||||
|
k 1 |
|
|
|
|
|
|
4 |
|
|
|
Поскольку последнее неравенство справедливо для любого x xk 1,xk , получим
выражение (4.21) теоремы:
f S a,b max f x Sk x M84h4 M4h4 ,
x a,b
что и требовалось доказать.
115

Наилучшее приближение в гильбертовом пространстве
Рассмотрим линейное нормированное пространство H, в котором задана конечная система линейно-независимых элементов k H, k 0,n . Требуется заменить некоторый элемент f H линейной комбинацией
|
|
n |
|
|
j c0j0 |
c1j1 cnjn |
ckjk , |
(4.26) |
|
|
|
k 0 |
|
|
где j - обобщенный многочлен. |
|
|
|
|
Задача о наилучшем приближении заключается в поиске среди множества линейных |
||||
|
|
|
n |
|
комбинаций вида (4.26) такой, для которой отклонение |
f ckjk |
было бы наименьшим. |
||
|
|
|
k 0 |
|
|
~ |
n |
|
|
Такой элемент (обобщенный |
~ |
является |
элементом наилучшего |
|
полином) j |
ckjk |
|||
k 0
приближения.
Пусть H - гильбертово пространство с нормой, порожденной скалярным произведением
b
f,g H f x g x dx,
|
a |
|
|
|
f |
f,f 1 2 |
b |
f2 |
1 2 |
|
(x)dx . |
|||
H |
H |
|
|
|
|
|
a |
|
|
Рассмотрим отклонение приближения (4.26) от элемента f :
f H2 |
|
n |
|
|
|
n |
|
|
|
|
|
|
|
|
||
f ck k ,f cp |
p |
|
|
|
|
|
|
|||||||||
|
|
|
k 0 |
|
|
|
p 0 |
|
H |
|
|
|
|
|
|
|
f,f H |
|
n |
|
|
|
|
n |
|
|
|
|
n |
n |
|
|
|
f, cp p |
|
|
|
ck k |
,f |
|
|
ck k, cp p |
|
|
(4.27) |
|||||
|
|
p 0 |
|
|
H |
k 0 |
|
|
H |
k 0 |
p 0 |
|
H |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
n |
|
|
|
|
|
n n |
|
|
|
|
|
|
|
|
f H2 2 ck f, k H ckcp k, p H |
|
|
|
||||||||||||
|
|
|
k 0 |
|
|
|
k 0 p 0 |
|
|
|
|
|
|
|||
Введем обозначения:
A - матрица с компонентами akp jk,jp H, k,p 0,n ;
c - вектор коэффициентов c0,c1, ,cn T ;
f - вектор f0,f1, , fn T, fk f,jk H, k 0,n .
Скалярное произведение векторов определим обычным образом:
117

n |
|
|
u,v ukvk , |
u,v Rn 1 . |
|
k 0 |
|
|
Теперь выражение (4.27) можно представить следующим образом: |
|
|
f j 2H Ac,c 2 f,c f 2H . |
(4.28) |
|
Очевидно, что поиск элемента ~ наилучшего приближения сводится теперь к j H
поиску минимума функционала
|
|
|
|
|
|
|
|
|
F(c) Ac,c 2 f,c , |
|
|
(4.29) |
||||||
поскольку слагаемое f 2H |
|
в выражении (4.28) от параметров ck , |
k 0,n не зависит. |
|
||||||||||||||
|
|
Исследуем |
свойства |
матрицы |
A. |
Поскольку |
akp jk,jp H |
jp,jk H apk , |
то |
|||||||||
очевидно, что матрица A симметрична. |
|
|
|
|
|
|
|
|
||||||||||
|
|
Если положить f = 0, |
то из соотношения (4.28) можно получить: |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
Ac,c j 2 0 |
c Rn 1 . |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
|
|
|
|
|
|
|
Если для какого-либо c Rn 1 |
имеет место равенство Ac ,c 0, то в силу j 2H |
0 |
||||||||||||||
получаем, |
что |
j c j |
0 |
cj |
1 |
c j |
n |
0, и |
из |
условия |
линейной |
независимости |
||||||
|
|
|
|
0 |
|
1 |
|
n |
|
|
|
|
|
|
|
|||
|
k |
H, k 0,n |
следует |
: |
|
c |
0, |
c 0, |
, |
c 0. |
Но |
это |
означает, |
что |
||||
|
|
|
|
|
|
|
|
0 |
|
1 |
|
n |
|
|
|
|
||
Ac,c 0 |
c 0, то есть матрица А является положительно определенной. |
|
|
|||||||||||||||
|
|
Теорема 4.4. Если А - симметричная положительно определенная матрица, |
f - |
|||||||||||||||
заданный вектор, |
то функционал (4.29) |
имеет единственную точку минимума ~c тогда и |
||||||||||||||||
только тогда, когда вектор ~c удовлетворяет системе линейных алгебраических уравнений
~ |
|
(4.30) |
Ac |
f . |
Доказательство. В силу положительной определенности матрица А имеет определитель, отличный от нуля, то есть система уравнений (4.30) разрешима и имеет
единственное решение. |
|
|
|
|
|
Достаточность теоремы. Пусть ~c |
является решением системы уравнений (4.30). Для |
||||
произвольного вектора v, согласно определению (4.29), |
имеет место: |
||||
~ |
|
~ |
~ |
~ |
|
F c v A c v ,c v 2 f,c v |
|||||
~ ~ |
~ |
~ |
Av,v |
~ |
|
Ac,c |
Ac,v Av,c |
2 f,c |
2 f,v . |
||
Учитывая симметрию матрицы A и вид функционала (4.29), запишем |
|||||
~ |
~ ~ |
~ |
|
~ |
|
F c v Ac,c 2 Ac,v Av,v |
2 f,c |
2 f,v |
|||
~ ~ |
~ |
|
|
|
~ |
Ac,c |
2 Ac,v f,v Av,v 2 f,c |
||||
118
