
Boyarshinov_ChM_T1
.pdf
xm ym,
xm 1 ym 1 cm 1mxm,
|
|
ym 1 cm 2mxm cm 2m 1xm 1, |
xm 2 |
||
|
|
m |
|
|
|
x1 |
y1 c1kxk . |
|
k 2
Таким образом, “прямой ход” метода Гаусса можно трактовать как преобразование
системы уравнений вида Ax = f в эквивалентную систему |
Ux = y, |
причем |
|||||||||||||||||||||||||||||
|
|
f |
|
|
|
|
|
|
|
f |
(1) |
|
|
f |
2 |
|
a |
21 |
y |
|
|
|
|
|
|
|
f(m 1) |
||||
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
m |
|
|
||||
y1 a11 |
, |
|
|
y2 |
|
a22(1) |
|
|
|
|
|
a221 |
|
, |
|
, |
ym a(mm m1) . |
||||||||||||||
Последнюю систему соотношений с учетом вышеприведенных выкладок можно |
|||||||||||||||||||||||||||||||
представить в иной форме |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f1 a11 y1 0 y2 0 y3 0 ym, |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a21 |
y1 |
|
a |
(1) |
y2 |
|
|
0 y3 |
0 ym, |
|
|
|
|
||||||||||||||||
f2 |
|
2 2 |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
y |
|
|
a |
(1) y |
|
|
a |
(2) |
y |
|
0 y |
|
, |
|
|
|||||||||||
f |
31 |
1 |
|
2 |
|
3 |
m |
|
|
||||||||||||||||||||||
|
3 |
|
|
|
|
|
|
32 |
|
|
|
|
|
|
33 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
y |
|
|
a(1) |
|
y |
|
|
a(2) |
y |
|
a(m 1) |
y |
|
|||||||||||||
f |
m 1 |
1 |
|
2 |
3 |
m |
|||||||||||||||||||||||||
m |
|
|
|
|
|
m 2 |
|
|
|
|
|
m 3 |
|
|
|
|
m m |
|
|||||||||||||
и записать в виде Ly = f , |
|
|
где |
|
L - нижняя треугольная матрица7 с отличными от нуля |
||||||||||||||||||||||||||
коэффициентами a(jjj 1) 0, |
j 1,m |
|
|
на главной диагонали. |
|
|
|
|
|
||||||||||||||||||||||
Все вышесказанное позволяет трактовать метод Гаусса как последовательное решение |
|||||||||||||||||||||||||||||||
двух систем уравнений: |
Ly = f |
|
и |
|
|
Ux = y . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Объединяя эти соотношения, получаем
LUx = f.
Сравнивая последнюю формулу с записью уравнения (2.1), можно сделать заключение,
что процедура метода Гаусса эквивалентна разложению исходной матрицы коэффициентов в произведение двух матриц специального вида:
L - нижняя треугольная матрица с ненулевыми коэффициентами на главной диагонали;
U - верхняя треугольная матрица с единицами на главной диагонали.
Обозначим угловые миноры матрицы А символами D j, j 1,m :
7 Обозначение матрицы L принято по первой букве английского слова lower - “нижний”.
21

D1 a11, |
|
|
|
|
|
a11 |
a12 |
|
|
D2 |
a21 |
a2 2 |
, |
|
|
a11 |
a12 |
a13 |
|
D3 |
a21 |
a2 2 |
a2 3 |
, |
|
a31 |
a32 |
a33 |
|
Dm det(A).
Теорема 2.1. Пусть все угловые миноры матрицы А отличны от нуля, D j 0, |
j 1,m . |
||||||||||||||||||
Тогда матрицу А можно представить единственным образом в виде |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
A = LU, |
|
|
(2.3) |
|
|
|
|
|||||
где L - нижняя треугольная матрица с ненулевыми диагональными элементами, U - верхняя |
|||||||||||||||||||
треугольная матрица с единицами на главной диагонали. |
|
|
|
|
|
|
|||||||||||||
Доказательство теоремы проводится по индукции. |
|
|
|
|
|
|
|||||||||||||
Рассмотрим разложение матрицы для простейшего случая m=2. Пусть в этом случае |
|||||||||||||||||||
матрицы имеют вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
11 |
a |
12 |
|
|
|
|
11 |
|
0 |
|
2 |
1 u |
12 |
|
|
|
||
A2 |
|
, |
L2 |
|
|
|
, U |
|
. |
|
|
||||||||
a21 |
a2 2 |
|
21 |
2 2 |
|
0 1 |
|
|
|
||||||||||
Предполагая разложимость для m=2, получаем систему уравнений относительно |
|||||||||||||||||||
коэффициентов матриц L2 |
и U2 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
A2 L2 U2 |
11 |
0 |
1 |
|
u12 |
11 |
|
11u12 |
|
|
|
||||||||
|
|
|
2 2 |
|
|
|
|
|
|
21u12 2 2 |
, |
|
|||||||
|
|
|
21 |
|
|
0 1 |
|
21 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
11 a11; |
11u12 a12; |
21 a21; |
21u12 2 2 a2 2. |
|
|
||||||||||||||
Решение этой системы уравнений дает значения коэффициентов: |
|
|
|
||||||||||||||||
11 a11 D1 0; |
21 a21; |
|
|
|
|
|
|
|
|||||||||||
|
|
a12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u12 |
a11 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2 |
a2 2 a21 |
a12 |
|
a11a2 2 a21a12 |
D |
2 0. |
|
|
|
|
|||||||||
a11 |
|
|
|
|
a11 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
D1 |
|
|
|
|
||||
Это означает, что возможность разложения (2.3), соответствующего условию теоремы,
показана для простейшего случая m=2. Теперь предположим, что условия теоремы
22
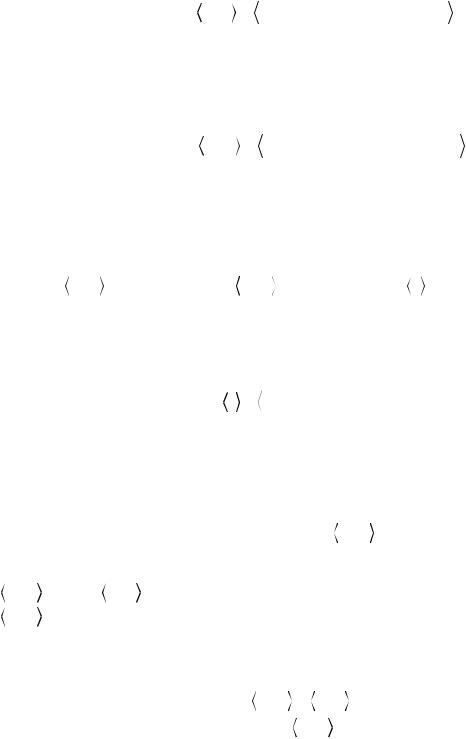
выполнены для случая (m-1), то есть имеет место разложение Am 1 Lm 1Um 1. Вводя обозначения
|
|
|
|
a1m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
am 1 |
|
|
|
|
|
, |
|
am 1 |
am1 am 2 |
|
am 3 am m 1 , |
|
||||||||||||
a3m |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
m 1m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
u1m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
u2 m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
um 1 |
|
u3 m |
|
, |
|
m 1 |
m 1 |
|
m 2 |
m 3 |
|
m m 1 , |
|
|||||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
m 1m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
представим матрицы Am, |
|
Lm, |
|
Um в форме |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
A |
|
|
a |
|
|
|
|
|
|
L |
|
|
|
0 |
|
|
|
|
U |
|
u |
|
||
Am |
|
m 1 |
|
m 1 , |
|
Lm |
|
m 1 |
|
|
|
, |
Um |
m 1 |
m 1 |
. |
||||||||
|
am 1 |
|
am m |
|
|
|
|
m 1 |
|
m m |
|
|
|
|
0 |
1 |
|
|||||||
Здесь принято, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
01 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
2 |
|
, 0 0 |
|
0 0 |
|
0 |
|
|
|
|
|||||||
|
|
|
|
|
0 |
|
1 |
3 |
m 1 . |
|
|
|||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0m 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Покажем существование |
|
разложения |
для |
матрицы |
Am . Перемножая Lm Um и |
|||||||||||||||||||
сравнивая результат со структурой матрицы Am , получаем систему (2m-1) алгебраических
уравнений относительно (2m-1) неизвестного um 1 , |
m 1 , |
m m : |
|||
|
|
|
|
|
|
Lm 1 um 1 am 1 , |
|
|
|
||
|
m 1 |
Um 1 am 1 , |
|
|
|
|
m 1 |
um 1 m m am m . |
|
|
|
|
|
|
|
||
В силу того, что det(Lm 1) 0, |
det(Um 1) 0 |
(треугольные матрицы с ненулевыми |
|||
значениями на главных диагоналях), существуют единственные решения первых двух
систем уравнений: um 1 Lm1 1 am 1 , |
m 1 |
am 1 Um1 1 . И, кроме того, может быть |
вычислено последнее неизвестное m m am m |
m 1 um 1 , значение которого должно |
|
быть отлично от нуля. Для того, чтобы убедиться в этом, произведем следующие выкладки:
det(A) det(Am ) det(LmUm ) det(Lm ) det(Um) m m det(Lm 1) det(Um 1).
23

В силу того, что det(A) 0, det(Lm 1) 0, det(Um 1) 1, имеет место равенство
det(A) lm m det(Lm 1), из которого сразу следует, что |
m m 0. При выполнении последних |
преобразований вновь учтено, что матрицы Lm, |
Um являются диагональными, а их |
определители представлены разложениями соответственно по последнему столбцу и нижней строке.
Покажем единственность разложения (2.3). Предположим, что такое разложение
возможно не единственным образом, то есть
A L(1)U(1) L(2)U(2) .
Проводя простейшие преобразования, получаем
L(1) L(2)U(2)U(11) ,
L(12)L(1) U(2)U(11) .
Можно заметить, что поскольку исходные и обратные матрицы сохраняют свою
“треугольную” форму, в левой части последнего выражения расположена нижняя
треугольная матрица, а в правой части - верхняя треугольная. Но равенство в этом случае
возможно лишь тогда, когда матрицы L(2)1 L(1) |
и U(2)U(11) |
являются диагональными. Более |
|||||
того, поскольку U(2) и U(11) |
содержат единицы на главной диагонали, полученные |
||||||
диагональные матрицы будут единичными, то есть L(2)1 L(1) |
U(2)U(11) E. А отсюда следует, |
||||||
что L(1) L(2), |
U(1) U(2) , но это и означает единственность разложения (2.3). |
||||||
Рассмотрим матрицу коэффициентов системы линейных алгебраических уравнений |
|||||||
следующего вида: |
|
|
|
|
|
|
|
|
|
1 |
1 |
0 |
|
|
|
|
А |
|
1 |
|
det(A) 1 0. |
||
|
1 |
1 , |
|||||
|
|
|
1 |
|
|
|
|
|
|
0 |
1 |
|
|
|
|
Первый шаг метода Гаусса приводит матрицу к виду |
|||||||
|
|
|
|
1 |
1 |
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
А 0 |
1 . |
|
||
|
|
|
|
|
1 |
|
|
|
|
|
|
0 |
1 |
|
|
Нулевое значение на главной диагонали матрицы вызывает аварийную остановку вычислительного процесса. Нетрудно убедиться, что для исходной матрицы А один из
угловых миноров D2 |
1 |
1 |
|
0, то есть имеется противоречие условиям теоремы 2.1. Для |
|
|
1 |
1 |
успешного выполнения процедуры метода Гаусса следует поменять местами строки матрицы А (смена столбцов приведет к необходимости изменить порядок неизвестных),
например:
24
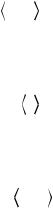
|
|
|
1 |
1 |
0 |
А |
* |
|
|
1 |
|
|
0 |
1 . |
|||
|
|
|
|
1 |
|
|
|
|
1 |
1 |
Приведение исходной матрицы к новому виду можно интерпретировать как некоторое преобразование вида A* P A. Для рассматриваемого случая
|
1 |
0 |
0 |
P |
|
0 |
|
0 |
1 . |
||
|
|
1 |
|
|
0 |
0 |
Теорема 2.2. Если определитель матрицы коэффициентов det(A) 0, то существует
матрица перестановок Р такая, что у матрицы |
A* P A все угловые миноры отличны от |
нуля. |
|
Доказательство теоремы проводится по индукции. |
|
Рассмотрим простейший случай - систему двух уравнений: |
|
a11 |
a12 |
A2 |
. |
a21 |
a22 |
Если a11 0, теорема справедлива при Р = Е , то есть в случае тождественного преобразования.
Пусть теперь a11 0. Поскольку det(A) a11a22 a12a21 a12a21 0, то a21 0.
Преобразуем исходную матрицу к виду
|
A2* |
|
a21 |
a22 |
|
|
0 |
1 |
||||
|
PA2 |
a12 |
|
, P |
|
. |
||||||
|
|
|
a11 |
|
|
|
1 |
0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
Теперь D1 a21 0, |
D2 a21a12 |
a11a22 |
0, то есть при m = 2 теорема справедлива. |
|||||||||
Пусть утверждение |
теоремы |
также верно |
и для |
Аm 1. Рассмотрим матрицу Аm |
||||||||
(обозначения введены ранее): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
a |
|
|
|
|
|
|
|
|
Am |
m 1 |
|
|
|
m 1 . |
|
|
|
||
|
|
|
am 1 |
|
am m |
|
|
|
|
|||
1. Рассмотрим случай det(Am 1) 0. Сформируем матрицу преобразования |
||||||||||||
|
|
|
P |
|
|
0 |
|
|
|
|
||
|
|
|
Pm |
m 1 |
|
|
|
|
|
|
||
|
|
|
|
0 |
|
|
1 |
|
|
|
|
|
|
|
и построим новую матрицу |
|
|
||||||||
|
|
|
|
A |
|
|
P |
a |
|
|
|
|
|
Am* |
|
P |
|
. |
|||||||
|
PmAm m 1 |
m 1 |
|
m 1 |
m 1 |
|
||||||
|
|
|
|
am 1 |
|
|
|
am m |
|
|
||
25
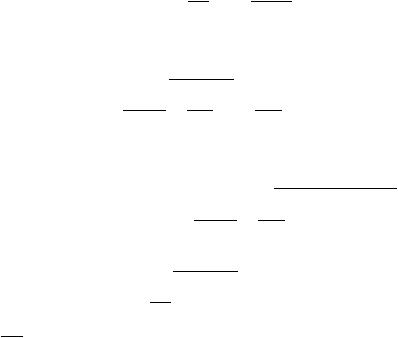
В силу сделанного предположения все угловые миноры матрицы Pm 1Am 1 отличны от нуля;
последний угловой минор Dm det(Am) det(A) 0 также отличен от нуля. В
рассмотренном частном случае теорема доказана.
2. Пусть теперь det(Am 1) 0.
Представим разложение определителя матрицы А в виде разложения по последнему
столбцу:
det(A) det(Am ) a1m det(A(m1) 1) a2m det(A(m2)1) am m det(A(mm)1) .
В силу det(A) 0, существует хотя бы один det(A(mk)1) 0. Поменяем местами строки матрица А с номерами m и k (m k в силу принятого условия det(Am 1) 0). В результате
получаем преобразованную матрицу A |
* |
P A |
m |
, у которой угловой минор |
D* |
det(A* |
) |
|
m |
m |
|
m 1 |
m 1 |
|
|
отличен от нуля. Теперь, в соответствии с доказательством случая 1, уже все угловые |
|
||||||
миноры матрицы Am* |
отличны от нуля. |
|
|
|
|||
Следствие. Если det(A) 0, то |
|
существует матрица перестановок |
Р |
такая, что |
|||
справедливо разложение
PA = LU,
где L - нижняя треугольная матрица с ненулевами коэффициентами на главной диагонали; U - верхняя треугольная матрица с единицами на главной диагонали.
Определение числа операций алгоритма метода Гаусса
Подсчитаем число операций умножения и деления (наиболее длительные операции
при вычислениях на ЭВМ), |
необходимое для реализации алгоритма метода Гаусса. |
|
||||
1. |
Вычисление |
коэффициентов |
ci j, i 1,m, |
j i 1,m |
(сумма |
членов |
арифметической прогрессии): |
|
|
|
|
||
(m 1) (m 2) 1 m (m 1) . 2
2. Вычисление коэффициентов a(ikj), k 2,m, i k,m, j k,m (сумма слагаемых арифметической прогрессии 2-го порядка [6]):
(m 1) (m 1) (m 2) (m 2) 1 1 1 22 (m 1)2 m (m 1) (2m 1) . 6
3. Вычисление значений fi(k), k 2,m, i k,m :
(m 1) (m 2) 1 m (m 1) . 2
4. Вычисление значений yi, i 1,m производится m раз. 5. Вычисление xi, i 1,m при “обратном ходе” метода Гаусса:
26

1 2 (m 1) m (m 1) . 2
Общее количество операций умножения и деления определяется суммой всех определенных выше выражений:
m 3 |
m (m 1) |
|
m (m 1) (2m 1) |
|
m |
m |
2 |
3m 1 . |
2 |
6 |
3 |
|
Иными словами, количество операций умножения и деления приблизительно
пропорционально m3 , что и определяет затраты на выполнение метода Гаусса. 3
Вычисление определителя матрицы
Вычитание строк в методе Гаусса (образование линейных комбинаций уравнений) не изменяет значения определителя матрицы [7]. Знак определителя может измениться лишь при использовании процедуры выбора “главного” элемента, когда производится перестановка строк (столбцов) преобразуемой матрицы. В результате выполнения всех необходимых преобразований метода Гаусса определитель исходной матрицы может быть вычислен достаточно просто:
m
det(A) det(LU) det(L) det(U) det(L) ajjj 1 .
j 1
Здесь учтено, что L и U - треугольные матрицы и, кроме того, матрица U содержит только единицы на главной диагонали.
Таким образом, сохраняя значения коэффициентов, расположенных после преобразования уравнений (до операции деления коэффициентов строки на первый ненулевой элемент) на главной диагонали, можно вычислить определитель исходной матрицы.
Построение обратной матрицы
Пусть pq, |
p,q 1,m |
- |
коэффициенты |
|
обратной матрицы A 1 . Согласно |
|
определению |
|
|
|
|
|
|
|
m |
|
|
1, i j |
|
|
|
ai k k j |
|
|
|
|
|
|
i j, |
i j |
0, i j |
- |
символ Кронекера8. |
|
|
k 1 |
|
|
|
|
|
8 Кронекер Леопольд [7.12.1823 - 29.12.1891] - немецкий математик. С 1861 года - член Берлинской академии наук; с 1872 года стал членом-корреспондентом Петербургской академии наук. В 1883 году занял должность профессора Берлинского университета.
27
Теперь q-й столбец p(q) обратной матрицы можно рассматривать как результат решения системы линейных алгебраических уравнений вида
1(q) |
|
0(1) |
|
|||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
2(q) |
|
(2) |
|||
|
|
|
|
|
|
|
A |
|
|
. |
|||
p(q) |
1(q) |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
0 |
|
|
|
m(q) |
|
(m) |
|||
|
|
|||||
Таким образом, для нахождения обратной матрицы необходимо решить m систем линейных алгебраических уравнений с правыми частями, определенными специальным образом. При этом матрицу коэффициентов следует преобразовать лишь один раз, но одновременно преобразовывать m правых частей всех систем уравнений.
28
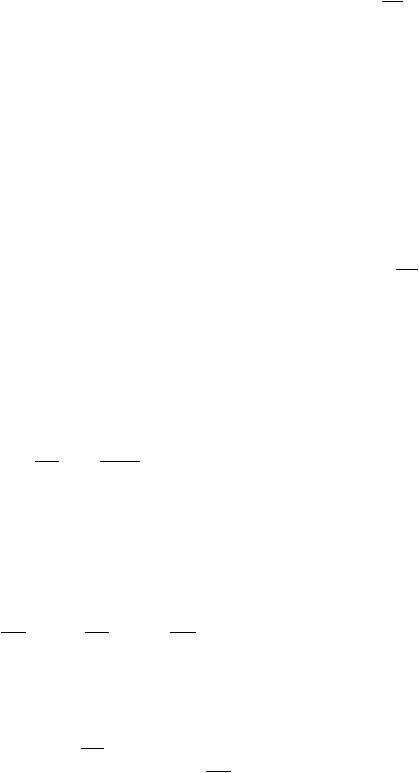
Метод квадратного корня
Метод квадратного корня предназначен для решения систем линейных алгебраических
уравнений вида Ax = f с симметричной матрицей коэффициентов ai j aji, |
i, j 1,m . |
Метод основан на разложении матрицы коэффициентов А в произведение |
|
A ST D S, |
(2.4) |
где S - верхняя треугольная матрица с положительными значениями на главной диагонали; D - диагональная матрица со значениями +1 или -1.
Согласно теореме 2.1 при неравенстве нулю всех угловых миноров матрицу А можно разложить в произведение A = LU.
Представим нижнюю треугольную матрицу L |
с ненулевыми коэффициентами на |
|||||||||||||||||||||
главной диагонали в виде произведения |
N K, |
|
где |
N - нижняя треугольная матрица с |
||||||||||||||||||
единицами на главной диагонали, |
|
К - диагональная матрица, причем ki i |
ii, |
i 1,m : |
||||||||||||||||||
11 |
0 |
|
0 |
|
0 |
|
|
1 |
|
0 |
|
0 |
|
0 |
11 |
0 |
|
0 |
0 |
|
||
|
|
|
|
0 |
|
0 |
|
|
|
|
1 |
|
0 |
|
0 |
|
|
|
|
0 |
0 |
|
|
21 |
22 |
|
|
|
n |
21 |
|
|
0 |
2 2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
L |
31 |
32 |
33 |
0 |
|
n |
31 |
n32 |
1 |
|
0 0 |
0 |
|
33 |
0 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
n |
|
n |
|
1 |
|
|
0 |
|
0 |
|
|
|
m1 |
m 2 |
m 3 |
m m |
|
n |
m1 |
m 2 |
m 3 |
0 |
|
mm |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
После перемножения |
матриц |
|
||||
относительно величин ni j, |
|
i 2,m, |
|
|||
21 |
n21 11; |
|||||
|
|
|
|
|
|
|
|
31 |
n31 11, |
||||
|
||||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
, |
|
41 |
41 |
11 |
|||
|
|
|
|
|||
N и K получаем систему линейных уравнений j 1,m 1:
32 n32 22;
42 n42 22, |
4 3 n43 33. |
Очевидно, что |
n21 |
21 , n |
31 |
31 , |
n32 |
32 , |
|
||||
|
|
|
11 |
|
|
11 |
|
|
2 2 |
|
|
|
|
|
|
|
|
|
|
||||
С учетом этого коэффициенты ni j, |
|
ki j матриц N |
и K можно представить в общем |
||||||||
виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i j |
, |
j i |
|
|
|
|
|
|
|
|
|
j j |
|
|
|
|
|
|
|
|
|
ni j |
|
1, |
|
|
j i |
, i 2,m; |
||
|
|
|
|
|
|
||||||
|
|
|
|
|
0, |
|
|
j i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30
