
Boyarshinov_ChM_T1
.pdf
Пусть рассматривается система линейных алгебраических уравнений Ax = f с
симметричной положительно определенной матрицей А. Решение будем искать с помощью явного нестационарного метода Ричардсона,
|
|
|
|
|
x(n 1) |
x(n) |
Ax(n) f, |
n 0,1, |
|
|
|
|
|||||
|
|
|
|
|
|
(n 1) |
|
|
|
|
|
|
|
|
|
||
Попытаемся |
так |
определить |
|
набор |
(1), (2), , (N) , |
чтобы |
x(N) x |
была |
|||||||||
минимальной для заданного числа итераций N. |
|
|
|
|
|
|
|
||||||||||
Теорема |
2.6. |
|
Пусть А - симметричная положительно определенная матрица, |
||||||||||||||
min 0, max |
0 - |
наименьшее и наибольшее собственные значения. Пусть задано число |
|||||||||||||||
итераций N. Среди всех наборов (n), |
n 1,N , наименьшую погрешность |
x(N) x |
имеет |
||||||||||||||
набор, для которого |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
(n) |
|
|
(0) |
, |
n 1,N; |
|
|
|
|
|
|
|
||||
|
1 0t(n) |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
(0) |
|
|
2 |
|
; |
|
|
1 ; |
min ; |
t(n) cos |
2n 1 |
|
|
|||
|
min |
|
0 |
. |
|
|
|||||||||||
|
|
|
max |
|
|
|
1 |
max |
|
|
2N |
|
|
||||
Оценка погрешности в этом случае имеет вид:
x(N) x |
q(N) x(0) x , |
q(n) |
2 N |
, |
|
|
1 |
|
1 |
1 |
. |
||||||
|
|
|
1 12N |
|
1 |
|
|
Доказательство. Введем, как и ранее, погрешность решения z(n) x(n) x . Схема Ричардсона позволяет записать систему уравнений относительно погрешностей:
z(n 1) z(n) |
Az(n) 0, |
n 0,N 1. |
(n 1) |
|
|
Отсюда получаем
z(n 1) z(n) (n 1)Az(n) E (n 1)A z(n) .
В частности,
z(1) E 11)A z(0) ,
z(2) E (2)A z(1) E (2)A E (1)A z(0),
|
. . . |
N |
|
z(N) E (n)A z(0) . |
|
n 1 |
|
Обозначим
61

N
T(N) E (N)A E (N 1)A E (1)A E (n)A . n 1
Понятно, что T(N) - симметричная матрица. Теперь погрешность на N итерации можно представить выражением
z(N) T(N)z(0), |
z(N) T(N)z(0) . |
Для симметричной положительно определенной матрицы в качестве нормы может быть выбран спектральный радиус max(T(N)) . В самом деле, для собственного вектора m, соответствующего собственному значению max ,
T(N) max ,
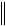 T(N)
T(N) 
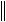 max
max 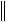
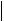 max
max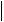
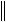
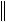
 .
.
Сучетом свойств нормы получаем

 T(N)
T(N) 
 T(N)
T(N)

 ,
,
|
T(N) . |
(2.19) |
С другой стороны, пусть k , |
k 1,m - ортонормированная |
система векторов, |
построенная на основе собственных векторов матрицы T(N) ,
m
k, n ik ni k n . i 1
Разложим вектор m по этому базису:
m
ck k .
k 1
Согласно определению нормы вектора
2m m m m
, ck k, cn n ck ikk 1 n 1 i 1 k 1
m |
|
m |
m |
|
|
cn in |
|
ckcn ik in |
|||
n 1 |
|
|
i 1 |
|
|
|
k,n 1 |
|
|
||
mm
ckcn k n c2k .
k,n 1 k 1
В компонентной записи вектор T(N) с использованием собственных чисел и
векторов выглядит следующим образом:
T(N) i |
m |
m |
|
Ti(N)j |
j Ti(N)j |
||
|
j 1 |
j 1 |
|
m |
|
m |
m |
kj |
|
m |
ck kj |
|
ck |
Ti(N)j |
|
ck k ik . |
|
k 1 |
|
k 1 |
j 1 |
|
|
k 1 |
Здесь использовано определение собственных значений и векторов:
62

|
|
T(N) k |
k k . |
|
|
|
|
|
|
|
|
|
|
Учитывая, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
m |
m |
|
m |
in |
|
|
m |
|
m |
|
|
|
T(N) |
T(N) ,T(N) ck k ik cn n |
|
ckcn |
k n ik in |
|
||||||||
|
i 1 |
k 1 |
|
n 1 |
|
|
|
k,n 1 |
|
i 1 |
|
|
|
|
m |
|
m |
|
|
|
m |
|
|
|
|
|
|
|
ckcn k n k n |
c2k 2k 2max c2k |
2max |
2 |
, |
|
|
||||||
|
k,n 1 |
|
k 1 |
|
|
k 1 |
|
|
|
|
|
||
можно подсчитать норму оператора |
|
|
|
|
|
|
|
|
|
|
|
||
|
T(N) |
T(N) |
sup |
|
max |
|
. |
|
|
|
|
||
|
sup |
|
|
|
|
|
|
|
|||||
|
H, 0 |
H, 0 |
|
|
|
|
|
|
|
|
|
||
Сравнивая последнее неравенство с выражением (2.19), определяем точное значение нормы:
 T(N)
T(N) .
.
С учетом этого можно оценить величину погрешности:
|
|
|
|
|
|
|
|
|
|
|
|
z(N) T(N)z(0) z(0) . |
|
|
|
|||
|
|
|
|
Построение |
|
доказательства |
теоремы |
2.6 |
основано |
на поиске |
такого |
набора |
||||||
(n), |
n 1,N , который минимизирует спектральный радиус матрицы T(N) . |
|
||||||||||||||||
|
|
|
|
Предположим, что все собственные значения матрицы А упорядочены: |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 1 |
min |
2 |
m 1 m |
max . |
|
|
|
|
|
|
|
Известно |
[7], |
что если |
f(A) - матричная |
функция |
матричного |
аргумента |
А, то |
|||||||
f |
|
|
1 |
,f |
|
|
, , f |
|
|
m - полная система собственных значений матрицы f(A). |
|
|||||||
|
|
|
|
2 |
|
|
||||||||||||
Поскольку
T(N) A E (N)A E (N 1)A E (1)A
является как раз матричной функцией матричного аргумента, то соответствующая скалярная функция
1 (N) i 1 (N 1) i 1 (1) i
определяет собственные значения матрицы T(N) . В этом случае ее спектральный радиус может быть определен как
(N) (N 1) (1)
max 1 i 1 i 1 i .
1 i m
Обозначим
63

f 1 (N) 1 (N 1) 1 (1) . |
(2.20) |
|||||||||
Тогда спектральный радиус можно определить следующим образом: |
|
|||||||||
|
|
|
|
max |
f( ) |
|
|
|
||
|
|
|
min max |
|
|
|
|
|
|
|
и определение набора (n), |
n 1,N сводится к задаче поиска |
|
|
|||||||
|
min |
max |
f |
min |
f |
. |
|
|||
|
n ,n |
1,N |
min max |
|
n ,n |
1,N |
|
|
||
Очевидно, что функция (2.20) является полиномом степени N, причем f(0) = 1. Иначе говоря, поиск итерационных параметров (n), n 1,N сводится к задаче об отыскании полинома степени N, наименее уклоняющегося от нуля на отрезке min, max , которая может быть решена с использованием полинома Чебышёва.
Корни функции (2.20) принимают значения:
|
|
|
1 (n) 0, |
n |
1 |
, n 1,N |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
(n) |
|
|
|
|
|
|
и должны совпадать с корнями полинома Чебышёва: |
|
|
|
|
|||||||||||||
n |
max min |
max min cos 2n 1 , |
n 1,N . |
||||||||||||||
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
2N |
|
|
|
|
Теперь очевидно, что итерационные параметры следует выбирать следующим образом: |
|||||||||||||||||
(n) 1 |
n |
max min |
max |
min |
cos 2n 1 |
||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
2N |
|
|
|
|
|
|
|
|
|
|
min t |
|
1 |
1 |
|
||||
|
max |
2 |
min 1 |
|
max |
|
(n) |
|
1 |
|
t(n) |
, |
|||||
|
|
|
|
|
max |
min |
|
|
(0) |
|
1 |
|
|||||
|
|
|
|
|
(n) |
|
(0) |
|
, |
n 1,N. |
|
|
|
||||
|
|
|
|
|
|
|
|
1 0t(n) |
|
|
|
|
|
|
|
||
Обозначения соответствуют введенным при формулировке теоремы. |
|||||||||||||||||
Для оценки нормы погрешности заметим, что |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
max |
f( ) f |
2 N |
|
|
|
||||||
|
|
|
|
|
|
12N , |
|
|
|
||||||||
|
|
|
|
|
min max |
|
|
|
1 1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
откуда получаем z(N) |
|
2 N |
z(0) . |
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 2N |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Что и требовалось доказать.
Неявный метод с чебышёвским набором параметров
64

Рассмотрим неявную итерационную схему с положительно определенными матрицами А и В:
x(n 1) |
x(n) |
Ax(n) f . |
(2.21) |
B |
|
||
(n 1) |
|
|
|
Эта система уравнений для погрешностей принимает вид |
|
||
Bz(n 1) |
z(n) |
Az(n) 0. |
|
(n 1) |
|
|
|
Указанные свойства матрицы В позволяют представить ее в виде B B1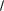 2B1
2B1 2 . Тогда предыдущее соотношение можно представить в форме
2 . Тогда предыдущее соотношение можно представить в форме
B1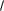 2z(n 1) B1
2z(n 1) B1 2z(n) B 1
2z(n) B 1 2Az(n) 0.
2Az(n) 0.
(n 1)
|
Обозначим B1 2z(n) |
v(n), |
z(n) B 1 2v(n) . Тогда |
|
|
|
v(n 1) v(n) Cv(n) 0, |
|
|
|
(n 1) |
где |
C B 1 2AB 1 2 - |
симметричная положительно определенная матрица, причем |
|
минимальное (максимальное) собственное значение матрицы B 1A является одовременно и минимальным (максимальным) собственным значением для матрицы С.
Теорема 2.7. Пусть А и |
В - симметричные и положительно определенные матрицы. |
min, max - наименьшее и |
наибольшее собственные значения матрицы B 1A . Для |
заданного числа N итераций неявный чебышёвский метод (2.21) имеет минимальную |
|
погрешность при наборе (n), |
n 1,N , определенном условиями предыдущей теоремы, где |
min B 1Amax B 1A .
Удачным выбором матрицы В можно приблизить значение параметра к 1, что приведет к понижению погрешности 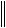 z(N)
z(N)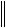 .
.
65

Метод минимальных невязок
Погрешность z(n) x(n) x решения системы линейных алгебраических уравнений вида14 Ax = f определить невозможно, поскольку точное решение x неизвестно. Однако можно оценить невязку
r(n) Az(n) A x(n) x Ax(n) Ax Ax(n) f ,
определяющую, насколько полученное решение не удовлетворяет исходному уравнению.
Рассмотрим явный итерационный метод:
x(n 1) x(n)
(n 1) Ax(n) f .
Определим из этого соотношения величину x(n 1) :
x n 1 x n n 1 Ax n f x n n 1 r n .
При использовании итерационной схемы для (n+1) шага следует так подобрать
итерационный параметр (n 1) , |
чтобы при известном x(n) |
значение невязки r(n 1) стало |
наименьшим. |
|
|
Оценим невязку для следующего шага: |
|
|
r(n 1) Ax(n 1) f Ax(n) (n 1)Ar(n) f r(n) (n 1)Ar(n) . |
||
Определим, как и ранее, квадрат нормы невязки: |
|
|
r(n 1) 2 |
r(n) (n 1)Ar(n), r(n) (n 1)Ar(n) |
|
r(n), r(n) (n 1)Ar(n), r(n) r(n), (n 1)Ar(n) (n 1)Ar(n), (n 1)Ar(n) |
||
r(n) 2 |
2 (n 1) r(n), Ar(n) (n 1) 2 |
Ar(n) 2. |
При выводе последнего выражения учтено, что
Au, v u, ATv u, Av ,
AT A - в силу симметрии матрицы.
Полученное соотношение между невязками на соседних шагах итерационной
процедуры можно рассматривать как функциональную зависимость |
r(n 1) (n 1) . Для |
нахождения значения итерационного параметра, при котором невязка |
r(n 1) минимальна, |
воспользуемся теоремой Ферма15 : |
|
14 Здесь и далее предполагается, что А - симметричная, положительно определенная матрица.
66

d r(n 1) 2 |
2 r(n), Ar(n) 2 (n 1) Ar(n) |
2 |
, |
|
d (n 1) |
0 |
|||
|
(n 1) |
r(n), Ar(n) |
|
|
|
|
|
|
|
|
|
Ar(n) 2 . |
|
|
Оценка невязки получаемого решения:
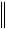 A x(n) x
A x(n) x 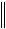 0n
0n 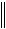 A x(0) x
A x(0) x 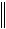 .
.
Здесь |
0 |
1 |
; |
min ; |
min, max - наименьшее и наибольшее собственные |
|
|
1 |
|
max |
|
значения матрицы А; n - номер итерации.
Метод минимальных поправок
Неявную итерационную схему
Bx(n 1) |
x(n) |
Ax(n) f |
(n 1) |
|
|
можно представить виде |
|
|
Bx(n 1) |
x(n) |
r(n) 0, |
(n 1) |
|
|
x(n 1) x(n) (n 1)B 1r(n), |
||
где, как и ранее, r(n) Ax(n) f . Вектор |
w(n) B 1r(n) назовем поправкой. Очевидно, что |
|
поправка w(n) удовлетворяет уравнению |
|
|
Bw(n 1) w(n) |
Aw(n) 0. |
|
(n 1) |
|
|
Предполагая, что В - симметричная положительно определенная матрица, определим норму в виде
v B |
Bv, v . |
|
Подсчитаем значение квадрата нормы поправки w(n 1) |
w(n) (n 1)B 1Aw(n) : |
|
w(n 1) 2 B w(n) (n 1)B 1Aw(n) , w(n) (n 1)B 1Aw(n) B
15 Пьер Ферма [17.8.1601-12.1.1665] - французский математик. По профессии был юристом, с 1631 года являлся советником парламента в Тулузе. Основные научные труды изданы лишь после его смерти.
Теорема Ферма [10]: пусть функция y = f(x), непрерывная в некотором замкнутом интервале [a, b], принимает свое наименьшее (наибольшее) значение во внутренней точке этого интервала. Если в точке производная функции f(x) существует, то она равна нулю.
67
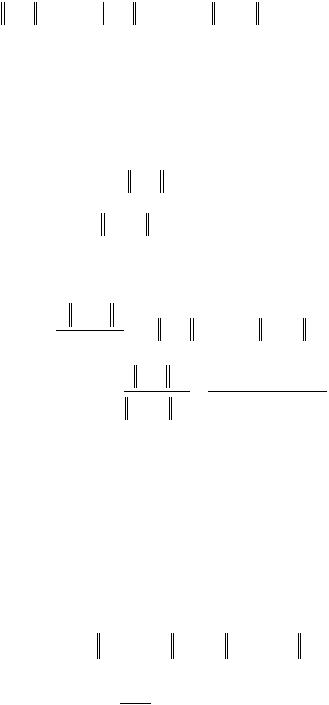
Bw(n), w(n) (n 1) Aw(n), w(n) (n 1) Bw(n), B 1Aw(n) (n 1) 2 Aw(n),B 1Aw(n) |
|||
Bw(n), w(n) 2 (n 1) Aw(n), w(n) (n 1) 2 Aw(n), B 1Aw(n) |
|||
2 |
2 |
2 |
2 |
w(n) B 2 (n 1) w(n) |
A (n 1) |
Aw(n) |
B 1 . |
При получении последнего выражения использовались следующие соотношения:
n |
1 |
n |
|
|
|
1 |
T |
n |
|
n |
1 |
n |
|
n |
n |
n |
|
Bw |
,B Aw |
|
|
|
B |
|
A Bw |
|
,w |
|
AB Bw |
|
,w |
|
Aw ,w |
|
, |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
AT A, B 1 T |
B 1 , |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
w(n) |
2 |
Aw(n), w(n) , |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Aw(n) 2 1 |
Aw(n), B 1Aw(n) . |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
Очевидно, что величина 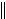 w(n 1)
w(n 1)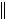 будет минимальной при условии
будет минимальной при условии
B
d w(n 1) |
2 |
|
|
|
|
|
|
|
B 2 w(n) |
2 |
2 (n 1) Aw(n) 2 |
0, |
|||||
d |
(n 1) |
|
|
|
|
A |
B 1 |
|
|
|
|
|
|
|
|
|
|
(n 1) |
|
w(n) |
2 |
|
|
Aw(n), w(n) |
|
|
|
Aw(n) |
A2 |
1 |
Aw(n), B 1Aw(n) . |
||||
|
|
|
|
B |
|
|
|
|
Для реализации метода минимальных поправок требуется на каждой итерации решать систему уравнений Bw(n) r(n) , откуда находится сама поправка w(n) . Кроме этого необходимо определить решение системы уравнений Bv(n) Aw(n) , а именно, вычислить v(n) B 1Aw(n) , требующееся для нахождения итерационного параметра.
Погрешность метода минимальных поправок оценивается следующим образом (с
учетом введенного определения нормы):
|
|
|
A x(n) x |
B |
1 |
0n |
A x(0) x |
B |
1 . |
|
|
|
|
|
|
|
|
||
Как и ранее, 0 |
1 |
; |
min ; |
min, max - наименьшее и наибольшее собственные |
|||||
|
1 |
|
max |
|
|
|
|
|
|
значения матрицы B 1A ; n - номер итерации.
Метод скорейшего спуска
68

Относительно погрешности z(n) x(n) x итерационная схема Ричардсона, как это было уже показано ранее, принимает вид:
z(n 1) z(n) Az(n) 0.(n 1)
Отсюда, погрешность
|
z(n 1) |
z(n) |
(n 1) Az(n) . |
Определим выражение |
|
|
|
z(n 1) |
2A Az(n 1), z(n 1) A z(n) (n 1)Az(n) , z(n) (n 1)Az(n) |
||
Az(n), z(n) A (n 1)Az(n), z(n) Az(n), (n 1)Az(n) A (n 1)Az(n), (n 1)Az(n)
Az(n), z(n) 2 (n 1) Az(n), Az(n) (n 1) 2 A2z(n), Az(n)
|
2 |
2 |
|
2 |
2 |
z(n) |
A 2 (n 1) Az(n) |
(n 1) |
Az(n) |
A. |
При выводе последнего соотношения использована симметричность матрицы А,
AAz(n), z(n) Az(n), Az(n) .
Полученное выражение может рассматриваться как квадратичная функция итерационного параметра (n 1) . Воспользуемся теоремой Ферма для нахождения значения итерационного параметра, доставляющего экстремум этому выражению,
|
|
|
d |
z(n 1) 2 |
|
|
|
2 |
|
Az(n) |
2 |
0, |
||
|
|
|
|
d |
(n 1) |
A 2 Az(n) |
2 (n 1) |
A |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(n 1) |
Az(n) |
2 |
|
Az(n), Az(n) |
|
|
|||||
|
|
|
Az(n) |
2 A2z(n), Az(n) . |
|
|
||||||||
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
Вторая производная |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
d2 z(n 1) 2 |
2 Az(n) |
2 |
0 |
|
|
|||
|
|
|
|
|
|
d (n 1) |
A |
A |
|
|
||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
положительна в силу |
положительной |
|
определенности |
А, то есть выражение |
||||||||||
z(n 1) |
2 |
Az(n 1), z(n 1) |
принимает наименьшее значение при найденном (n 1) . |
|||||||||||
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
69

Вспоминая, что Az(n) r(n) - невязка решения системы уравнений, получаем
|
(n 1) |
r(n) |
2 |
|
|
|
2 . |
|
|
|
|
r(n) |
A |
|
|
|
|
|
|
Погрешность решения системы линейных алгебраических уравнений методом |
||||
скорейшего спуска оценивается выражением |
|
|
||
x(n) x |
0n x(0) x |
, 0 |
1 , |
min , |
|
A |
A |
1 |
max |
|
|
|
||
где min , max - наименьшее и наибольшее собственные значения матрицы А; n - номер итерации.
Неявный метод скорейшего спуска
Рассмотрим неявную итерационную схему вида
Bx(n 1) x(n) Ax(n) f
(n 1)
с симметричной и положительно определенной матрицей B.
Для погрешности z(n) x(n) x эта схема принимает следующую форму:
|
B |
z(n 1) z(n) |
Az |
(n) |
0. |
|
(n 1) |
|
|||
Отсюда, z(n 1) |
z(n) (n 1)B 1Az(n) . |
|
|
|
|
Как и ранее, с учетом симметрии матрицы А, определим выражение
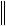 z(n 1)
z(n 1) 2A Az(n 1), z(n 1)
2A Az(n 1), z(n 1)
Az(n), z(n) 2 (n 1) Az(n), B 1Az(n) (n 1) 2 AB 1Az(n), B 1Az(n)
|
|
2 |
2 |
(n 1) |
2 |
2 |
|
z(n) |
A 2 (n 1) Az(n) |
B 1 |
B 1Az(n) |
A. |
Благодаря положительной определенности матрицы А,
Az(n 1), z(n 1) 0,
минимум полученного выражения достигается при значении итерационного параметра
70
