
Boyarshinov_ChM_T1
.pdf
Rn полную ортонормированную систему, которую можно использовать в качестве базиса.
Очевидно, что для симметричных матриц Xi Yi . А значит, имеет место устойчивость собственных значений:
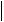 d i
d i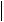
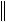 dA
dA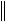 .
.
Для оценки устойчивости собственных векторов теперь рассмотрим случай i j. В
силу формулы (5.3) следует
A Xi ,Y j Xi ,ATY j Xi , jY j j Xi ,Y j .
Используя это выражение и условие ортогональности векторов
Xi ,Yj 0, i j,
из соотношения (5.4) получаем
A Xi ,Y j i Xi ,Y j j Xi ,Y j ,
Xi ,Y j A Xi ,Y j .
i j
Разложим вектор Xi по базису Xk , k 1,n :
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
Xi ik Xk . |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
Вычислим скалярное произведение |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
Xi ,Yp |
ik Xk,Yp |
|
ik Xk,Yp ip Xp,Yp , |
||||||||||||
|
|
k 1 |
|
|
|
|
|
|
k 1 |
|
|
|
|
|||
которое позволяет получить выражение для коэффициентов разложения ij : |
||||||||||||||||
|
|
ip |
Xi ,Yp |
|
|
|
A Xi ,Yp |
, i p. |
|
|||||||
|
|
Xp,Yp |
Xp,Yp i p |
|
||||||||||||
|
|
|
|
|
|
|
|
|||||||||
В случае |
i = p |
за счет произвола в выборе длины собственных векторов можно |
||||||||||||||
положить ip |
0. Теперь разложение вектора Xi |
по базису Xk, |
k 1,n |
имеет вид |
||||||||||||
|
|
|
|
|
|
n |
|
A Xi ,Yk |
|
|
|
|||||
|
|
|
Xi |
|
|
|
k |
,Y |
k |
i |
Xk . |
|
|
|||
|
|
|
|
|
k 1,k i X |
|
|
k |
|
|
|
|||||
Оценим приращение вектора Xi : |
|
|
|
|
|
|
|
|
|
|
||||||
|
n |
A Xi |
Yk |
Xk |
|
|
|
|
n |
|
Yk Xk |
|
||||
Xi |
Xk,Yk i |
k |
|
|
A Xi |
,Yk i |
, |
|||||||||
|
k 1,k i |
|
|
|
|
|
k 1,k i Xk |
k |
||||||||
129
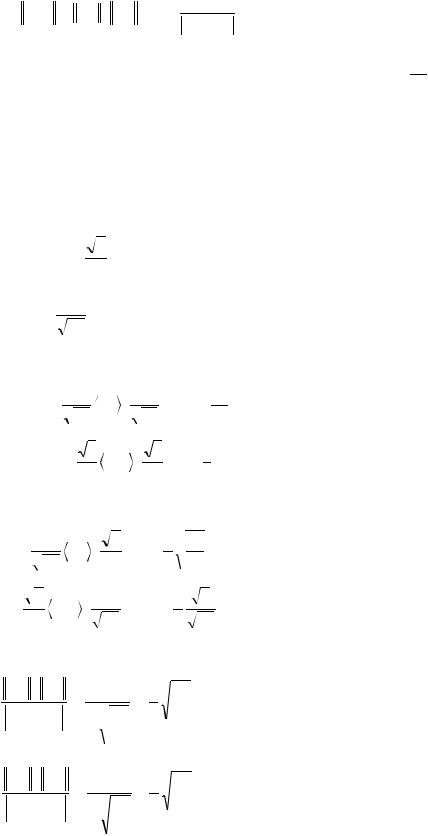
|
|
|
n |
Ck . |
Xi |
A Xi |
|
|
|
|
|
|
k 1,k i i |
k |
Отсюда очевидно, что неустойчивость собственных векторов имеет место в случае,
когда велики коэффициенты перекоса Ck , либо близки собственные значения k, k 1,n .
Пример 5.2. Рассмотрим матрицу A, |
указанную в примере 5.1. Нетрудно убедиться, |
||||||||||
что для транспонированной матрицы |
AT |
1 |
5 |
|
|||||||
|
собственные числа остаются теми же, |
||||||||||
|
|
|
|
|
|
|
|
|
2 |
4 |
|
1 6, |
2 |
1, а соответствующие |
собственные |
векторы определяются следующим |
|||||||
образом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
1 |
|
2 1 |
0707106781, |
|||
|
|
|
|
|
2 |
|
, |
||||
|
|
|
|
|
|
|
1 |
0707106781, |
|||
|
|
Y |
2 |
|
|
1 |
5 |
0928476691, |
|||
|
|
|
|
|
|
|
|
|
. |
||
|
|
|
|
|
|
29 |
2 |
0371390676, |
|||
Перемножим скалярно собственные векторы обеих матриц:
X1 |
1 |
25, |
1 |
5 |
|
1 |
0 0, |
||
,Y2 |
29 |
|
|
29 |
|||||
|
29 |
|
2 |
|
|
|
|||
X2,Y1 2 |
11, |
|
1 |
|
1 0 |
0, |
|||
2 |
|||||||||
|
2 |
|
2 |
1 |
|
|
2 |
|
|
то есть имеет место ортогональность собственных векторов матриц A и AT ;
X1,Y1 |
1 |
25, |
2 |
1 |
|
7 |
2 |
091914503,, |
|
||||||||
|
29 |
2 |
1 |
|
2 |
29 |
|
|
X2,Y2 |
2 |
11, |
1 |
5 |
7 |
2 |
091914503,. |
|
|
|
|||||||
|
2 |
|
29 |
2 |
2 |
29 |
||
Подсчитаем коэффициенты перекоса:
С1 |
|
X1 Y1 |
|
|
|
1 1 |
|
2 |
29 |
1087967587,, |
||||
X1,Y1 |
7 |
|
2 |
|
7 |
2 |
||||||||
|
|
|
|
2 |
29 |
|
|
|
|
|
||||
С2 |
|
X2 Y2 |
|
|
|
|
1 1 |
|
2 |
29 |
1087967587,. |
|||
X2,Y2 |
|
7 |
|
|
2 |
|
7 |
2 |
||||||
|
|
|
|
2 |
29 |
|
|
|
|
|||||
Пример 5.3. Оценить влияние погрешности на результаты вычисления собственных
значений матрицы
130

1 |
1 |
0 |
0 |
|
|
|
|
|
|
A 0 |
2 |
1 |
0 |
, |
0 |
0 |
3 |
1 |
|
|
0 |
0 |
|
|
|
4 |
|
где e - малое возмущение (погрешность).
Решение характеристического уравнения
det A E 1 2 3 4 0.
дает корни (собственные значения):
1 25. 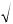 5 4
5 4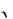 1 , 2
1 , 2
2 25. 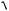
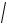 5 4
5 4
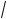 1 , 2
1 , 2
3 25. 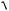
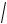 5 4
5 4 1 , 2
1 , 2
4 25.  5 4
5 4 1 . 2
1 . 2
В табл. 5.1 приведены собственные значения исходной матрицы при различных величинах e.
Таблица 5.1
Определение собственных значений матрицы при заданных величинах погрешности
Собственные значения |
e = 0 |
e = 0,1 |
e = 0,01 |
e = 0,001 |
|
|
|
|
|
1 |
1,0 |
0,983817673 |
0,9983384 |
0,999833384 |
2 |
2,0 |
2,051456633 |
2,005012689 |
2,000500125 |
3 |
3,0 |
2,948543367 |
2,994987311 |
2,999499875 |
4 |
4,0 |
4,016182327 |
4,0016616 |
4,000166616 |
|
|
|
|
|
Определение собственных значений и векторов
Метод интерполяции
131
Пусть задана матрица А размером n n. Очевидно, что характеристический многочлен в этом случае имеет порядок n (полином степени n), и задача заключается в определении
корней этого полинома.
Алгоритм вычисления собственных значений матрицы А следующий:
1. Строится функция f det A E : |
|
|
|
|
||
- на числовой оси выбирается (n+1) значений k, |
k 0,n ; |
|||||
- подсчитываются значения функции |
f |
|
|
, k 0,n |
, например, с помощью процедуры |
|
|
|
k |
|
|||
метода Гаусса решения систем линейных алгебраических уравнений; |
||||||
- по найденным значениям fk, k 0,n |
|
строится интерполяционный полином Pn x |
||||
Ньютона (Лагранжа); ранее отмечалось, что для рассматриваемого случая многочлен степени n определяется единственным образом; в силу этого построенный полином как раз
ибудет характеристическим.
2.Каким-либо из известных методов решения нелинейных уравнений отыскиваются корни построенного полинома Pn x , которые представляют собой собственные значения
исходной матрицы.
Трехдиагональные матрицы
В практике инженерных расчетов часто встречаются трехдиагональные матрицы, у
которых отличны от нуля лишь коэффициенты, расположенные на главной диагонали, а
также над и под нею. Пусть такая матрица имеет вид
|
a11 |
a12 |
0 |
|
0 |
0 |
0 |
|
|
|
a22 |
a23 |
0 |
0 |
0 |
|
|
|
a21 |
|
||||||
|
0 |
a32 |
a33 |
|
0 |
0 |
0 |
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||
|
0 |
0 |
0 |
|
an 2n 2 |
an 2n 1 |
0 |
|
|
|
0 |
0 |
|
an 1n 2 |
an 1n 1 |
|
|
|
0 |
an 1n |
||||||
|
|
0 |
0 |
|
0 |
ann 1 |
ann |
|
|
0 |
|
|
|||||
Для определения собственных значений требуется подсчитать определитель матрицы
|
a11 |
a12 |
0 |
|
0 |
0 |
0 |
|
|
|
|
a21 |
a22 |
a23 |
|
0 |
0 |
0 |
|
|
|
|
|||||||
|
0 |
a32 |
a33 |
|
0 |
0 |
0 |
|
|
A E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||
|
0 |
0 |
0 |
|
an 2n 2 |
an 2n 1 |
0 |
|
|
|
|
|
0 |
0 |
|
an 1n 2 |
an 1n 1 |
an 1n |
|
|
0 |
|
|||||||
|
|
0 |
0 |
0 |
|
0 |
ann 1 |
|
|
|
|
|
ann |
||||||
132
Разложим этот определитель Dn det A E по коэффициентам нижней строки матрицы A E :
Dn ann Dn 1 ann 1Bnn 1 ,
где |
|
|
|
|
|
|
|
|
|
a11 |
a12 |
0 |
|
0 |
0 |
|
|
|
|
a22 |
a23 |
|
0 |
0 |
|
|
|
a21 |
|
|
|||||
|
0 |
a32 |
a33 |
|
0 |
0 |
|
|
Dn 1 det |
|
|
|
|
|
|
|
, |
|
|
|
|
|||||
|
0 |
0 |
0 |
|
an 2n 2 |
an 2n 1 |
|
|
|
|
0 |
0 |
|
an 1n 2 |
an 1n 1 |
|
|
|
0 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a11 |
a12 |
0 |
|
0 |
0 |
|
|
|
|
|
|
a21 |
a22 |
a23 |
|
0 |
0 |
|
|
|
|
|
|
||||||
|
|
|
0 |
a32 |
a33 |
|
0 |
0 |
|
|
|
Bnn 1 det |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||
|
|
|
0 |
0 |
0 |
|
an 2n 2 |
0 |
|
|
|
|
|
|
|
0 |
0 |
|
an 1n 2 |
|
|
|
|
|
0 |
an 1n |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Этот минор содержит лишь один ненулевой элемент an 1n |
в последнем столбце. В |
|||||||||
этом случае возможно представление |
|
|
|
|
|
|||||
|
|
|
a11 |
a12 |
0 |
|
0 |
|
|
|
|
|
|
|
a21 |
a22 |
a23 |
|
0 |
|
|
|
an 1n |
|
|
|
|
|||||
Bnn 1 |
det |
0 |
a32 |
a33 |
|
0 |
an 1nDn 2 . |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
an 2n 2 |
|
||||
Таким образом, получено рекуррентное соотношение для вычисления значения определителя трехдиагональной матрицы:
Dn ann Dn 1 ann 1an 1nDn 2 .
Для определенности следует положить D 1 0, D0 1. В этом случае, очевидно,
имеют место выражения:
D1 a11 D0 a10a01D 1 a11 ,
D2 a22 D1 a21a12D0 a11 a22 a21a12 ,
... и так далее.
133

Поиск собственных векторов
При численных расчетах, как правило, отыскиваются лишь приближенные величины
собственных значений |
~ |
, |
k 1,n. В этом случае |
|
|
k |
|
|
|||
|
|
|
~ |
|
|
|
|
|
det A kE 0 |
||
и система уравнений |
|
|
|
|
|
|
|
|
~ |
k |
0 |
|
|
|
A kE X |
|
|
позволяет отыскать лишь тривиальное решение Xk 0, k 1,n .
Пусть F Rn - произвольный вектор. Рассмотрим систему уравнений
~ |
(0) |
F . |
(5.5) |
A iE Z |
|
||
Пусть X j, j 1,n - собственные линейно-независимые |
векторы, соответствующие |
||
различным собственным значениям32; эти векторы в |
Rn можно взять в качестве базиса. |
|
Разложим векторы Z(0), F по этому базису: |
|
|
n |
|
n |
Z(0) (j0)X j , |
F |
jX j . |
j 1 |
|
j 1 |
Подставим эти выражения в систему уравнений (5.5):
|
|
|
|
|
|
|
~ |
|
n |
(0) |
X |
j |
|
n |
|
|
|
j |
0, |
|
|
|
|
|
|
|
|
||
|
|
|
|
A iE j |
|
jX |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
(0) |
|
~ |
|
|
j |
|
|
j |
|
|
n |
|
(0) |
AX |
j |
~ |
j |
jX |
j |
|
|
|
|
|||||
j |
|
A iE X |
|
jX |
|
j |
|
|
i |
X |
|
|
|
|
|||||||||||||||
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
(0) |
|
j |
~ |
|
X |
j |
jX |
j |
|
|
n |
|
|
(0) |
|
~ |
|
|
j |
0. |
|
|
|
|||
j jX |
|
i |
|
|
j j i j X |
|
|
|
|
||||||||||||||||||||
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В силу линейной независимости векторов X j, |
|
j 1,n |
получаем |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
(0) |
|
|
~ |
|
|
|
|
|
|
|
|
(0) |
|
|
|
j |
~ |
, |
j 1,n . |
|
|
|
|
|
|
|
|
|
j |
j i j 0, |
|
j |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j i |
|
|
|
|
|
|
|
|
|||
При условии, что |
|
i |
~ |
|
, коэффициент |
|
(0) |
|
|
|
|
|
|
|
|
|
(0) |
(0) |
, |
k i, |
|||||||||
|
i |
i |
|
становится большим, i |
k |
||||||||||||||||||||||||
вследствие чего |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z(0) |
|
(j0)X j (i |
0)Xi , |
|
|
|
|
|
|
|
|
||||||||||||
j 1
32 Согласно [7], собственные векторы, соответствующие попарно различным собственным значениям, линейно независимы.
134

то есть вектор Z(0) будет близок по направлению к собственному вектору Xi . Повторим решение системы уравнений (5.5) с новой правой частью:
~ |
(1) |
Z |
(0) |
. |
A iE Z |
|
|
Вновь представим решение в виде разложения
n
Z(1) (j1)X j j 1
иповторим предыдущие рассуждения, что приведет к выражению
(0)
j , j 1,n.~(j1)
|
j |
i |
|
|
Очевидно, что поскольку величина |
i(0) значительно преобладает над остальными |
|||
коэффициентами (j0), |
j i, новый коэффициент |
(i1) будет еще больше, чем (i |
0) , то есть |
|
вектор Z(1) будет еще ближе по направлению к собственному вектору Xi . Иными словами возможно построение итерационного процесса вида
~ |
(k 1) |
Z |
(k) |
, |
(5.6) |
A iE Z |
|
|
причем Z(0) - произвольный начальный вектор.
Следует отметить, что если собственное значение вычислено достаточно точно, то
~ |
|
|
det A iE 0, что может привести к аварийной остановке вычислительного процесса. |
||
В этом случае для повышения устойчивости расчетов в матрицу |
~ |
вносится |
A iE |
||
|
~ |
|
некоторая погрешность, например, за счет искажения собственного значения i . |
|
|
1 |
2 |
|
Пример 5.4. Определить собственные векторы для матрицы A |
. |
|
5 |
4 |
|
При выполнении примера 5.1 получены собственные значения 1 6, 2 1. Для
определения собственных векторов, соответствующих первому собственному значению,
~
зададим погрешность e : 1 1 6 .
Система уравнений (5.6) для первого вектора Z(0) |
1 |
|||||||
принимает вид |
||||||||
|
|
|
|
|
|
|
|
1 |
5 X |
11 2X12 1, |
|
||||||
|
5X1 |
|
|
2 |
|
X1 1. |
|
|
|
|
|||||||
|
1 |
|
|
|
2 |
|
||
Это система уравнений имеет следующее решение: |
|
|||||||
|
4 |
|
|
|
|
10 |
||
X11 |
7 |
, |
X12 7 . |
|||||
135
Для погрешности e=0,001 получаем |
|
X11 5714897872,, |
X12 1428510213,, |
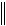 X1
X1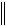 1538584416,.
1538584416,.
После нормирования компоненты собственного вектора единичной длины
X11 0371438695,, |
X12 0928457482,. |
Первый собственный вектор, определенный ранее для этой же матрицы,
X |
1 |
1 |
2 |
0371390676, |
|
|
|
|
|
. |
|
|
|
29 |
5 |
0928476691, |
|
Выполним такую же процедуру для второго собственного значения:
~ |
2 |
1; |
2 |
||
2 X |
12 2X22 1, |
|
|
|
|
|
|
|
|
2 |
2 |
5X |
1 5 X2 1; |
|
|
|
|
|
|
15 9 |
|
3 |
|
|
|
X12 |
5 7 , |
X |
22 7 ; |
|
|
|
X12 |
428767319,, |
X22 |
4286530496,; |
||
|
|
|
|
|
X2 6062877623,. |
||
Нормированный собственный вектор |
|
|
|||||
|
|
X12 0707201012,, |
X22 0707012538,. |
||||
Второй собственный вектор, определенный в примере 5.1, отличается от найденного |
|||||||
лишь направлением: X |
2 |
2 1 |
0707106781, |
||||
|
|
|
|
|
|
. |
|
|
|
2 |
1 |
|
0707106781, |
||
Частичная проблема собственных значений
Часто возникает задача определения не всего спектра собственных значений и векторов, а лишь каких-то, например, максимального и минимального собственных значений и соответствующих им векторов. В этом разделе рассматриваются простейшие способы вычисления собственных чисел и векторов. Для более широкого знакомства с проблемой собственных значений можно дополнительно обратиться к монографиям [11, 12].
Метод линеаризации
136

Пусть рассматривается задача (5.1), которую представим в компонентной форме
n |
|
|
fi X, aijXj Xi, |
i 1,n . |
(5.7) |
j 1
Полученное выражение можно рассматривать как систему n нелинейных уравнений с (n+1) неизвестными величинами , Xk , k 1,n . Для замыкания системы уравнений можно добавить условие нормирования собственного вектора:
n |
|
|
X 2 Xj 2 |
1. |
(5.8) |
j 1
Использование метода Ньютона для решения системы нелинейных уравнений (5.7) - (5.8) приводит к итерационному процессу
fi X |
(k), (k) fi X |
(k) |
|
(k) |
DX(jk) 0, |
i 1,n , |
|
||||
|
, |
|
|||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
j 1 |
|
Xj |
|
|
|
|
|||
|
|
2 |
|
n |
X(k) |
2 |
DX(jk) 0, |
|
|
||
|
X(k) |
|
|
|
|
Xj |
|
|
|
||
|
|
|
|
j 1 |
|
|
|
|
|
||
где DX(jk) X(jk 1) X(jk) . |
|
|
|
|
|
|
|
|
|
|
|
Учитывая конкретный вид уравнений (5.7) и (5.8), получаем |
|
||||||||||
n |
|
|
(k) DX(ik) |
n |
|
i 1,n; |
|||||
aijDX(jk) D(k) X(ik) |
aijX(jk) (k)X(ik), |
||||||||||
j 1 |
|
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.9) |
|
|
|
|
|
|
|
|
|
|
|
|
n |
n |
|
|
2 |
|
|
|
|
|
|
|
2 X(jk)DX(jk) 1 X(jk) . |
|
|
|
|
|
|
|||||
k 1 |
j 1 |
|
|
|
|
|
|
|
|
|
|
В результате такого итерационного процесса будет найдено какое-то собственное значение и соответствующий ему собственный вектор, в зависимости от начального приближения.
Пример 5.5. Определить методом линеаризации собственные векторы матрицы
1 |
2 |
A |
. |
5 |
4 |
Согласно формулам (5.9) получаем итерационную процедуру для вычисления собственных значений и векторов:
137

|
(k) |
|
(k) |
|
|
(k) |
|
(k) |
|
|
|
(k) |
|
|
|
|
|
(k) |
|
|
(k) |
|
(k) |
(k) |
(k) |
; |
|
||||||
1 DX1 |
2 DX2 |
X1 |
D |
|
|
|
|
|
DX1 |
|
|
|
X1 |
1 X1 2 X2 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(k) |
|
(k) |
|
|
(k) |
|
(k) |
|
|
(k) |
|
|
|
|
|
(k) |
|
|
|
(k) |
|
(k) |
(k) |
4 X |
(k) |
; |
||||||
5 DX1 |
4 DX2 |
X2 |
D |
|
|
|
|
|
|
DX2 |
|
|
X2 |
5 X1 |
2 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2X(k)DX(k) |
1 |
|
X(k) |
|
2 |
|
|
X(k) |
|
2; |
|
|
|
|
|
|
|
|
|
|||||||||||
2X(k)DX(k) |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
1 |
1 |
2 |
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||
1 (k) DX1(k) |
2 DX2(k) |
X1(k) D (k) |
(k) X1(k) |
1 X1(k) 2 X2(k); |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(k) |
|
(k) |
|
(k) |
|
|
|
|
(k) |
|
|
|
|
|
(k) |
|
|
|
(k) |
|
(k) |
|
(k) |
(k) |
|
|
|
||||
5 DX1 |
4 |
|
DX2 |
X2 |
D |
|
|
|
X2 |
5 X1 4 X2 ; |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(k)DX |
(k) 1 |
|
X(k) |
|
2 |
|
|
X(k) |
|
2. |
|
|
|
|
|
|
|
|||||||||||
2X(k)DX(k) 2X |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
1 |
|
1 |
|
2 |
|
2 |
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||
На каждом этапе расчетов очередное приближение решения определяется по формулам
X1(k 1) X1(k) DX1(k), |
X2(k 1) X(2k) DX2(k), |
(k 1) (k) D (k) . |
Результаты расчетов сведены в табл. 5.2.
Таблица 5.2
Расчет собственного значения и вектора методом линеаризации
Номер |
X1(k) |
X(2k) |
|
итерации |
|
|
|
|
|
|
|
0 |
1,0 |
1,0 |
1,0 |
1 |
-0,375 |
1,875 |
4,75 |
2 |
0,45741931 |
1,082795321 |
6,26862705 |
3 |
0,376979184 |
0,946529203 |
6,038835844 |
4 |
0,371426686 |
0,928555837 |
6,000515885 |
5 |
0,371390677 |
0,928476699 |
6,000000051 |
6 |
0,371390676 |
0,928476691 |
6,000000000 |
|
|
|
|
|
|
Очевидно, |
что |
решение сошлось к найденным |
ранее собственному вектору |
||
X |
1 |
1 |
2 |
|
0371390676, |
6. |
|
|
|
|
|
и собственному значению 1 |
|||
|
|
29 |
5 |
|
0928476691, |
|
|
Степенной метод
Степенной метод предназначен для определения наибольшего (по модулю)
собственного значения.
Пусть все собственные числа упорядочены следующим образом:
 1
1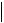
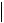 1
1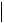
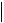 n
n .
.
Рассмотрим итерационный процесс вида
138
