Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пермский национальный исследовательский политехнический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Boyarshinov_ChM_T1

.pdf

Скачиваний:

132

Добавлен:

13.03.2016

Размер:

1.32 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1811 12 13 14 15 16 17 18 > Следующая >>>

a,b

y x

x ,

Очевидно, что в узлах

xk ,

k 0,n

погрешность

r xk 0.

Для

оценки

погрешности

выберем

зафиксируем

произвольную

точку

x a,b ,

x xk ,

0,n. Рассмотрим вспомогательную функцию

n ,

x x

(4.6)

g s

y s

s Kw

s , s a,b ,

x x

K - константа. Очевидно, что g xk 0, k 0,n. Выберем константу К в выражении (4.6)

так, чтобы для выбранного значения x функция g(x) = 0, то есть

y x Pn x

w x

Пусть функция

y(x) имеет (n+1) производную, то есть является достаточно гладкой

функцией. Согласно построению функция

g(s)

имеет не менее

(n+2)

нулей в точках

x, x0, , xn . В этом случае функция

g s

на отрезке [a,b] имеет не менее (n+1)

нулей;

g s - не менее n

нулей, и так далее. И,

наконец,

g(n 1) s

имеет хотя бы один корень на

отрезке [a,b]. Иначе говоря, a,b ,

g(n 1) 0. В силу определения функции g(s),

g(n 1) s y(n 1) s K n 1 !,

и для точки получаем

y n 1 K n 1 ! n 1 !y x Pn x .

w x

Отсюда следует

y(n 1)

y x Pn x

(n 1)!

x .

Окончательно,

y x P

Mn 1 x ,

sup y(n 1) x

(4.7)

(n 1)!

n 1

x a,b

В частном случае, когда y(x) является полиномом степени n, Mn 1 0

и y x Pn x .

Дополнительно можно подобрать такое распределение узловых точек xk ,

k 0,n,

чтобы

минимизировать выражение

x x x0 x x1 x xn 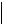1 xn 1 anxn an 1xn 1 a0,

являющееся полиномом степени n со старшим коэффициентом, равным 1. Иначе говоря,

получена задача Чебышёва, рассмотренная ранее. Искомый полином имеет на отрезке [a,b]

корни

xk	b a	b a cos	2k	1	p,	k 0,n .
	2	2	2 n	1

Оценка модуля полинома, наименее уклоняющего от нуля,

max x	b a n 1 .
	2	2n 1
x a,b

Оценка погрешности полинома Ньютона (Лагранжа) при использовании узловых точек, соответствующих корням полинома Чебышева, имеет вид

y Pn maxy x Pn x		Mn 1	b a n 1
		(n 1)! 2		2n 1 .

x a,b
Сходимость интерполяционного процесса
Множество точек a x0 x1	xn b	назовем сеткой на отрезке [a, b] и
обозначим n . Рассмотрим последовательность сеток			0, 1, 2, , n , Построим на

отрезке [a,b] последовательность полиномов Pn x , аппроксимирующих с помощью сеток
n	функцию y(x).
	Интерполяционный процесс сходится в точке x* a,b , если существует предел
lim P		x*	y x*	(определение поточечной сходимости).
n	n
	Интерполяционный процесс сходится равномерно на отрезке [a, b], если

y P	maxy x	P x	0	.
n		n	n	.

	x a,b

Теорема 4.1 (Фабера26). Какова бы ни была последовательность сеток n , найдется непрерывная на [a,b] функция y(x) такая, что последовательность интерполяционных полиномов Pn x не сходится к y(x) равномерно на этом отрезке.

На рис. 4.1 приведен пример аппроксимации непрерывной функции f(x) = |x| на последовательности сеток с равноотстоящими узлами.

26 Фабер Георг [5.4.1877 - 1966] - немецкий математик, был профессором Высшей технической школы в

Мюнхене с 1916 года

100

1.4
1.2
1
0.8
0.6
0.4
0.2
0
-1	-0.8	-0.6	-0.4	-0.2	0	0.2	0.4	0.6	0.8	1
Рис. 4.1. Аппроксимация на отрезке [-1, 1] функции f(x) = \|x\| полиномами Pn, построенными
			с использованием равномерных сеток

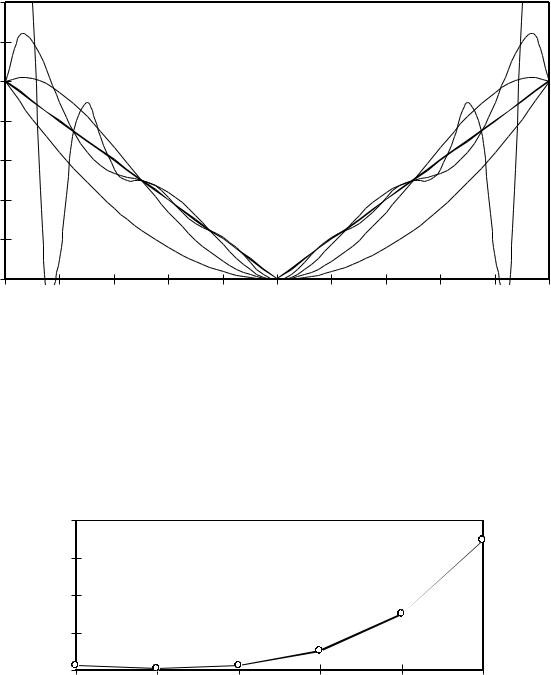
На рис. 4.2 представлен график погрешности аппроксимации функции f(x) = |x|

полиномамм на равномерных сетках в зависимости от числа отрезков сеточной области.

\|\|f-Pn\|\|
1E+15
1E+11
1E+07
1000
0.1
2	4	8	16	32	64	n
Рис. 4.2. Погрешность аппроксимация на отрезке [-1, 1] функции f(x) = \|x\|						в
	зависимости от числа отрезков равномерной сетки.

Теорема 4.2. Если функция y(x) непрерывна на отрезке [a,b], то найдется такая последовательность сеток, для которой интерполяционный процесс сходится равномерно на этом отрезке.

На рис. 4.3 приведен пример аппроксимации непрерывной функции f(x) = |x| на последовательности неравномерных (чебышевских) сеток. На рис. 4.4 представлен график

101

погрешности аппроксимации функции f(x) = \|x\| полиномом Pn								на чебышевской сетке в
зависимости от числа отрезков сеточной области.
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
-1	-0.8	-0.6	-0.4	-0.2	0	0.2	0.4	0.6	0.8	1
Рис. 4.3. Аппроксимация на отрезке [-1, 1] функции f(x) = \|x\| полиномами Pn, построенными
			с использованием чебышёвских сеток

Интерполяционный многочлен Эрмита27

Пусть заданы значения yk функции и некоторых ее производных в точках xk , k 0,n

отрезка [a,b]. Если потребовать от полинома Pn x совпадения не только значений функции

(4.1), но и значений производных в заданных точках, то интерполяция носит название

эрмитовой, а сам полином обозначается как Hp x .

Построим полином Pn x согласно процедуре Ньютона. Далее начнем сближать,

например, узлы x0 и x1 , которые в пределе совпадут, то есть появится кратный узел x0 x1

, что делает невозможным подсчет разделенной разности,

y x0,x1 y x0 y x1 . x0 x1

Однако с помощью предельного перехода можно установить, что

lim y x0,x1	lim y x0 y x1 y x1 .
x0 x1	x0	x1	x0	x1

27 Эрмит Шарль [24.12.1822 - 14.1.1901] - французский математик. С 1856 года являлся членом Парижской академии наук, с 1857 года - иностранным членом-корреспондентом Петербургской академии наук. С 1869

года был профессором Парижского университета. С 1873 года стал членом Лондонского королевского общества. С 1895 года избран иностранным почетным членом Петербургской академии наук.

102

\|\|f-Pn\|\|
0.25
0.2
0.15
0.1
0.05
0
2	4	8	16	32	64	n
Рис. 4.4. Погрешность аппроксимация функции f(x) = \|x\| на отрезке [-1, 1]						в
	зависимости от числа отрезков чебышёвской сетки.

Иными словами, первая разделенная разность, что уже отмечалось ранее, совпадает со значением первой производной в точке x0 . Это будет означать также, что полином Эрмита

Hp x позволяет правильно передавать значения производных.

Разделенные разности более высоких порядков определяются с учетом этого следующим образом:

y x0,x0,x1 y x0 y x0,x1 , x0 x1

y x	0,x0	,x1 y x0	,x1,x1	y x0	2y x0,x1 y x1
y x0,x0,x1,x1		x0 x1			x0 x1	.
		x0 x1			x0 x1

Отсюда следует, что слияние трех узлов дает возможность интерполяции значений вторых производных, и так далее.

В общем случае имеет место формула:

					1	y(m 1) x	0 .
y x0		, x0	, ,x	0	1	y(m 1) x	0 .
	1442443				m 1 !
			m

Оценку точности аппроксимации выполним с ипользованием формулы (4.7):

y x Hn x	Mn 1	~
y x Hn x	n 1 !	w x ,
	n 1 !

p			p
~	mk	,	mk n 1,
w x x xk		,	mk n 1,
k 0			k 0

где p - число точек интерполяции, mk - число значений функции и ее производных в точке

xk . Такой выбор функции w x обеспечивает обращение в нуль не только g(s), но и ее

производных gmk xk .

103

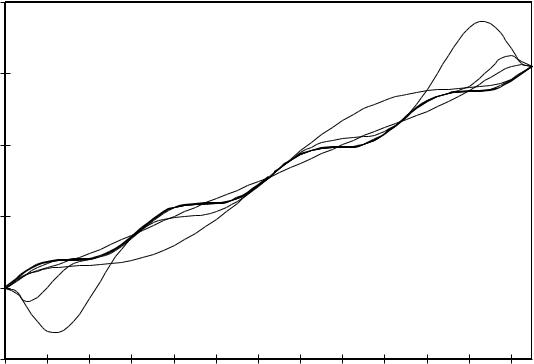
На рис. 4.5 приведены приближения функции								f x x sin x полиномами Эрмита
H3(x), H5(x), H7(x), H9(x) (на рисунке аппроксимация H9(x) практически совпадает с самой
функций) и полиномом Лагранжа P9(x) для отрезка								[0, 25]	на равномерных сеточных
множествах.
32
24
16
8
0
-8
0	2	4	6	8	10	12	14	16	18	20	22	24
	Рис. 4.5. Графики интерполяционных полиномов Эрмита и Лагранжа

104

Интерполяция сплайнами

Сплайн - способ аппроксимации функции, заданной таблично, с помощью набора кусочно-полиномиальных зависимостей. Исторически понятие сплайна28 связывают с гибкой линейкой, применяемой в чертежных работах. Из курса механики деформируемых стержней известно уравнение изгиба упругого стержня:

EIuiv q x ,

где Е - модуль упругости, I - момент инерции поперечного сечения, u - функция прогиба, q(x) - распределенная нагрузка. В случае отсутствия нагрузки получаем однородное уравнение

uiv 0,

имеющее решение, представляемое кубическим полиномом

u С0 С1x С2x2 С3x3 ,

Ci - постоянные интегрирования, определяемые из граничных условий. Иными словами,

гибкая линейка, помещенная на плоскости, плавно (то есть без изломов) изогнется так, что ее форму между любыми двумя соседними точками можно описать кубической параболой.

Поэтому традиционно под сплайном понимают интерполяцию табличной функции с помощью отрезков кубического полинома.

Построение кубического сплайна
Пусть на отрезке				[a,b] задана		сетка	a x0 x1 xn b;	известны	табличные
значения функции	f	x	,	k 0,n	в узлах этой сетки.
значения функции			k		в узлах этой сетки.
Потребуем, чтобы сплайн S(x) удовлетворял следующим условиям:
а) на каждом сегменте xk 1,xk ,						k 1,n	являлся полиномом третьей степени;
б) был непрерывен вместе с первой S x							и второй S x производными на [a,b];
в) совпадал со значениями аппроксимируемой функции в узлах сетки.
Сплайн S(x) на каждом сегменте xk 1,xk отрезка a,b строится в виде
	Sk x ak bk x xk ck x xk 2 dk x xk 3,							k 1,n ;	(4.8)
						2	6

Первые и вторые производные:

28 spline (англ.) - гибкая линейка.

106

Sk x bk ck x xk dk x xk 2 , 2

Sk x ck dk x xk ,

двух “соседних” сплайнов Sk(x) и Sk+1(x) в общей точке должны удовлетворять условию б),

откуда получаем систему уравнений (условия непрерывности сплайна и его производных):

k 1

ck 1

dk 1

, k 1,n 1,

k 1

dk 1

k 1

k 1,n 1,

k 1

k 1,n 1

k 1

И, наконец, условия в) дают выражения

k 1,n .

Обозначим

hk 1

xk 1

длины отрезков.

Теперь предыдущие выражения можно

записать в виде системы алгебраических уравнений относительно неизвестных

коэффициентов ak ,bk,ck ,dk,

k 1,n :

ck 1

2 dk 1 h

3, k 1,n 1,

(4.9)

k 1

dk 1

k 1,n 1,

(4.10)

k 1

k 1 k 1

k 1

ck ck 1

dk 1hk 1,

k 1,n 1,

(4.11)

1,n

(4.12)

Система (4.9) - (4.12) содержит ( 4n - 3) уравнения с (4n) неизвестными. Учтем

дополнительно, что для точки

x0 a

имеет место соотношение

S1 x0 a1 b1 x0 x1 c1 x0 xk 2 d1 x0 xk 3 f x0 .

Используя соотношения (4.12), в последнем выражении и уравнениях (4.9) можно исключить “лишние” неизвестные ak, k 1,n , а сами уравнения записать в форме

ck 1 h

2 dk 1 h

, k 0,n 1.

(4.13)

k 1

В результате система (3n-2) уравнений (4.10), (4.11) и (4.13) содержит 3n неизвестных

bk,ck,dk, k 1,n .
Для “замыкания“ этой системы уравнений положим
S a 0,	(4.14)

107

S b 0,

(4.15)

что соответствует “нулевым” кривизнам в начальной и конечной точках, то есть

“свободным” концам сплайна. Возможны и иные условия для замыкания системы уравнений, например, указание значения производной (наклона касательной) в конечной или начальной точках, и некоторые другие.

Условие (4.14) с помощью выражения (4.8) удобно представить в форме

S1 x0 c1 d1h1 0,

а формулу (4.15) - в виде

Sn xn cn 0,

что позволяет переписать уравнения (4.11)

dkhk ck ck 1,

k 1,n;

c0 0;

cn 0.

(4.16)

В итоге получена система (3n+1) уравнений (4.10), (4.13), (4.16), содержащих (3n+1)

неизвестную величину.

Рассмотрим два уравнения вида (4.13)

fk ,

bkhk

k hk

bk 1hk 1 ck 1 hk 12 dk 1 hk 13 fk 1 fk ,

k hk

k 1

k hk

fk 1 fk ck 1 h

dk 1 h

k 1

Подставим полученные выражения для

bk , bk 1

в уравнения (4.10) :

dk 1 h

k 1

f xk 1 f xk

k 1 h

xk f xk 1

k h

hk 1

k 1

ck 1hk 1 ckhk

dkhk

f xk 1 f xk

f xk f xk 1

k 1,n 1.

dk 1hk 1

hk 1

Формулы (4.16) позволяют получить выражения

dkh2k ck ck 1 hk ,

dk 1h2k 1 ck 1

ck hk 1 ,

благодаря чему предыдущая формула преобразуется к виду:

108

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1811 12 13 14 15 16 17 18 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
19.07.201978.85 Кб2bilety_43-49.doc
#
13.03.2016105.07 Кб48bilety_fkhma (1).docx
#
22.09.2019260.61 Кб2bilety_po_istorii1_1.doc
#
29.03.2015539.41 Кб6bilety_sgmu.docx
#
29.03.2015545.25 Кб5bilety_sgmu.docx
#
13.03.20161.32 Mб132Boyarshinov_ChM_T1.pdf
#
13.03.20162.93 Mб308Boyarshinov_ChM_T2.pdf
#
13.03.20161.69 Mб99Boyarshinov_ChM_T3.pdf
#
21.08.201955.81 Кб6British Etiquette and Manners.doc
#
01.05.2019559.62 Кб4budget.doc
#
29.03.20153.3 Mб25buhgal.pdf