Boyarshinov_ChM_T1

Контрольные вопросы и задания

Какие методы решения системы линейных алгебраических уравнений называются

прямыми и итерационными?

Сформулируйте условия существования и единственности решения системы

линейных алгебраических уравнений.

Сформулируйте условия разрешимости системы линейных алгебраических

треугольными матрицами.

Как можно вычислить определитель матрицы коэффициентов, используя процедуру метода Гаусса?

Обоснуйте возможность построения обратной матрицы с помощью решения системы линейных алгебраических уравнений.

Выбор "главного" элемента при использовании метода Гаусса возможен с помощью перестановки либо строк, либо столбцов. Обоснуйте, какой вариант предпочтителен.

Сформулируйте условия применимости метода "квадратного корня" для решения системы линейных алгебраических уравнений.

Сравните методы Гаусса и квадратного корня для решения системы линейных алгебраических уравнений. Укажите достоинства и недостатки каждого из этих методов.

Сформулируйте понятие устойчивости системы линейных алгебраических уравнений.

71

Чему равно и что характеризует число обусловленности системы линейных алгебраических уравнений?

оценивать при выполнении вычислений на ЭВМ?

Приведите классификацию итерационных методов решения системы линейных алгебраических уравнений. Какие критерии можно использовать для остановки итерационного процесса?

Укажите геометрический смысл сходимости (расходимости) решения системы алгебраических уравнений при использовании итерационных методов.

Дайте определение понятия скорости сходимости итерационного процесса.

Обоснуйте идею и поясните условия применимости метода Якоби.

Обоснуйте идею и поясните условия применимости метода Зейделя.

Покажите, что из условия B - 0,5 A > 0 теоремы 2.4 следует существование обратной матрицы B-1.

Докажите справедливость неравенства (Dx, x) > 0, использованного при доказательстве следствия 1 из теоремы 2.4.

Укажите условия применимости метода верхней релаксации.

Сформулируйте условия сходимости стационарного итерационного метода.

Сформулируйте задачу, решение которой приводит к построению полинома Чебышева на отрезках [-1, 1] и [a, b].

Вчем преимущество метода решения системы линейных алгебраических уравнений

счебышевским набором параметров?

Опишите порядок выбора итерационных параметров в методе минимальных невязок.

Опишите порядок выбора итерационных параметров в методе минимальных поправок.

Опишите порядок выбора итерационных параметров в явном методе скорейшего спуска.

Опишите порядок выбора итерационных параметров в неявном методе скорейшего спуска.

72

3 . Н Е Л И Н Е Й Н Ы Е У Р А В Н Е Н И Я

Пусть известна некоторая нелинейная зависимость вида y= f(x). Требуется определить все те значения аргумента ~xk , k 1,2, , которые обращают функцию в нуль:

Для поиска корней нелинейных уравнений, как правило (за небольшим исключением:

квадратные, кубические, некоторые трансцендентные уравнения) используются итерационные методы.

Первоначально рассматриваются методы решения одного нелинейного уравнения, а

затем - системы нелинейных уравнений.

Методы вычисления корней нелинейного уравнения16

Метод половинного деления17

Метод основан на одной из теорем математического анализа. Согласно [10], функция,

непрерывная в замкнутом интервале и принимающая на концах этого интервала значения разных знаков, хотя бы один раз обращается в нуль внутри интервала.

Пусть функция f(x) непрерывна на отрезке x0, x1 . Процедура метода заключается в последовательном сокращении длины отрезка для локализации корня уравнения (3.1).

Первоначально проверяются значения заданной функции на концах отрезка. В случае, если

f x0 f x1 0,

один из концов отрезка является искомым корнем уравнения.

Пусть на концах отрезка значения функции имеют разные знаки, то есть имеет место соотношение

f x0 f x1 0.

16Дополнительно методы решения нелинейных уравнений рассматриваются в разделе, посвященном интерполяции функций.

17Встречаются иные названия этого метода - метод бисекции, дихотомии.

73

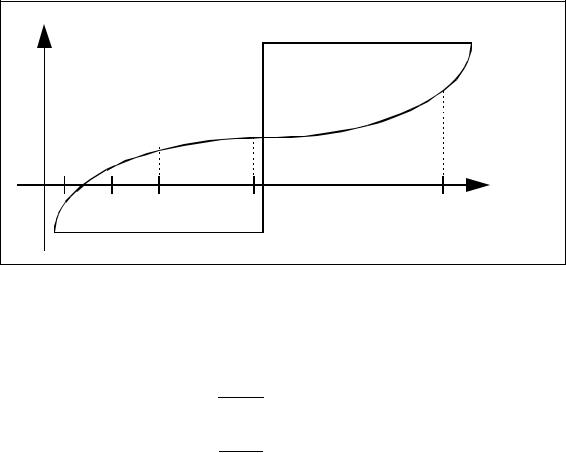
Если имеет место соотношение f x0 f x2 0 (рис. 3.1), то корень следует искать на отрезке x0, x2 . В противном случае - корень разыскивается на отрезке x2, x1 . В

результате выполненной операции исходный отрезок сократился вдвое.

Далее, в зависимости от ситуации, отрезок вновь делится пополам,

и так далее.

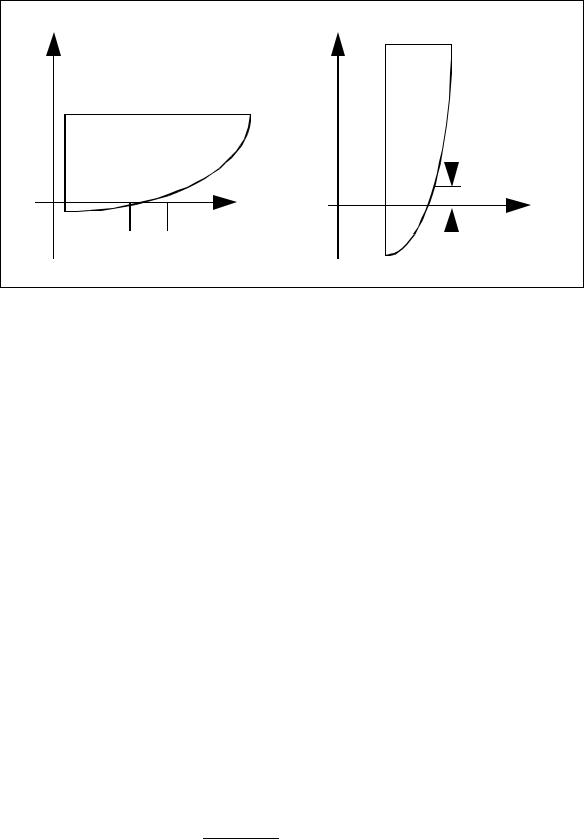
Для прекращения вычислительной процедуры применяются различные критерии: - если функция достаточно “пологая”, имеет смысл использовать условие (рис.3.2a)

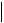xk 1 xk x ;

- если функция “круто” меняет свое значение, целесообразно применять условие

(рис.3.2b)

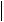yk 1 y .

74

то уравнение (3.2) имеет на отрезке А единственное решение ~x , метод простой итерации

Доказательство.

Докажем “по индукции”, что определяемые в соответствии с формулой (3.2) величины x(n) A n.

x(0) A по условию теоремы.

Пусть x(n) A; покажем, что и x(n 1) A .

В силу x(n 1) x(n) имеем

x(n 1) a x(n) a x(n) a a a x(n) a a a ,

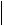x(n 1) a 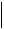x(n) a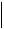 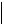a a C x(n) a 1 C r C r 1 C r r,

то есть x(n 1) A .

Теперь оценим разность получаемых решений для произвольного n:

x(n 1) x(n) 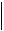x(n) x(n 1) 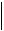C x(n) x(n 1).

Отсюда получаем

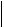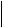x(n 1) x(n) C x(n) x(n 1) C2 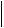x(n 1) x(n 2) 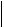Cn 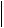x(1) x(0).

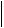Для двух произвольных значений x(p), x(q) (для определенности положим p > q) на основании этого соотношения имеем

18Липшиц Рудольф Отто Сигизмунд [14.5.1832 - 7.10.1903] - немецкий математик. С 1864 года является профессором Боннского университета. В 1900 году избран членом - корреспондентом Парижской академии наук.

77

x(p) x(q) x(p) x(p 1) x(p 1) x(q) x(p) x(p 1) x(p 1) x(p 2) x(p 2) x(q)

p1

x(k 1) x(k) ,

Очевидно, что при p,q имеет место

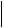x(p) x(q) 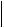0,

и в соответствии с признаком Больцано - Коши19

Переходя к пределу в соотношении x(n 1) x(n) , в силу непрерывности функции

x получаем:

x* lim x(n 1) lim x(n) x* ,

n n

то есть x* ~x - решение уравнения (3.2).

19Больцано Бернард [5.10.1781 - 18.12.1848] - чешский математик, философ, теолог. В 1800 году закончил философский, а в 1805 - теологический факультеты Пражского университета. В этом же университете с 1805

года возглавлял кафедру истории религии, откуда был уволен в 1820 году за вольнодумство и лишен права публичных выступлений. После этого занимался исследованием в области логики и математики.

Коши Огюстен Луи [21.8.1789 - 23.5.1857] - французский математик. В 1807 году окончил Политехническую школу, в 1810 году - Школу мостов и дорог в Париже. С 1810 по 1813 годы работал инженером в Шербурге.

С 1816 года был избран членом Парижской академии наук. С 1816 по 1830 год преподавал в Политехнической школе и в Коллеж де Франс. С 1831 года стал иностранным почетным членом Петербургской академии наук. В 1848 году начал преподавать в Парижском университете.

Признак сходимости числовой последовательности Больцано-Коши [8]: для того, чтобы последовательность вещественных чисел имела конечный предел, необходимо и достаточно, чтобы x(p) x(q) 0 при

p,q .

78

Теперь покажем, что получаемое решение единственно. В самом деле, пусть

что может иметь место при условии 0 < C < 1 лишь в случае x* x** .

Оценим погрешность метода простой итерации после выполнения N итераций:

Что и требовалось доказать.

Следствие 1. Если 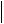x C 1 x A , а также имеет место соотношение

то уравнение (3.2) имеет единственное решение, метод простых итераций сходится и имеет место оценка (3.5).

Действительно, согласно теореме Лагранжа20,

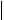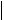
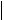
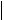(b) (a) b a b a max b a ,

x A

то есть в качестве константы условия Липшица можно принять

C max x .

x A

В этом случае условия теоремы (3.1) выполняются и все ее утверждения имеют место.

20 Лагранж Жозеф Луи [25.11.1736 - 10.4.1813] - французский математик и механик. В 1755 году стал профессором Туринской артиллерийской школы. В 1759 годубыл избран членом Берлинской академии наук.

С 1766 года был директором Математического класса Берлинской академии наук, с 1772 года - членом Парижской академии наук, с 1776 года - иностранным почетным членом Петербургской академии наук. В 1795 году стал профессором Парижской Нормальной школы, с 1797 года - профессором Политехнической школы.

Теорема Лагранжа [10]: если функция f(x) непрерывна в замкнутом интервале a, b и дифференцируема во

всех его внутренних точках, то внутри этого интервала существует хотя бы одна точка , для которой

f(b) f(a) f ( ). b a

79

которое с учетом

f ~x 0

позволяет получить выражение

~x x f x , f x

приводящее к итерационному процессу следующего вида:

Очевидно, что метод Ньютона можно рассматривать как вариант метода простых

f x

итераций, при условии x x f x .

Геометрическая иллюстрация итерационного процесса метода Ньютона приведена на рис. 3.4, из которого понятно, что каждое следующее приближение может быть определено из геометрических построений:

80