
Boyarshinov_ChM_T1
.pdf
Итерационные методы решения
Итерационными называются методы, при которых решение системы уравнений (2.1)
получается как предел некоторой последовательности.
Вновь рассмотрим систему линейных алгебраических уравнений с отличным от нуля определителем det(A), которую представим в компонентной форме
m |
|
|
ai jxj |
fi, |
i 1,m . |
j 1 |
|
|
Преобразуем эту систему к виду
|
|
|
i 1 |
|
m |
|
|
|
|
|
aijxj aiixi |
aijxj |
fi , |
||||
|
|
|
j 1 |
|
j i 1 |
|
|
|
|
1 |
|
i 1 |
m |
|
|
|
|
xi |
aijxj |
aijxj |
|
i 1,m. |
||||
|
|
fi |
, |
|||||
|
a |
ii |
|
|
|
|
|
|
|
|
|
j 1 |
j i 1 |
|
|
|
|
Метод Якоби9
Последнее выражение представим в виде итерационной схемы
(n 1) |
|
1 |
|
i 1 |
m |
|
|
|
|
(n) |
(n) |
i 1,m , |
(2.9) |
||||
xi |
|
fi |
ai jxj |
ai jxj |
, |
|||
|
|
ai i |
j 1 |
j i 1 |
|
|
|
|
где n - номер итерации. Для получения решения используется следующий алгоритм. В
качестве нулевого приближения выбираются какие-либо (зачастую произвольные) значения x(j0), j 1,m искомых величин, которые подставляются в правую часть выражения (2.9), что позволяет определить первое приближение неизвестных x(j1), j 1,m. Затем полученный результат вновь подставляется в правую часть выражения (2.9) и вычисляются x(j2), j 1,m,
и так далее. Вычислительный процесс заканчивается, например, когда выполняется условие
max x(jn 1) x(jn)
x(jn 1) x(jn) , 1 j m
, 1 j m
где e > 0 - заданная точность вычисления результата.
Пример 2.3. Рассмотрим систему алгебраических уравнений
9 Якоби Карл Густав Якоб [10.2.1804 - 18.2.1851] - немецкий математик. С 1830 года являлся иностранным членом-корреспондентом (с 1833 года - иностранным почетным членом) Петербургской академии наук; с 1836 года - членом Берлинской академии наук; с1846 года - членом Парижской академии наук; с 1833 года -
членом Лондонского королевского общества. С 1829 по 1942 годы был профессором Кенигсбергского университета.
42

4x 2y 5,
3x 5y 9.
Точное решение этой системы x = 0,5, |
y=1,5 . |
|
|||
Из первого уравнения выразим первую неизвестную x |
|||||
|
x 5 2y |
, |
|
||
|
|
|
4 |
|
|
а из второго - неизвестную y, |
|
|
|
|
|
|
y 9 3x . |
|
|||
|
|
|
5 |
|
|
Представим полученные выражения в виде итерационной схемы |
|||||
|
(n 1) |
|
5 2y(n) |
||
x |
|
4 |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(n) |
|
9 3x . |
||||
y(n 1) |
|||||
|
|
|
5 |
|
|
|
|
|
|
|
|
В качестве начального приближения примем x(0) 0, y(0) 0. Результаты расчетов
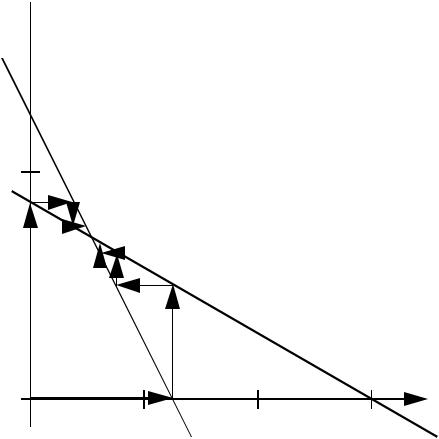
сведены в табл. 2.1. На рис. 2.1 графически показан ход выполнения итерационного процесса метода Якоби.
Таблица 2.1
Результаты выполнения итерационной процедуры метода Якоби
n |
x(n) |
y(n) |
|
|
|
0 |
0 |
0 |
1 |
1,25 |
1,8 |
2 |
0,35 |
1,05 |
3 |
0,725 |
1,59 |
4 |
0,255 |
1,365 |
5 |
0,5675 |
1,527 |
6 |
0,4865 |
1,4595 |
7 |
0,5203 |
1,5081 |
8 |
0,4959 |
1,4879 |
9 |
0,5061 |
1,5024 |
10 |
0,4988 |
1,4964 |
11 |
0,5018 |
1,5007 |
12 |
0,4996 |
1,4989 |
13 |
0,5005 |
1,5002 |
|
|
|
43
Представим |
матрицу коэффициентов А в виде суммы |
A A1 |
D A2 , |
где |
||
A1 i j ai j, |
i j |
- нижняя треугольная матрица с нулевой диагональю; A2 |
i j ai j, |
i j |
||
- верхняя треугольная матрица с нулевой |
диагональю; D i j ai j, |
i j - |
диагональная |
|||
матрица. Теперь систему уравнений Ax = f |
можно представить в виде: |
|
|
|||
|
|
Ax (A1 D A2 )x f, |
|
|
|
|
|
|
Dx f (A1 A2 )x, |
|
|
|
|
и метод Якоби будет выглядеть следующим образом: |
|
|
|
|||
|
|
Dx(n 1) f (A1 A2)x(n) . |
|
|
|
|
Учитывая, что A1 A2 A D , последнее выражение можно |
также представить в |
|||||
форме |
|
|
|
|
|
|
|
|
D(x(n 1) x(n) ) Ax(n) f . |
|
(2.10) |
||
Y 
3
4x + 2y = 5
2
1
|
|
|
3x + 5y = 9 |
0 |
|
|
X |
0 |
1 |
2 |
3 |
Рис. 2.1. Схема выполнения метода Якоби
44

Метод Зейделя10
Преобразуем выражение (2.9) к виду
(n 1) |
|
1 |
|
i 1 |
m |
|
|
|
|
(n 1) |
(n) |
i 1,m , |
(2.11) |
||||
xi |
|
fi |
ai jxj |
ai jxj |
, |
|||
|
|
ai i |
j 1 |
j i 1 |
|
|
|
|
где n - также номер очередной неизвестной предыдущих величин.
выполняется условие:
итерации. В отличие от метода Якоби, теперь для вычисления используются найденные на этой же итерации значения всех Как и ранее, вычислительный процесс заканчивается, когда
max x(jn 1) x(jn)
x(jn 1) x(jn) , 1 j m
, 1 j m
e>0 - заданная точность вычисления результата.
Пример 2.4. Рассмотрим систему алгебраических уравнений, указанную в предыдущем примере:
4x 2y 5,
3x 5y 9.
Представим полученные выражения в виде итерационной схемы:
|
(n 1) |
|
5 2y |
(n) |
|
x |
|
4 |
|
, |
|
|
|
|
|
|
|
|
|
|
|
(n 1) |
|
|
|
|
9 3x |
||
|
|
|
. |
||
y(n 1) |
|
||||
|
|
|
5 |
|
|
|
|
|
|
|
|
Это означает, что для нахождения величины y на (n+1) итерации используется значение x, только что вычисленное на этой же итерации. В качестве начального
приближения также примем x(0) 0, |
y(0) 0. Результаты расчетов сведены в табл. 2.2. На |
|||
рис. 2.2 графически показан ход выполнения итерационной процедуры Зейделя. |
|
|||
Как и в предыдущем случае, представим матрицу коэффициентов А в виде суммы |
||||
A A1 D A2 |
с теми же обозначениями. Метод Зейделя можно представить в форме |
|||
|
(A1 |
D)x(n 1) |
f A2x(n) . |
|
Учитывая, |
как и ранее, что A2 |
A A1 |
D , последнее выражение можно записать в |
|
виде итерационной схемы |
|
|
|
|
|
(A1 D) (x(n 1) x(n)) Ax(n) f . |
(2.12) |
||
Таблица 2.2
10 Зейдель Филипп Людвиг [24.10.1821 - 13.8.1896] - немецкий астроном и математик. С 1851 стал членом Баварской академии наук; с 1854 - членом Геттингенской академии наук.
45

Результаты выполнения итерационной процедуры метода Зейделя
n |
x(n) |
y(n) |
|
|
|
0 |
|
0 |
1 |
1,25 |
|
|
|
1,05 |
2 |
0,725 |
|
|
|
1,365 |
3 |
0,5675 |
|
|
|
1,4595 |
4 |
0,5203 |
|
|
|
1,4879 |
5 |
0,5061 |
|
|
|
1,4964 |
6 |
0,5018 |
|
|
|
1,4989 |
7 |
0,5005 |
|
|
|
1,4997 |
|
|
|
Y
3
4x + 2y = 5
2
1 
|
|
|
3x + 5y = 9 |
0 |
|
|
X |
0 |
1 |
2 |
3 |
Рис. 2.2. Схема выполнения метода Зейделя
46
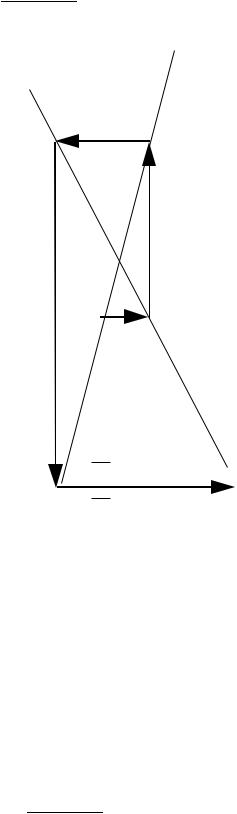
Сходимость итерационных методов
Сравнивая формулы (2.10) метода Якоби и (2.12) метода Зейделя, можно заметить, что
если методы сходятся, то есть в некотором смысле |
x(n 1) x(n) 0, |
n , то они |
||||||||
сходятся к решению исходных задач Ax(n) |
f, |
n . |
|
|
|
|||||
Пример 2.5. Рассмотрим еще одну систему алгебраических уравнений, несколько |
||||||||||
отличающуюся от приведенных в предыдущих примерах: |
|
|||||||||
|
|
4x 2y 5, |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20x 5y 25,. |
|
|
|
||||||
Точное решение этой системы x = 0,5, |
y = 1,5 . |
|
|
|
|
|||||
Для решения воспользуемся методом Зейделя. Как и ранее, представим уравнения в |
||||||||||
виде итерационной схемы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(n) |
|
|
|
|
|
|
|
|
5 2y , |
|
|
|
|||
|
x(n |
1) |
|
|
|
|||||
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
(n 1) |
|
|
|
|
|
25. 20x |
. |
|
|
|||||
|
|
|
|
|||||||
|
y(n 1) |
|
|
|
||||||
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Результаты расчетов сведены в табл. 2.3. На рис. 2.3 отражен ход выполнения |
||||||||||
процедуры Зейделя. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2.3 |
Результаты выполнения итерационной процедуры метода Зейделя |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
x(n) |
|
|
y(n) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0,0 |
|
|
|
1 |
|
|
|
1,25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4,5 |
|
|
|
2 |
|
|
-1,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-4,5 |
|
|
|
3 |
|
|
|
3,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
13,5 |
|
|
|
4 |
|
|
-5,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-22,5 |
|
|
|
5 |
|
|
12,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
49,5 |
|
|
|
6 |
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Результаты расчетов показывают, что в последнем случае отсутствует сходимость последовательности результатов к точному решению. Это приводит к необходимости определения условий сходимости той или иной итерационной процедуры.
47
В общем случае итерационные методы решения систем линейных алгебраических уравнений можно записать в канонической форме
(n 1) |
x(n 1) x(n) |
|
(n) |
|
n 01,,..., |
(2.13) |
B |
(n 1) |
Ax |
|
f, |
где B(n 1), (n 1) - итерационные параметры.
|
|
|
|
|
|
|
|
Y |
|
|
|
-20x + 5y = -2.5 |
|
|
|||||||
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
-5 |
-4 |
-3 |
-2 |
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-1 |
|
|
|
4x + 2y = 5 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
- |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
5 |
|
|
|
|
|
|
|
|
Рис. 2.3. |
Отсутствия сходимости |
|
при использовании метода Зейделя |
||||||||||||||||||
|
|||||||||||||||||||||
В случае, если B(n 1), (n 1) не зависят от номера итерации, метод называется
стационарным. В частности, для метода Якоби B(n 1) D, (n 1) 1; для метода Зейделя
B(n 1) A1 D, (n 1) 1.
Если B(n 1) Е , метод называется явным; в случае B(n 1) Е - неявным.Примеры итерационных методов:
- явный стационарный метод простых итераций
x(n 1) x(n) Ax(n) f ;
48

- неявный стационарный метод верхней релаксации
D wA1 |
x(n 1) x(n) |
Ax(n) f, |
w 0. |
|
w |
|
|
Введем пространство H Rm m - мерных векторов со скалярным произведением
m
u,v uivi
i 1
и нормой
m
 w
w
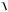 w,w
w,w  w2i .
w2i .
i 1
Определим матричное неравенство: квадратная матрица C > 0 тогда и только тогда,
когда
Cx,x 0 x H,x 0.
Иначе это определение может быть записано следующим образом:
0, |
Cx,x x 2, |
x 0. |
Чтобы определить величину , рассмотрим два случая:
1. Пусть симметричная матрица С > 0, тогда согласно первоначальному определению квадратичная форма11 (Сx,x) > 0 . Но квадратичную форму можно привести к каноническому виду в главных осях:
|
|
m |
m |
|
|
Cx,x ci jxjxi |
i 2i , |
|
|
|
|
i,j 1 |
i 1 |
|
где i |
- собственные числа матрицы С; i - главные координаты. |
|||
|
m |
|
|
|
В силу С > 0 |
имеем i 2i |
0, вследствие чего i 0, |
i 1,m, и отсюда получаем |
|
|
i 1 |
|
|
|
m m
Cx,x i 2i min 2i min 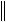
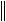 2 , i 1 i 1
2 , i 1 i 1
то есть в качестве может быть взято наименьшее собственное значение матрицы С.
2. Если С - несимметричная матрица, поступают следующим образом для определения
:
m
Cx,x ci jxjxi ,
i,j 1
11 Согласно [7], квадратичная форма определяется только для симметричных матриц.
49

m |
m |
m |
|
x,CTx xi ciTjxj |
cjixjxi, |
ciTj cji . |
|
i 1 |
j 1 |
i,j 1 |
|
В последнем соотношении индексы суммирования можно поменять местами:
m
x,CTx ci jxixj
i,j 1
Теперь очевидно, что Cx,x x,CTx . Поскольку Cx,x 0, то и x,CTx 0. |
|||||||||
Построим матрицу C 1 C CT : |
|
|
|
|
|||||
|
|
|
|
2 |
|
|
|
|
|
|
|
ci j 21 ci j ciTj 12 ci j cji 12 cTji cji ciTj, |
|
|
|||||
но это означает, что построенная матрица является симметричной. Кроме того, |
|||||||||
|
1 |
C C |
T |
x,x |
1 m |
1 |
m |
m |
|
Cx,x |
2 |
|
ci j cji xjxi |
|
ci jxjxi |
cjixjxi |
|
||
|
|
|
|
2i,j 1 |
2 i,j 1 |
i,j 1 |
|
||
1 Cx,x 1 x,CTx Cx,x 0 2 2
в силу предыдущих соотношений.
Это, в свою очередь, означает, что Cx,x 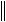 x
x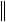 2,
2,
значение матрицы C 12 C CT . Следовательно,
Cx,x Cx,x 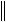 x
x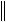 2
2
min - наименьшее собственное
,
то есть указанное выше дополнительное определение положительности имеет место и для несимметричной матрицы.
Оценка
Cx,x  x
x 2
2
позволяет утверждать, что существует обратная матрица C 1 , так как в случае положительной определенности матрицы все ее главные (угловые) миноры положительны
(критерий Cильвестра12, [7]).
12 Сильвестр Джеймс Джозеф [3.9.1814 - 15.3.1897] - английский математик. Окончил Кембриджский университет в 1837 году. С 1855 по 1870 годы являлся профессором Королевской академии в Вулидже; с 1876 по 1883 год - профессором университета Джона Хопкинса в г. Балтиморе; с 1883 года - профессором Оксфордского университета. С 1872 года - иностранным членом-корреспондентом Петербургской академии наук.
50
