Boyarshinov_ChM_T1

где вид матрицы F X(n) определен выше. Сравнение формулы (3.12) с выражением (3.10)

позволяет определить итерационные параметры:

B(n 1) F X(n) , (n 1) 1.

Соотношение (3.12) позволяет построить вычислительный итерационный алгоритм:

X(n 1) X(n) F X(n) 1 F X(n) .

Теорема 3.4. Пусть выполнены условия:

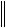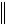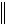1. Оператор F(X) определен в замкнутом шаре X X(0) r, дважды дифференцируем там, при этом вторая производная ограничена F X M .

2. F X(0) имеет обратный оператор, для нормы которого выполнена оценка

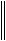F X(0) 1 D.

3. Для начального приближения X(0) верно неравенство

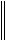F X(0) 1 F X(0) S.

4. Величины M, D, S удовлетворяют условию

H M D S 1. 2

5.Для числа r верно неравенство

1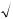1 2H S r . H

89

Тогда:

- в заданном шаре радиуса r уравнение F(X) = 0 имеет решение;

- в вычислительном процессе Ньютона (3.12) приближение X(n) может быть построено при любом значении n ; все X(n) принадлежат шару и последовательность X(n)

где ~t есть наименьший корень уравнения

1Mt2 1 t S 0, 2 D D

t(n) - приближение к нему, построенное при начальном приближении t(0) 0.

Доказательство теоремы 3.4 приведено в книге [4].

В качестве модификации метода Ньютона (3.12) может рассматриваться вариант

итерационный процесс строится так, что из каждого уравнения системы определяется значение только одной неизвестной xin 1 , а значения остальных берутся с предыдущего шага,

При этом определение искомой величины xin 1 на очередной итерации производится с помощью какого-либо известного метода решения одного нелинейного уравнения.

Нелинейный вариант метода Зейделя

В отличие от метода Якоби при определении неизвестной xin 1 на очередной итерации

используются уже найденные предыдущие неизвестные:

fi x1(n 1), x(2n 1), , x(in11), x(in 1),x(in1), , x(mn) 0, i 1,m.

90

Пример 3.4. Решить систему нелинейных алгебраических уравнений

x2 y2 5,

y x2 0.

Решение этой системы нелинейных уравнений с погрешностью 5 10 10 имеет вид:

где i 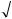1 - комплексная единица.

Воспользуемся методом Ньютона для отыскания корней уравнений этой системы.

f1 x,y x2 y2 5;

f2 x,y y x2;

Представим итерационный процесс Ньютона в форме:

F X(n) X(n 1) F X(n) X(n) F X(n) ;

В явной форме решение полученной системы имеет вид

91

y(n) 2 5

y(n 1) .

2y(n) 1

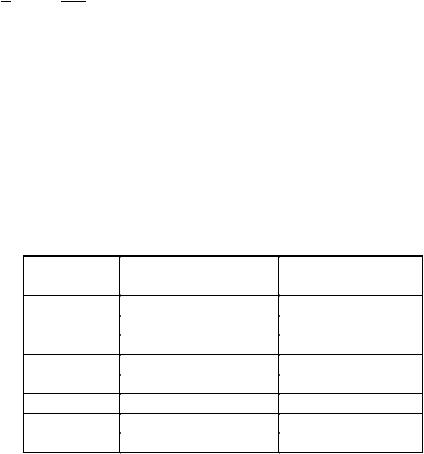
Результаты расчетов приведены в табл. 3.4.

Таблица 3.4

Решение методом Ньютона системы нелинейных уравнений из примера 3.4

Контрольные вопросы и задания

Сформулируйте задачу о нахождении корней нелинейного уравнения.

Опишите метод половинного деления для вычисления корней нелинейного

уравнения. Поясните геометрический смысл метода половинного деления.

Опишите метод простых итераций для вычисления корней нелинейного уравнения.

Поясните геометрический смысл этого метода.

Сформулируйте критерии остановки итерационного вычислительного процесса при

определении корней нелинейного уравнения. Сходимость (расходимость)

итерационного решения.

Сформулируйте условия сходимости метода простых итераций для одного

нелинейного уравнения.

Опишите метод Ньютона для вычисления корней нелинейного уравнения.

92

Поясните геометрический смысл метода Ньютона.

Сформулируйте условия сходимости метода Ньютона для нелинейного уравнения.

Приведите возможные модификации метода Ньютона для определения корней нелинейного уравнения.

Применение метода простых итераций для решения системы нелинейных уравнений.

Сформулируйте условия сходимости метода простых итераций для системы нелинейных уравнений.

Поясните порядок применение метода Ньютона для решения системы нелинейных уравнений.

Сформулируйте условия сходимости метода Ньютона для системы нелинейных уравнений.

Опишите решение системы нелинейных уравнений методом Якоби.

Опишите решение системы нелинейных уравнений методом Зейделя.

93

k 0

где k x - линейно независимые функции; при наличии линейно зависимых составляющих,

от них можно избавиться, уменьшая тем самым число слагаемых в разложении (4.2).

Очевидно, что функция j(x) определяется набором параметров ak, k 0,n , от которых зависит линейно. В противном случае говорят о нелинейной интерполяции.

Учитывая формулу (4.1), получаем

был отличен от нуля, то есть 0.

Интерполяция степенными функциями

Пусть в качестве системы функций k x рассматриваются полиномы

94

В этом случае принимает вид определителя Вандермонда24

единственным образом.

Интерполяционный многочлен Ньютона

Для произвольной функции y(x) определим разделенные разности: - первая разделенная разность

y xi,xj y xi y xj , xi xj

- вторая разделенная разность

y xi,xj,xk y xi,xj y xj,xk , xi xk

- третья разделенная разность

y xi,xj,xk,xl y xi,xj,xk y xj,xk,xl , xi xl

и так далее.

Рассмотрим геометрический смысл разделенных разностей. Очевидно, что y xi,xj и

являются аналогами первых производных функции y(x) на соответствующих

отрезках xi,xj и xj,xk . Вторая разделенная разность y xi,xj,xk аппроксимирует вторую производную функции y(x) на отрезке xi,xk . Соответственно, третья разделенная разность - аналог третьей производной на отрезке xi,xl , и так далее.

Пусть Pn x - искомый интерполяционный многочлен. Запишем для него разделенные

95

P x,x0,x1 P x,x0 P x0,x1 ,

x x1

P x,x0,x1,x2 P x,x0,x1 P x0,x1,x2 , ...

x x2

Отсюда получаем выражение для полинома в виде схемы Горнера25:

Pn x Pn x0 P x,x0 x x0

Pn x0 x x0 P x0,x1 x x1 P x,x0,x1

Pn x0 x x0 P x0,x1 x x1 P x0,x1,x2 x x2 P x,x0,x1,x2 ...

Иначе это выражение можно записать в такой форме:

Pn x Pn x0 x x0 P x0,x1

x x0 x x1 P x0,x1,x2 x x0 x x1 x x2 P x,x0,x1,x2

Pn x y x0 x x0 y x0,x1 x x0 x x1 y x0,x1,x2 ,

либо по схеме Горнера

Pn x y x0 x x0 y x0,x1 x x1 y x0,x1,x2 .

Пример 4.1. Построить аппроксимацию функции sin(x) на отрезке [0, p/2].

Таблица 4.1

25 Горнер Уильям Джордж [1786 - 22.9.1837] - английский математик.

96

Таблица для интерполяции функции sin по 4 точкам

Идея метода обратной интерполяции заключается в построении полинома Ньютона для функции x(y) по заданной зависимости y(x). Особенность данного случая -

необходимость построения полинома Ньютона на сетке с переменным шагом по координате yi .

Таблица 4.2

Таблица для построения обратной интерполяции функции x(y)

97

Интерполяционный полином Ньютона имеет вид x(y) 025. y 1083564434. [0490578385.

y 0573961875.{ 0077430171. y 0046234976. 0013912025. }].

Для y = 0 получаем: x(0) = 0,73301752. Точное решение x = 0,732941247 (невязка уравнения при этом корне равна 5 10 10 ). Относительная погрешность вычисления корня равна 0,0104 % .

Интерполяционная формула Лагранжа

Идея записи интерполяционного полинома Лагранжа заключается в следующем:

k 0

то есть в каждой точке x значение полинома Pn x определяется как линейная комбинация табличных значений.

Воспользуемся условием (4.1) :

то есть на отрезке интерполяции [a, b] каждая из функций Ck x должна иметь n корней.

Вполне естественно представить Ck x в виде полиномов

Ck x k x x0 x x1 x xk 1 x xk 1 x xn ,

k - нормировочный коэффициент, определяемый из условия, что Ck xk 1, то есть

1

k xk x0 xk x1 xk xk 1 xk xk 1 xk xn .

Теперь можно записать полином Лагранжа в общем виде:

Погрешность полинома Ньютона (Лагранжа)

Погрешность представления функции полиномом оценим разностью

98