
Boyarshinov_ChM_T1
.pdf
|
|
i i |
, |
j i |
i 1,m . |
|
|
|
|
ki j |
|
, |
|
|
|||
|
0, |
|
j i |
|
|
|
|
|
Теперь матрицу А можно представить разложением |
|
|
||||||
|
|
A = NKU. |
|
|
|
(2.5) |
||
Благодаря симметрии матрицы |
А имеет место |
равенство |
AT A, что |
позволяет |
||||
произвести следующие преобразования: |
|
|
|
|
|
|
|
|
|
UTKTNT NKU , |
|
|
|
||||
|
UTKT NKU NT 1 |
, |
|
|
||||
|
N 1UTKT KU NT 1 , |
|
|
|||||
|
K 1N 1UTK T U NT 1 . |
|
|
|||||
В силу того, что |
K 1, KT являются |
диагональными матрицами, N 1,UT |
- нижние |
|||||
треугольные, U, NT 1 |
- верхние треугольные, |
в левой части |
последнего |
равенства |
||||
находится нижняя треугольная матрица, а в правой части - верхняя треугольная. Равенство возможно лишь при условии, что и в левой, и в правой частях этого тождества расположены диагональные матрицы.
Матрицы NT 1 |
и |
U |
имеют единицы на главной диагонали; следовательно, их |
||||||
произведение также содержит единичную главную диагональ, то есть |
|||||||||
|
|
|
|
|
U NT 1 E, U NT . |
|
|
||
Отсюда следует, что соотношение (2.5) можно переписать в виде |
|||||||||
|
|
|
|
|
A NKNT . |
|
|
||
Далее, представим матрицу K в виде |
|
|
|
|
|||||
|
|
|
|
|
K K 1/2 D K 1/2 , |
|
|
||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 0 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|||
|
|
1/2 |
|
0 |
2 2 |
0 |
|
0 |
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
, |
||
|
|
|
|
0 |
33 |
|
|||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
|
m m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
31

sign( 11) |
0 |
|
0 |
0 |
|
|
|
0 |
sign( |
2 2) |
0 |
0 |
|
|
|
|||||
D |
0 |
0 |
|
sign( 33) |
0 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
0 |
sign( m m) |
|
|
|
|
||||
Сравнивая теперь |
соотношение |
A N K 1/2 D K 1/2 NT |
с формулой (2.4), |
|||
получаем для матрицы S выражение S |
K 1/2 NT , то есть верхнюю треугольную матрицу с |
|||||
положительными элементами на главной диагонали. Таким образом, конструктивно показано разложение (2.4).
Обозначим y Sx, z DSx, тогда алгоритм метода квадратного корня
ST D Sx f можно рассматривать как последовательность трех процессов:
1)STz f , то есть вычисление решения z системы уравнений с нижней треугольной матрицей;
2)Dy = z , вычисление решения системы уравнений с диагональной матрицей;
3)Sx = y , определения из системы уравнений с верхней треугольной матрицей искомого решения.
Построим разложение вида (2.4) для симметричной матрицы третьего ранга:
|
|
a |
|
a |
|
a |
|
|
|
|
s |
s |
s |
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
13 |
|
|
|
13 |
|
|
d |
|
|
|
|||||||||
|
|
11 |
|
12 |
|
|
|
11 |
12 |
|
|
|
|
|
11 |
d22 |
|
|
|||||
A |
a21 a22 |
a23 |
, |
S |
|
0 |
s22 |
s23 |
, |
D |
|
0 |
0 |
|
; |
||||||||
|
|
|
|
a32 |
a |
|
|
|
|
0 |
|
|
|
|
|
|
0 |
0 |
|
|
|
||
|
a31 |
33 |
|
|
|
0 s33 |
|
|
|
d33 |
|
||||||||||||
|
s11 |
0 |
0 |
|
d11 0 |
0 |
|
s11 s12 |
||||||||||||
ST D S |
s |
s |
22 |
0 |
|
|
|
0 |
d |
22 |
0 |
|
|
|
0 |
s |
22 |
|||
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
s |
s |
23 |
s |
33 |
|
|
|
0 |
0 |
d |
33 |
|
|
|
0 |
0 |
|||
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
s13 s23
s33
|
|
s |
d |
0 |
0 |
|
|
|
s |
s |
|
|
|
11 11 |
s22d22 |
|
|
|
|
11 |
12 |
|
s12d11 |
0 |
|
|
|
0 |
s22 |
|||
|
|
|
|
s23d22 |
s33d |
|
|
|
0 |
0 |
|
s13d11 |
33 |
|
|
||||||
s13 s23
s33
|
|
2 |
s11s12d11 |
|
|
s11s13d11 |
|
|
|
|
|||
|
|
s11d11 |
|
|
|
|
|
|
|||||
s11s12d11 |
s122 d11 s222 d22 |
|
s12s13d11 s22s23d22 |
. |
|
|
|
||||||
|
|
|
s12s13d11 s22s23d22 |
2 |
|
2 |
2 |
|
|
|
|
||
|
s11s13d11 |
s13d11 s |
23d |
22 s33d33 |
|
|
|
|
|||||
Положим d11 sign(a11), тогда из уравнения a |
11 |
s2 d |
11 |
получим |
s |
a |
11 |
. |
|||||
|
|
|
|
|
11 |
|
|
11 |
|
|
|||
Далее, из уравнения a12 s11s12d11 следует, что
32
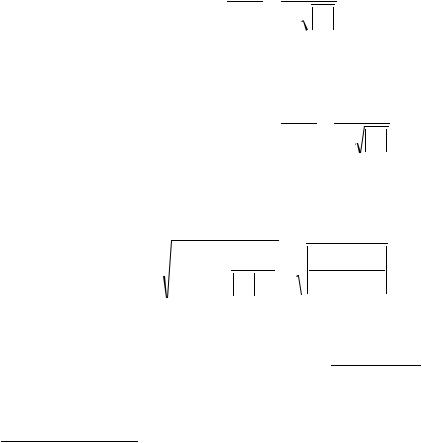
s |
a12 |
a12 |
12 |
d11s11 |
. |
|
d11 a11 |
В силу условия det(A) 0 и теоремы 2.2 можно ожидать, что a11 0. Аналогично можно вычислить
|
a |
13 |
s s d |
11 |
, |
s |
a13 |
|
|
a13 |
|
; |
|||
|
|
11 13 |
|
13 |
|
d11s11 |
|
d11 |
a11 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
a22 s122 d11 s222 d22, |
s222 d22 |
a22 |
s122 d11 . |
|||||||||||
Полагая d22 sign a22 s122 d11 , получим |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
a |
2 |
|
a |
a |
22 |
a |
2 |
|
|
|
s22 |
a22 d11 a |
12 |
|
|
11 |
|
|
12 |
0 |
|||||
|
11 |
d2 |
|
a d2 |
|
||||||||||
|
|
|
|
|
|
11 |
|
|
11 |
|
11 |
|
|
||
- в силу упомянутого условия det(A) 0. |
|
|
|
|
|
|
|
|
|
|
|||||
|
a23 s12s13d11 s22s23d22, |
s23 |
a23 |
|
s12s13d11 ; |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
d22s22 |
||
a33 s132 d11 s232 d22 |
s332 d33, |
|
s332 d33 a33 |
s132 |
d11 s232 d22, |
d33 sign a33 s132 d11 s232 d22 , |
|||||||||
s33 
 a33 s132 d11 s223d22
a33 s132 d11 s223d22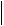 .
.
Нетрудно убедиться, что также s33 0.
Рассмотрим процедуру построения матриц S и D в случае произвольного числа уравнений m.
Верхняя треугольная матрица S si j по определению имеет нулевые элементы:
si j 0, |
i j. |
(2.6) |
Диагональная матрица D может быть определена формально с использованием символа Кронекера D di j i j . Теперь можно подсчитать результат перемножения
матриц:
m |
|
di isi j , |
|
|
DS di ksk j |
|
|
||
k 1 |
|
|
|
|
A STDS |
m |
|
m |
|
siTkdk ksk j |
sk idk ksk j . |
|||
|
k 1 |
|
k 1 |
|
Из последнего выражения с учетом соотношения (2.6) получаем систему алгебраических уравнений:
33

i |
|
|
|
|
|
i 1 |
|
|
|
|
|
|
ai j sk idk ksk |
j si idi isi j |
|
sk idk ksk j , |
i j 1,m . |
|
|
||||||
k 1 |
|
|
|
|
|
k 1 |
|
|
|
|
|
|
При i = j получаем соотношения для вычисления диагональных значений матриц |
S и |
|||||||||||
D: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
a j j |
s2j jd j j s2k jdk k , |
j 1,m , |
|
|
||||||||
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
d j j |
|
|
|
s2k jdk |
|
|
|
|
|
|||
sign a j j |
k , |
|
|
|
|
|
||||||
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
sj j |
|
a j j s2k jdk k , |
j 1,m . |
|
|
|||||||
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
“Наддиагональные” элементы матрицы S определяются по формулам |
|
|
||||||||||
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
ai j sk idk ksk j |
i j 2,m . |
|
|
||||||||
si j |
|
k 1 |
|
|
|
, |
|
|
||||
|
|
si idi i |
|
|
|
|
|
|
|
|
|
|
Определение числа операций алгоритма метода квадратного корня |
|
|
||||||||||
Подсчитаем число операций умножения и деления, |
|
необходимых для реализации |
||||||||||
алгоритма метода квадратного корня. |
|
|
|
|
|
|
|
|
|
|
||
1. Факторизация исходной матрицы, то есть вычисление матриц S и D: |
|
|
||||||||||
|
|
m (m 1) |
|
m (m2 |
1) |
; |
|
|
|
|
||
|
|
2 |
|
6 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
2. Выполнение “обратного” хода: |
|
|
|
|
|
|
|
|
|
|
||
|
|
m (m 1) m ; |
|
|
|
|
|
|||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
3. Вычисление m раз значений квадратных корней. |
|
|
|
|
|
|||||||
Общее количество операций равно |
m (m2 9m 2) |
, |
или приблизительно |
m3 |
что |
|||||||
|
|
|
6 |
|
|
, |
||||||
|
|
|
|
|
|
|
|
|
|
6 |
|
|
практически в два раза меньше, чем число операций в алгоритме метода Гаусса.
Пример 2.1. Рассмотрим решение системы двух линейных алгебраических уравнений методом квадратного корня:
0780,x 0717,y 0063,;
0717,x 0659,y 0058,;
34

|
|
|
a12 |
|
|
s11 |
a11 0883176087,; |
d11 1; |
s12 s d |
11 |
0811842633,; |
|
|
|
11 |
|
|
s22 |
a22 s122 d11 000940537,; |
d2 2 1; |
|
|
|
1.STz f,
2.Dy z,
0883176087, |
0 |
|
|
|
|
z1 |
|
0063, |
z1 |
|
0071333453, |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
z |
|
|
|
|
|
||
0811842633, |
000940537, |
|
|
0058, |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
1 |
0 |
y |
|
z |
|
y |
1 |
|
|
|
z |
|
|
0071333453, |
|
|
||||||
|
|
|
1 |
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|||||
0 |
1 |
y |
|
z |
|
y |
|
|
|
z |
|
000940958, |
|
|
||||||||
|
|
|
2 |
|
2 |
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||
|
0883176087, |
0811842633, |
x |
|
y |
|
|
|
3. Sx y, |
|
1 |
|
1 |
|
|||
|
000940537, |
|
|
|
|
|
, |
|
|
0 |
|
x |
|
y |
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
x |
|
10, |
|
Точное решение задачи : |
|
1 |
|
|
|
|
|
. |
|
|
x |
|
10, |
|
|
|
2 |
|
|
x1 |
|
|
100002451, |
|
|
|
|
|
|
|
. |
x |
|
|
|
|
1000007921, |
||
2 |
|
|
Устойчивость системы линейных алгебраических уравнений
Для оценки влияния изменения (возмущения) правой части f и матрицы коэффициентов А на решение x системы линейных алгебраических уравнений Ax = f
введем линейное пространство H векторов размерности m, в котором определим норму,
удовлетворяющую условиям [8]:
x 0 |
x H, x 0; |
x 0 |
x 0; |
 x
x

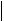
 x
x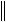 ;
;
 x y
x y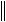
 x
x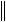
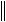 y
y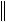 .
.
В пространстве Н в качестве нормы вектора могут быть взяты определения
“кубической” и “сферической” норм [9]:
|
m |
|
x |
x2i , |
x maxxi . |
|
i 1 |
1 i m |
Определим норму матрицы (оператора):
Ax
A sup
x H, x 0 x
 sup Ax .
sup Ax .

 x
x
 1
1
Из последнего определения, в частности, следуют известные соотношения:
35

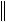 Ax
Ax
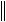 A
A
 x
x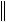 ,
,
 A B
A B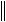
 A
A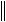
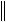 B
B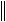 ,
,
 AB
AB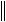
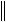 A
A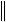
 B
B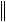 ,
,
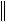 E
E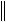 1.
1.
Здесь Е - тождественный оператор, ei j i j, |
i, j 1,m . |
В качестве нормы матрицы А может быть взято определение [8]:
m m
 A
A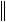
 a2i j ,
a2i j ,
i 1 j 1
либо определение [9]:
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
A max |
|
a |
i j . |
|
|
|
|
|
|
|
1 i m |
|
|
|
|
||
|
|
|
|
|
j 1 |
|
|
|
|
|
|
Пусть ~f - “возмущенная” правая часть системы уравнений. Оценим изменение |
|||||||||
решения x ~x x как следствие изменения правой части |
f |
~f f . |
||||||||
f,~f |
Система |
уравнений Ax=f называется |
устойчивой |
по правой части, если |
||||||
x |
f |
M, |
M 0 - положительная константа. |
|
|
|
||||
|
Это, |
в частности, означает, что x 0 |
при f |
0, то есть имеется непрерывная |
||||||
зависимость решения от правой части. |
|
|
|
|
|
|
||||
Пусть определитель матрицы А отличен от нуля. В этом случае существует обратная
матрица A 1 . В силу линейности системы алгебраических уравнений имеем:
~ ~ ~
A x A(x x) Ax Ax f f f,
x A 1 f,
 x
x
 A 1 f
A 1 f
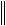 A 1
A 1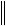
 f
f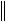 ,
,
отсюда следует
x A 1 |
f |
(2.7) |
и роль константы М может выполнять 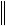 A 1
A 1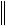 . Чем ближе значение det(A) к нулю, тем больше величина
. Чем ближе значение det(A) к нулю, тем больше величина 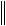 A 1
A 1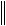 , тем значительнее отклонение x при возмущении f .
, тем значительнее отклонение x при возмущении f .
Из уравнения Ax = f следует оценка
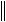 f
f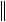
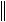 Ax
Ax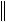
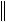 A
A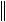
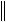 x
x .
.
Перемножая два последних неравенства, получаем
36

|
|
x f A 1 f A x , |
||
|
|
x |
f |
f |
|
|
A 1 A |
MA |
, |
|
|
x |
f |
f |
где MA |
A 1 |
A - число обусловленности матрицы А, характеризующее зависимость |
||
относительной погрешности решения системы уравнений от относительного “возмущения” правой части. Очевидно, что
1  E
E
 A A 1
A A 1
 A
A
 A 1
A 1 MA .
MA .
Пример 2.2. Рассмотрим систему уравнений
0780,x 0563,y 0217,,
0913,x 0659,y 0254,.
Определитель этой системы уравнений |
D 0780, 0659, 0563, 0913, 0000001, 10 6 |
||
отличен от 0, хотя и мал. Матрица коэффициентов представляется в виде |
|||
|
0780, |
|
0563, |
|
A |
|
. |
|
|
|
|
|
0913, |
|
0659, |
Вычисление обратной матрицы приводит к значению |
|||
A 1 |
659000 |
|
563000 |
|
|
. |
|
|
|
|
|
|
913000 |
780000 |
|
Нетрудно убедиться, что определитель обратной матрицы принимает значение
D 659000 780000 563000 913000 1000000 106 .
При использовании для вычисления нормы матрицы выражения
|
m m |
|
A |
a2i j |
|
|
i 1 j 1 |
|
получаем для рассматриваемого случая: |
|
|
A 1480952059,, |
A 1 |
1480952059,. |
Теперь можно оценить число обусловленности матрицы А, то есть показатель устойчивости решения при возмущении правой части системы уравнений:
MA 2193219.
Рассмотрим случай одновременного возмущения и правой части f, и матрицы коэффициентов A:
37

~~ |
~ |
~ |
|
|
Ax f, |
A A A . |
|
||
Для получения полной оценки погрешности решения системы алгебраических |
||||
уравнений необходимо рассмотреть вспомогательное утверждение: |
|
|||
Лемма 2.1. Пусть С - квадратная матрица, |
C 1; Е - единичная матрица. Тогда |
|||
существует E C 1, причем |
|
|
|
|
E C 1 |
1 |
|
||
|
|
1 C . |
|
|
Доказательство |
|
|
|
|
Для любого x имеет место неравенство |
|
|
|
|
E C x x Cx x Cx x C x 1 C x x , |
(2.8) |
|||
где 1  C
C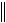 0 - по условию леммы.
0 - по условию леммы.
Рассмотрим однородное уравнение (E + C)x = 0. Из неравенства (2.8) следует
 E C x
E C x
 0
0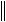
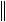 x
x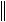 ,
,
что возможно лишь при 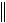 x
x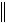 0, откуда следует, что x = 0 . Иными словами, однородное уравнение (E + C)x = 0 имеет только тривиальное решение. Но это означает, что определитель det(E + C) не равен нулю, то есть существует обратная матрица E C 1.
0, откуда следует, что x = 0 . Иными словами, однородное уравнение (E + C)x = 0 имеет только тривиальное решение. Но это означает, что определитель det(E + C) не равен нулю, то есть существует обратная матрица E C 1.
Теперь рассмотрим уравнение
(E + C)x = y,
имеющее решением x E C 1y. С помощью выражения (2.8) получаем
|
|
|
|
|
|
|
E C x x E C 1y , |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
E C |
1 |
y |
E C x |
y |
|
|
|
|
y |
. |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 C |
|
||||||||||
Последним неравенством воспользуемся для подсчета нормы |
|
|||||||||||||||||||||||||||||
E C 1 |
sup |
E C 1y |
sup |
y |
sup |
1 |
1 . |
|||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
|
|
y |
|
|
|
0 |
y |
|
|
|
|
|
y |
|
|
|
0 1 C y |
|
|
|
|
y |
|
|
|
0 |
1 C |
1 C |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Что и требовалось доказать.
Теорема 2.3. Пусть матрица А имеет обратную и выполнено условие
A 1 . A 1
38

~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда матрица A A A имеет обратную и справедлива оценка погрешности |
|||||||||||||||
x |
MA |
|
|
A |
f |
|
|
|
|
||||||
|
|
. |
|
|
|
||||||||||
x |
|
1 MA |
|
A |
|
A |
|
f |
|
|
|
|
|||
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
||
Доказательство |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
~ |
|
1 |
|
|
|
|
|
|
1 |
||||||
|
|
A A E C , C A |
|
||||||||||||
A A A A E A |
|
|
A |
|
|||||||||||
Оценим норму матрицы С с использованием условия теоремы: |
|
||||||||||||||
С A |
1 |
|
|
1 |
A A |
1 |
|
1 |
1. |
|
|||||
A A |
|
|
|
A |
1 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В силу того, что матрица С удовлетворяет условию леммы 2.1, существует матрицаE C 1. Поскольку
|
|
|
|
|
~ 1 |
A E C |
1 |
E C |
1 |
A |
1 |
, |
|
|
|
|
|
|||||||
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
||||||||||
то A~ 1 |
существует в силу существования матриц A 1 и |
E C 1. |
|
|
|
|
|
|||||||||||||||||
Теперь определим отклонение возмущенного решения от исходного: |
|
|
|
|
||||||||||||||||||||
|
~ |
~ 1~ |
1 |
|
~ 1~ |
~ 1 |
~ 1 |
f A |
1 |
~ |
1 |
|
~ |
|
~ |
1 |
A |
1 |
f . |
|||||
|
x x x A f A |
|
f A f A |
f A |
|
|
f A |
|
|
f f |
A |
|
|
|||||||||||
Учитывая, что ~f f f, |
f Ax, получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x A~ 1 f A~ 1 A 1 Ax A~ 1 f A~ 1A A 1A x A~ 1 f A~ 1A E x, |
|||||||||||||||||||||||
откуда можно оценить норму |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
~ 1 |
|
~ 1 |
|
|
~ |
1 |
|
|
~ 1 |
A E x . |
|
|
|
|
||||||||
|
|
x A f A |
A E x A |
|
f A |
|
|
|
|
|||||||||||||||
Оценим порознь слагаемые в правой части этого неравенства:
~ |
1 |
E C |
1 |
A |
1 |
E C |
1 |
A |
1 |
|
A 1 |
A 1 |
|
A |
|
|
|
|
|
|
1 A 1 |
; |
|||||
|
|
|
|
|
|
|
|
|
|
|
1 C |
A |
|
~ 1 1 1
A 1A E A A A E A E A 1 A A E A E C A E
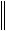 E C 1A 1A E
E C 1A 1A E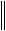
 E C 1 E
E C 1 E
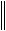 E C 1 E E C
E C 1 E E C 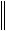
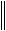 E C 1C
E C 1C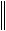
E C 1 C |
C |
|
A 1 A |
A 1 A |
|
|
1 A 1 |
. |
|||
|
1 C |
|
1 A 1 A |
A |
|
Подставим полученные оценки в исходную формулу:
39

A 1 |
|
|
A 1 A |
|
x |
|
A 1 |
|
|
|
|||||
x |
|
f |
|
|
|
|
|
|
f A x . |
||||||
1 A 1 A |
1 A 1 A |
|
|
|
1 A 1 A |
|
|
|
|||||||
Учитывая, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
Ax |
|
f |
A x , |
|
|
|
||||
|
|
f f |
f |
f |
f |
|
|
|
|||||||
|
|
|
f |
|
|
|
|
|
|
|
|
|
|||
имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A 1 |
f |
|
|
|
|
|
A 1 A |
f |
|
A |
|||||
x |
|
|
A x A x |
|
|
|
|
|
x |
||||||
1 A 1 A f |
|
|
|
|
1 A |
1 |
A |
A |
f |
|
A . |
||||
|
|
|
|
|
|
|
|
|
A |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вспоминая, что MA |
A 1 |
A , получаем доказываемое утверждение теоремы |
|||||||||||||
|
|
x |
MA |
|
|
A |
f |
|
|
|
|
||||
|
|
|
|
. |
|
|
|
||||||||
|
|
x |
|
A |
|
|
A |
|
f |
|
|
|
|
||
|
|
|
1 MA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
||
40
