Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пермский национальный исследовательский политехнический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Boyarshinov_ChM_T1

.pdf

Скачиваний:

130

Добавлен:

13.03.2016

Размер:

1.32 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 1816 17 18 > Следующая >>>

	x xk 1/2	2 xk	xk		x xk 1/2	2
f xk 1/2 h f xk 1/2	x xk 1/2			f	x xk 1/2	dx f xk 1/2	h
f xk 1/2 h f xk 1/2	2			f	2	dx f xk 1/2	h
	2	xk 1	xk 1		2
			xk 1

12 xk f x xk 1/2 2 dx .

xk 1

Полученное выражение позволяет оценить погрешность:

xk f

x x

k 1/2

2dx

max

x x

k 1/2

2dx

x x

k 1

xk 1

M2,k x xk 1/2 3

(7.6)

M2,k

O h

xk 1

Здесь обозначено: M2,k

max

f x .

k 1

x x

Формула (7.6) устанавливает, что при ограниченности второй производной на рассматриваемом отрезке погрешность формулы прямоугольников имеет третий порядок.

Для всего отрезка интегрирования [a, b] получаем

b a ,

M2,k M2

(7.7)

k 1

24 k 1

где

maxf x .

x a,b

Иными словами, для всего интервала [a, b] погрешность рассмотренного способа интегрирования имеет второй порядок.

Аналогичным способом можно проверить также часто применяемую на практике формулу интегрирования

f x dx f xk 1 h ,

xk 1

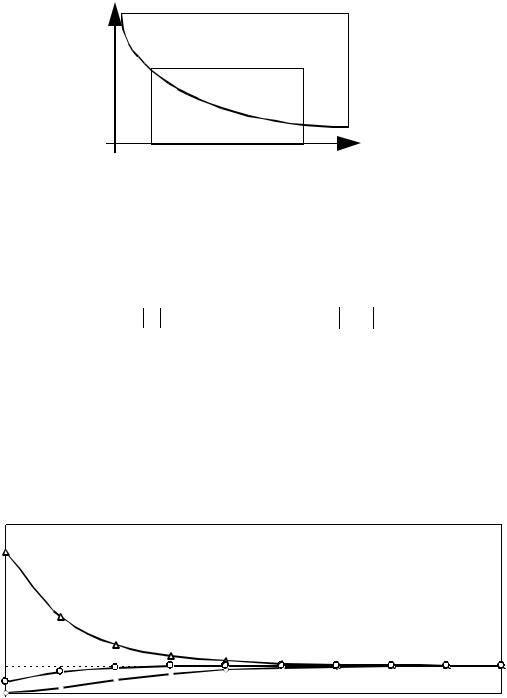
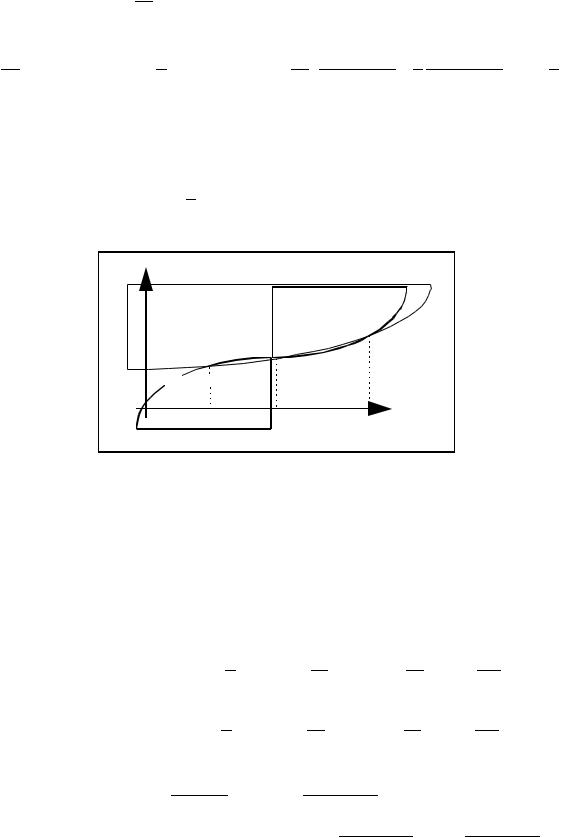
геометрический смысл которой пояснен на рисунке 7.2.

Оценка погрешности интегрирования на отрезке xk 1, xk , выполненная аналогично предыдущему случаю, приводит к результату

2	12	xk
k f xk 1 h2	12	f x xk 1 2dx,
		xk 1

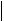k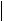 O h2 .

151

xk-1	xk	x

Рис. 7.2. Схема численного интегрирования методом прямоугольников

Для всего интервала [a, b] погрешность интегрирования составляет

M	1h	b a ,	M		maxf x	.
				1
2					x a,b

На рис. 7.3 приведены графики, отражающие сходимость процесса приближенного

вычисления определенного интеграла e xdx с помощью формул метода прямоугольников

с центральной точкой (формула (7.5)), “левой” точкой (рис. 7.2)								и “правой” точкой
				xk
				f x dx f xk h.
				xk 1
6
6
5
5
4
4
3
3
2
2
1
1
0
0
2	4	8	16	32	64	128	256	512	1024 n

Рис. 7.3. Значения интеграла e xdx, вычисленные точно (-------) и по формулам метода

прямоугольников с центральной (- o -), “левой” (- -) и “правой” (- -) точками на сетках

152

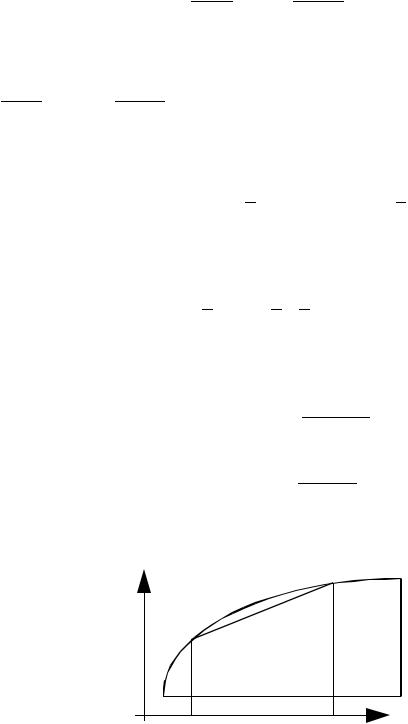
Формула трапеций

Заменим функцию f(x) на отрезке xk 1,					xk	линейным приближением
			f(x) xk x f xk 1 x xk 1				f xk .
				h		h
Это	означает,		что в	разложении		(7.2)	удерживаются две функции
0(x) xk	x,	1(x) x xk 1 .
	h		h
Тогда весовые коэффициенты
			xk	x dx h ,		xk	x dx h.
			C0k 0	x dx h ,	C1k 1		x dx h.
			xk 1	2		xk 1	2
			xk 1			xk 1

Отсюда вытекает формула метода трапеций (рис. 7.4):

f x dx f x

h f x

h h

f x

(7.8)

k 1

xk 1

Воспользуемся формулами Тейлора

f xk 1 f x f x xk 1 x f

xk 1 x

, xk 1,xk ,

f xk f x f x xk x

x 2

xk 1,xk .

xk-1	xk	x

Рис. 7.4. Схема численного интегрирования методом трапеций

153

Оценим погрешность представления (7.8) на отрезке xk 1,							xk :
k	xk	xk		x		x		x x
k	f x 0 x f xk 1 1 x f xk 1 dx		f x		k	f xk 1		h	k 1	f xk dx
	xk 1	xk 1				h		h

xk f x xkh x f x f x xk 1 x f xk 12 x 2

xk 1

	x f xk x	2
x xk 1 f x f x xk	x f xk x		dx
h	2

x x

xk x xk 1 x

xk x x x

f x 1 k

k 1 dx

f x

k 1 dx

xk 1

x 2 x

x 2 x x

k 1

dx.

xk 1

В силу того, что

1 xk x x xk 1 0,

xk x xk 1 x xk x x xk 1 0,

вычисляемая погрешность

x 2

x 2 x x

k 1

dx .

xk 1

Получим оценку погрешности:

max

x x

2h x xk 1,xk

k 1

xk 1

2,k

xk 1 x

x dx

xk x

x xk 1

k 1

2,k

x x

k 1

M2,k

xk 1 x

xk 1

dx h

xk x

k 1

154

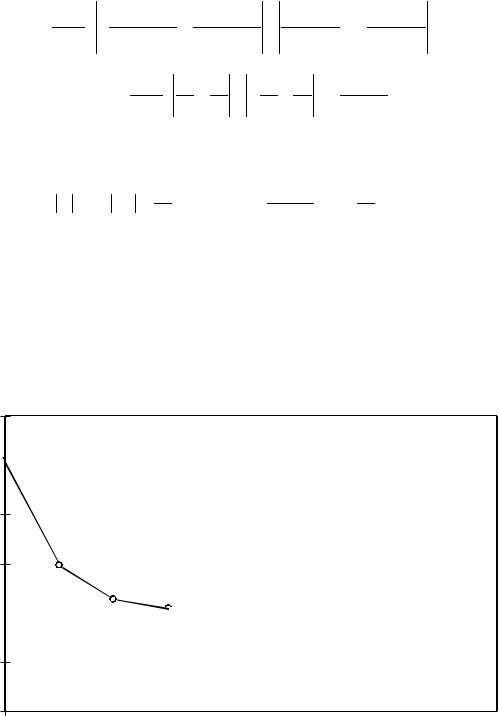
M2,k		x xk 1		3		x xk 1		4			x xk				4		x xk		3	xk
M2,k		x xk 1				x xk 1					x xk				h		x xk
	h	3				4							4		h			3
2h		3				4							4					3
																				xk 1
		M2,k	h4			h4		h4			h4			M		2,kh3
					3				4			3				12		.
		2h			3	4			4			3				12
Погрешность для всего отрезка интегрирования [a, b]
	n		3		n					nh h			2				2
k h					M2,k		M2			nh h				M2		h		b a			(7.9)
k h					M2,k		M2							M2		h		b a			(7.9)
	k 1	12			k 1						12					12

имеет второй порядок.

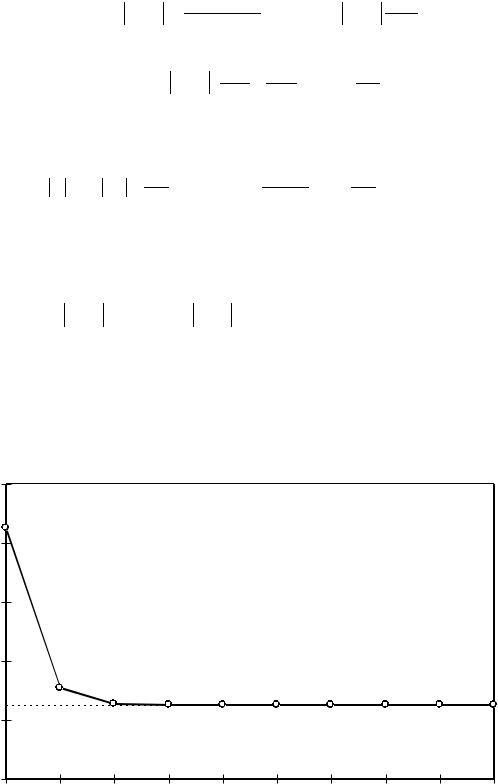
На рис. 7.5 показан график сходимости приближенного значения определенного

интеграла e xdx, полученного с помощью формул метода трапеций.

2.5

1.5

0.5

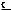
2 4 8 16 32 64 128 256 512 1024 n

Рис. 7.5. Значения интеграла e xdx, вычисленные точно ( ------ ) и по формуле метода

трапеций ( - o - ) на сетках n

155

Формула Симпсона33

Заменим на отрезке xk 1, xk				функцию f(x) полиномом Лагранжа. В частности, для
трех точек xk 1, xk 1 2, xk полином второй степени имеет вид
L2 x	x xk 1 2 x xk f xk 1			x xk 1 x xk f xk 12						x xk 1 x xk 1 2 f xk
	xk 1 xk 1 2 xk 1 xk			xk 1 2 xk 1 xk 1 2 xk						xk xk 1 xk xk 1 2
22 x xk 1 2 x xk f xk 1 2 x xk 1 x xk f xk 1 2 x xk 1 x xk 1 2 f xk .
h
	Это означает, что в разложении (7.2) оставлены три функции:
		0	x 2		x x	k 1/2	x x	k	,
		0		h2		k 1/2		k

1 x 42 x xk 1 x xk , h

x 2

x x

k 1

x x

k 1/2

Для определения коэффициентов C0k, C1k, C2k вычислим интегралы:

C0k

0 x dx 22

x xk 1/2

x xk

22 x xk

xk xk 1/2 x xk dx

xk 1

x xk

h x xk 2 xk

;

x xk

x xk dx

xk 1

k 1

dx 42

C1k 1 x dx 42

x xk 1

x xk

x xk xk xk 1 x xk dx

xk 1

4 xk

x xk 3

x xk

2 xk

2 x xk

dx h x xk dx

;

xk 1

k 1

C2k

2 x dx

x xk 1 x xk 1/2 dx

xk 1

33 Симпсон Томас [20.8.1710 - 14.5.1761] - английский математик. С 1713 года был профессором Вулиджской военной академии, с 1746 года был избран членом Лондонского королевского общества.

Рассматриваемый метод интегрирования иногда называют также методом парабол.

149

2		xk
h	2
		x	k 1

x xk 1/2 xk 1/2 xk 1 x xk 1/2 dx

xk 1

x xk 1/2

x x

2dx h

x x

k 1/2

xk 1

k 1

Формула приближенного интегрирования Симпсона (рис. 7.4):

xk	f xk 1 4f xk 1/2 f xk .
f x dx h	f xk 1 4f xk 1/2 f xk .
6
xk 1

f(x)

xk-1

xk-1/2

xk x

h . 6

(7.10)

Рис. 7.6. Схема численного интегрирования методом Симпсона

Для оценки погрешности выражения (7.10) приближенного интегрирования, как и

ранее, воспользуемся формулами Тейлора для представления

x ,

k вблизи

k 1

точки xk 1/2 :

f xk 1 f xk 1/2 f xk 1/2 h f xk 1/2

f xk 1/2

fiv

384

f xk f xk 1/2 f xk 1/2

f xk 1/2

f xk 1/2 8

384

f x f xk 1/2 f xk 1/2

x x

k 1/2

f xk 1/2

x x

1/2

x x

f xk 1/2

x x

k 1/2

fiv

k 1/2

Здесь принято, что , , xk 1,xk .

150

Подсчитаем интеграл в левой части формулы (7.10):

f x dx

xk 1

x f

x xk 1/2

k 1/2

x xk 1/2

k 1/2

fiv x xk 1/2

xk 1

h f

x xk 1/2

k 1/2

xk 1

Подсчитаем выражение в правой части (7.10):

6 f xk 1 4f xk 1/2 f xk

h		x		f x		h	2
h	2f	x		f x		h
6			k 1/2		k 1/2	4
6						4

h4	fiv fiv	4f x		.
384			k 1/2
384

Определим величину погрешности формулы Симпсона:

f xk 1 4f xk 1/2 f xk

f x dx h

xk 1

x xk 1/2 4

h f xk 1/2 24

f xk 1/2

xk 1

xk 1/2 f xk 1/2

fiv

384

x xk 1/2

xk 1

2304

Модуль погрешности на отрезке xk 1,

xk :

x xk 1/2 4

xk 1

2304

151

max

fiv

xk x xk 1/2 4

max

fiv x h5

k 1

1152

x x

xk 1

max

1152

M4,k

k 1

1920

720

x x

Для всего отрезка [a, b] интегрирования погрешность

b a

M4,k

(7.11)

k 1

720 k 1

720

имеет четвертый порядок.

В последних выражениях использованы обозначения

M4,k	max				fiv x ,	M4	max fiv x .
	x x	k 1	,x	k			x a,b
		k 1		k

На рис. 7.7 изображен график сходимости приближенного значения определенного

интеграла e xdx, полученного с помощью формул метода Симпсона.

1.15

1.11

1.07

1.03

0.99

0.95

2 4 8 16 32 64 128 256 512 1024 n

Рис. 7.7. Значения интеграла e xdx, вычисленные точно ( -------- ) и по формуле метода

Симпсона ( - o - ) на сетках n

152

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 1816 17 18 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
19.07.201978.85 Кб2bilety_43-49.doc
#
13.03.2016105.07 Кб48bilety_fkhma (1).docx
#
22.09.2019260.61 Кб1bilety_po_istorii1_1.doc
#
29.03.2015539.41 Кб6bilety_sgmu.docx
#
29.03.2015545.25 Кб5bilety_sgmu.docx
#
13.03.20161.32 Mб130Boyarshinov_ChM_T1.pdf
#
13.03.20162.93 Mб308Boyarshinov_ChM_T2.pdf
#
13.03.20161.69 Mб99Boyarshinov_ChM_T3.pdf
#
21.08.201955.81 Кб6British Etiquette and Manners.doc
#
01.05.2019559.62 Кб4budget.doc
#
29.03.20153.3 Mб25buhgal.pdf