РАМАЗАНОВА К.Р

201

В соотношении (7.20) замечательное по простоте аппроксимационное выражение для К(ρ) – коэффициент рассеяния для больших оптически «мягких» частиц (α, m ~ 1,00) полученное Ван де Хюлстом [1а, 192].

где ρ = 2α(m – 1) – комбинированный параметр, имеющий физический смысл фазового сдвига электромагнитной волны при её прохождении сферической частицы по диаметру.

Аппроксимационные формулы для характеристических функций – удельной мутности g(α,m) [192-195] и структурного фактора υ(α,m) (7.16) в соответствующих диапазонах -2 ≤ n ≤ 4 следуют из соотношений (7.18)-(7.20).

При получении аппроксимационных выражений волновой экспоненты n(α,m) приведённые выше формулы (7.18)-(7.21) применить нельзя для К(α,m) из-за погрешности вычисления производной в соотношении (7.11). Поэтому наиболее целесообразным является использование аппроксимационных выражений, основанных на результатах точных расчётов n(α,m) по строгой теории Ми [194]. При этом область параметров α и m разбили на интервалы для:

* 1,01≤ m ≤ 1,14:

* 1,14 < m ≤ 1,33:

В диапазонах (7.22) и (7.25) для n(α,m) записали в виде аппроксимационной формулы Хеллера [195], где для параметров k и S нашли зависимости от m:

где k = 1,38 – 0,66•m, S = 2,6•m − 0,75.

Для диапазона (7.23) получили аппроксимационную формулу для n(α,m)

где A0 = 4,57 − 2,6•m, B0 = (7•m – 6) – exp (66,7•m − 78).

Для диапазона (7.24) и (7.26) использовали аппроксимационную формулу для n(α,m) [192] с модифицированным нами поправочным фактором Р1.

где Р1 = 1 – ехр [-12,6•(m – 1)], n(ρ) = 2•[2•(1 – cos ρ)/К(ρ) – 1] [49]. В соотношении

(7.29) n(ρ) – волновой экспонент, полученный по формуле (7.11) из (7.21) в приближении Ван де Хюлста [192].

Результаты расчёта характеристических функций светорассеяния для значений m

= 1,01; 1,05; 1,10; 1,15; 1,20; 1,25; 1,30; 1,33 по формулам (7.18)-(7.29) (формулу для

202

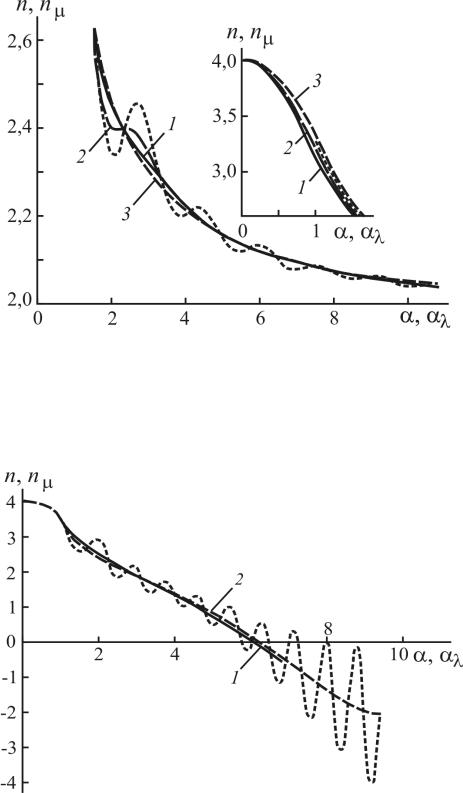
удельной мутности g(α,m) через К(α,m) см. в работе [192]) и формуле (7.16) для υ(α,m), приведённые совместно со значениями для монодисперсных частиц по формуле (7.17) по строгой теории Ми [194], рассчитанные в работе [192], показывают, что полученные аппроксимационные формулы [249а, 250а] аналитически сглаживают осцилляции соответствующих характеристических функций светорассеяния монодисперсных систем (рис. 7.2-7.12).

Рис. 7.2. Зависимость волнового экспонента n и nμ от α и αλ при m = 1,01 для монодисперсных частиц по теории Ми [194] (штрихи), по аппроксимационным формулам: 1 – для полидисперсных систем с 2 – μ = 10, и 3 – μ = 35, где nμ и αλ – полидисперсные аналоги n и α, μ – параметр полидисперсности гамма-распределения

Рис. 7.3. Зависимость волнового экспонента n и nμ от α и αλ при m = 1,33 для монодисперс-

203

ных частиц по теории Ми [194] (штрихи), по аппроксимационным формулам: 1 – для полидисперсных систем с 2 – μ = 10, где nμ и αλ – полидисперсные аналоги n и α, μ – параметр полидисперсности гамма-распределения

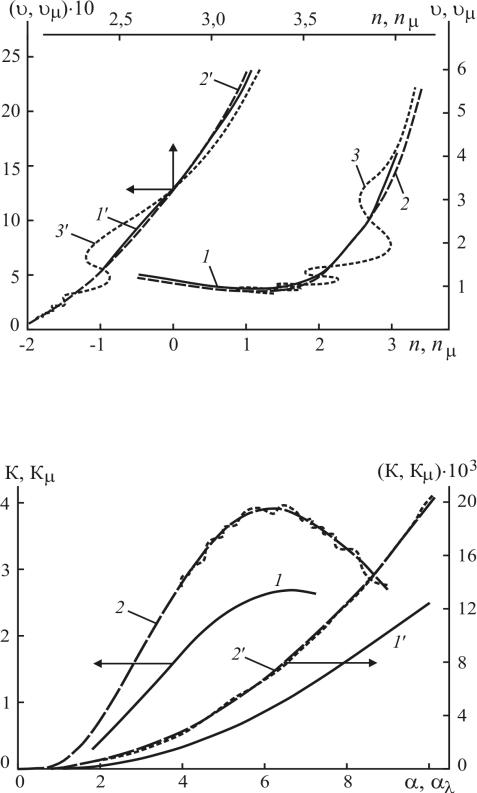
Рис. 7.4. Зависимость структурного фактора υ и υμ от n и nμ при m: (1'-3') –

1,01, (1-3) – 1,33 для монодисперсных частиц: штрихи 3, 3' – по теории Ми [194], 2, 2' – по аппроксимационным формулам, для полидисперсных систем с 1, 1' – μ = 10, где υμ и nμ – полидисперсные аналоги υ и n, μ – параметр полидисперсности гамма-распределения

Рис. 7.5. Зависимость коэффициента рассеяния К и Кμ от α и αλ при m: 1',2' – 1,01, 1,2 – 1,33 для монодисперсных частиц по теории Ми [194] (штрихи), по аппроксимационным формулам: 2, 2' – для полидисперсных систем с 1,1' – μ = 10, где Кμ – полидисперсный аналог К, μ – параметр полидисперсности гамма-распределения

204

Рис. 7.6. Зависимость n от α при m: 1 – 1,054; 2 – 1,10; 3 – 1,15 по аппроксимационным формулам (сплошная линия), по формулам теории Ми [194] (штриховая линия) и по экспериментальным данным [192] (разные длин волн) для водных суспензий мастиксы со среднечисленным радиусом частиц rn = 1,3 мкм и параметром μ = 250 [192] (тёмные кружки)

Рис. 7.7. Зависимость n от α при m: 1 – 1,20; 2 – 1,25 по аппроксимационным формулам (сплошная линия) и по формулам теории Ми [194] (штриховая линия)

205

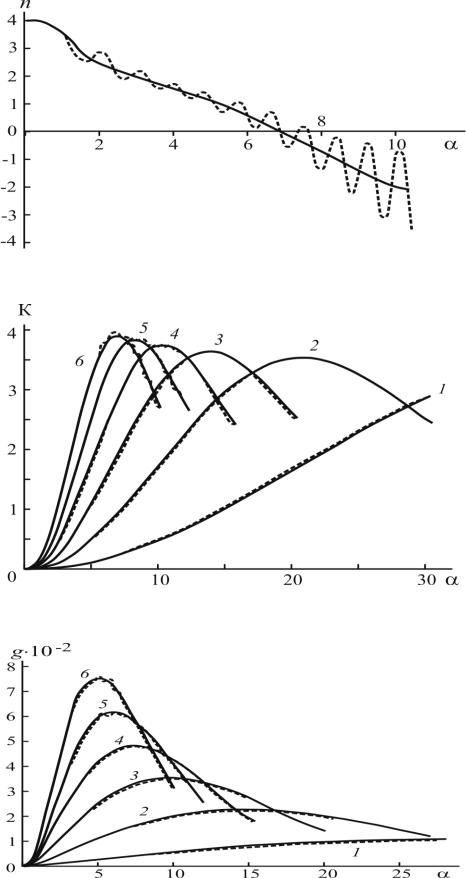
Рис. 7.8. Зависимость n от α при m = 1,30 по аппроксимационным формулам (сплошная линия) и по формулам теории Ми [194] (штриховая линия)

Рис. 7.9. Зависимость К от α при m: 1 – = 1,05; 2 –1,10; 3 – 1,15; 4 – 1,20; 5 – 1,25; 6 – 1,30

по аппроксимационным формулам (сплошная линия) и по формулам теории Ми [194] (штриховая линия)

Рис. 7.10. Зависимость удельной мутности g от α [192] при m: 1 – 1,05; 2 – 1,10; 3 – 1,15; 4

– 1,20; 5 – 1,25; 6 – 1,33 по аппроксимационным формулам коэффициента рассеяния (сплошная линия) и по формулам теории Ми [194] (штриховая линия)

206

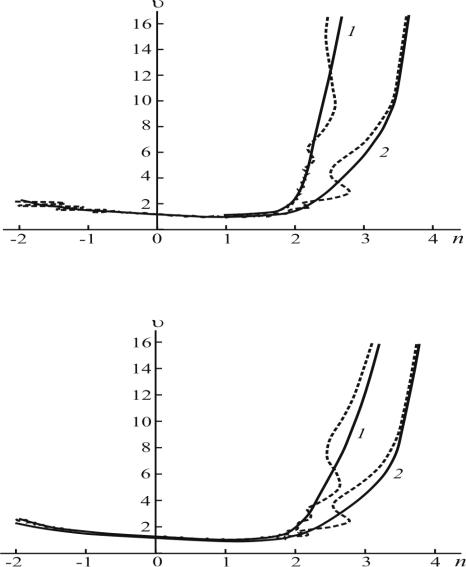
Рис. 7.11. Зависимость υ от n при m: 1 – 1,05, 2 – 1,20 по аппроксимационным формулам коэффициента рассеяния (сплошная линия) и по формулам теории Ми [194] (штриховая линия)

Рис. 7.12. Зависимость υ от n при m: 1 – 1,15 (1), 1 – 1,30 по аппроксимационным формулам коэффициента рассеяния (сплошная линия) и по формулам теории Ми [194] (штриховая линия)

Для физического обоснования аналитического сглаживания при значении относительного показателя преломления, близкого к m ~ 1,00 (нижняя граница диапазона 1,01 ≤ m ≤ 1,33), использовали полученные в работе [192] выражения для полидисперсных аналогов коэффициента рассеяния Kμ(αλ) и волновой экспонент nμ(αλ), рассчитанные по теории Релея-Ганса [1а, 192], где μ – параметр полидисперсности гамма-распределения ансамбля дисперсных частиц.

Для другой границы m = 1,33 исследуемого интервала использовали табличные данные [1а, 192] для среднего фактора эффективности ослабления F = Kμ (в широком интервале μ и αm), рассчитанные для полидисперсных систем с гаммараспределением частиц по размерам, αm – модальный относительный размер. По этим данным рассчитали значения характеристической функции υμ, а также оценили параметры систем μ и αm, при которых волновая экспонента nμ принимает в принципе любое заданное значение nμ = f [192]. Для этого определили координаты максимума зависимости F/αmf по соотношению:

207

Для расчёта координат максимума зависимости F/αmf при фиксированных μ = 1,5, 10, 15 и 29 для заданной величины nμ (с подробным шагом Δnμ = 0,25 в диапазоне -0,5 ≤ nμ ≤ 3) применили кубическое интерполирование табличных данных [192]. Пересчёт значения параметра αm в αλ проводили по формуле их взаимосвязи (гаммараспределение), приведённой в работе [192]. Экспериментальным обоснованием корректности аналитического сглаживания осциллирующих монодисперсных калибровок n(α,m) служат экспериментальные данные, которые получены в работе [192] обработкой спектров мутности в диапазоне 0,5 ≤ λ ≤ 1,05 мкм для частиц суспензии мастикса с параметрами полидисперсности гамма – распределения μ ≈ 250 и m = 1,15 (среднее значение исследуемого нами интервала 1,01 ≤ m ≤ 1,33). Рис. 7.6 показывает, что экспериментальные данные (см. тёмные кружки) в пределах ± 2,3% в широком интервале 10 < α < 20 закономерно группируются возле аппроксимационной кривой n(α) для m = 1,15 (см. формулы (7.27)-(7.29)), сглаживающей аналитически осцилляции точных значений n(α,m).

Полученные экспериментальные и расчётные данные показывают (рис. 7.2- 7.12), что осцилляции монодисперсных характеристических функций светорассеяния [192] эффективно сглаживаются при переходе к реальным полидисперсным системам частиц с относительным показателем преломления 1,01 ≤ m ≤ 1,33. Поэтому для анализа реальных полидисперсных систем с параметрами полидисперсности по крайней мере в интервале 10 ≤ 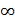μ ≤ (μ = 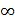– идеально монодисперсные частицы)

[249а, 250а], целесообразно использовать аппроксимационные формулы (7.18)-(7.21) и (7.27)-(7.29) как характеристические функции светорассеяния полидисперсных систем К(α,m), g(α,m), υ(α,m) и n(α,m) в наиболее важном практическом диапазоне изменения 1,01 ≤ m ≤ 1,33 и -2 ≤ n ≤ 4 для аналитического варианта решения обратных коллоидно-оптических задач методом спектра мутности и СТТ.

Для графического варианта решения обратных задач методом спектра мутности при физико-химическом анализе широкого круга дисперсных систем, в частности полимерных дисперсных систем, образующихся при СТТ растворов полимеров, вместо осциллирующих табличных данных [192] нами рассчитаны таблицы гладких характеристических функций светорассеяния полидисперсных систем. Как в таблицах [192], диапазон значений 1,01 ≤ m ≤ 1,33 и -2 ≤ n ≤ 4 охватывает все типичные полимерные и биологические дисперсные системы, а выбор шагов расчёта Δm и Δα продиктован практикой исследования таких систем методом спектра мутности и СТТ

[192, 193].

Для экспресс-анализа (особенно при одновременной вариации m и α от состава дисперсионной среды при различных значениях показателей преломления растворителя и осадителя) разработаны алгоритм и компьютерная программа обработки экспериментальных данных СТТ растворов полимеров.

Следующей важной методологической проблемой метода СТТ растворов полимеров является анализ устойчивости обратной задачи (определение Мγ,т) к влиянию дисперсии показателя преломления полимерной частицы μ3 = μ3(λ) и дисперсионной среды μ0 = μ0(λ) или m = μ3/μ0 = m(λ)). Актуальность этой проблемы определяется тем, что зачастую схемы решения обратных задач светорассеяния оказываются некорректными [192, 193].

208

В работе [251а] проведён анализ устойчивости метода СТТ к влиянию дисперсии m(λ), обусловленный составляющей систематической погрешности размера частиц n = (∂n/∂α)•Δα. На модельной системе – поли-α- метилстирол+циклогексан+октанол показана достаточно высокая устойчивость метода СТТ к влиянию дисперсии μ1 (λ) и μ0 (λ).

Далее рассмотрим коллоидно-оптические и термодинамические проблемы метода СТТ и их решения.

При «оптическом взвешивании» концентрации осаждённого полимера методом СТТ изменением температуры Т в бинарной системе полимер – растворитель (П+Р) или объёмной доли осадителя γ в тройной системе полимер – растворитель – осадитель (П+Р+О) измеряют оптическую плотности D=D(λ) или спектр мутности коллоидно-дисперсной системы частиц полимера, которую с учётом разбавления системы и длины кюветы Ɩ пересчитывают в мутность

и по формуле (7.14) рассчитывают концентрацию осаждённого полимера Мγ,т (T,γ), где объёмная доля осадителя

где Vос – объем осадителя; Vр – начальный объем раствора полимера. При исходной концентрации полимера С зависимость

называется экспериментальной кривой осаждения, в частности, при осадительном СТТ кривая осаждения Х = Мγ (γ)/C.

На этапах СТТ по формулам (7.12) и (7.13) определяют средний размер rλ = rλ(T,γ) и числовую концентрацию N = N(T,γ) коллоидно-дисперсных частиц осаждённого полимера или структуру ансамбля дисперсных частиц полимера.

При фазовом разделении с учётом материального баланса для концентрации полимера в осадке Мγ,т (T,γ) в фазе осадка справедливо

или

где Сℓ – концентрация насыщенного раствора или растворимость полимера, которая в фазовом пространстве как совокупность конфигуративных точек имеет физический смысл левой ветви бинодали [50]. Величина Х называется степенью фазового превращения или долей осаждённого полимера в коллоидно-дисперсное состояние.

В методе СТТ количественным термодинамическим критерием полного осаждения полимера служит условие

209

где Хm - максимальная доля осаждённого полимера в конце СТТ при T = Tm или γ = γm или максимальных значениях T или γ в области насыщения экспериментальной кривой осаждения Хm= М(γ,т)m/С [1а, 50].

Анализ принципиальной возможности полного перевода полимера осадка и само теоретическое или экспериментальное получение кривой осаждения Х(T,γ) для различных систем и условий будем называть оптимизацией метода СТТ. Вопрос оптимизации приобрёл большое значение в связи с эффектом неполного осаждения, установленным именно в рамках СТТ при «оптическом взвешивании» концентрации осаждённого полимера (7.14) [1а, 192, 193], в отличие от традиционного турбидиметрического титрования по мутности [190], для которого названный эффект является не диагностируемым артефактом. Дело в том, что кривая осаждения полимера Х=Мγ (γ)/C= Х(T,γ), определяющая его растворимость, содержит количественную информацию о молекулярно-массовом распределении и химическом строении полимолекулярного полимера. Только в случае полного или 100%-ного осаждения полимера имеет смысл приступать к решению обратной термодинамической задачи – обращению кривой осаждения в явную функцию ММР.

В работе [193] проанализирован принципиальный характер неполного осаждения в рамках теории Флори-Хаггинса «единой» жидкости Скотта и показано, что неполное осаждение Хm < 100% полимолекулярного полимера имеет термодинамический характер и затрагивает его высокорастворимую или низкомолекулярную часть [1а, 193], которая Хm → 100% при увеличении исходной концентрации С полимера в растворе. Осаждение низкомолекулярной части образца полимера возможно путём подбора или растворителя для системы П+Р или пары Р+О и исходной концентрации С полимера. На практике возможность достижения 100%-ного осаждения полимера увеличением С ограничивается проявлением эффектов оптических искажений [1а, 50], снижающих измеряемое значение мутности τ (7.31) и следовательно, расчётное

значение М(γ,т)m (7.14) или Хm. В этом случае Х'm < Хm, где Х'm – кажущееся значение максимальной доли осаждённого полимера, которая в отличие от случая термодина-

мического неполного осаждения [193], является убывающей функцией фактической концентрации дисперсной фазы С* = С(1-γ) при γ > γm. Антибатная зависимость Х'm от С* не зависит от природы системы П+Р+О [1а, 193] и является универсальной характеристикой геометрии прибора и пороговая концентрация С* может быть увеличена уменьшением толщины оптического слоя или кюветы.

Анализ причин эффекта неполного осаждения и рекомендации [193] служат реальной основой оптимизации метода СТТ для достижения условия 100%-ного осаждения полимера и корректного решения обратной термодинамической задачи – обращения экспериментальной кривой осаждения в явную функцию ММР.

Решения прямой и обратной термодинамической задачи в рамках СТТ [192, 193] проведено компьютерным моделированием или «машинным» экспериментом. Авторами [192, 193] компьютерным моделированием проведён анализ менее известного в практике приближенного способа решения обратной термодинамической задачи – метода Рейнера [196], учитывающего кооперативный характер осаждения фракции полимеров на этапах суммирующего фракционирования или СТТ, и показана эффективность метода Рейнера.

Безусловно, «машинным» экспериментам присущи высокая информативность и чистота, однако окончательным критерием эффективности метода СТТ и тех или

210

иных способов анализа ММР и химической неоднородности полимеров является натуральный эксперимент для решения прикладных задач научных исследований и аналитического контроля производства полимеров. В этой связи актуальной становится экспериментальная разработка следующих методологических вопросов СТТ:

-подбор оптимальной системы Р+О и условий титрования сначала для модельных [105-110] и после для практически важных волокнообразующих полимеров (ПМФИФА и сополимера акрилонитрила) [13, 186, 187];

-устранение искажений оптических факторов, приводящих к имитации неполного осаждения при титровании растворов полимеров;

-разработка калибровочной процедуры и обращения кривой осаждения в ММР полимеров;

-разработка алгоритмов и компьютерных программ для экспресс-анализа кривой осаждения осадительного СТТ и ММР и оценка эффективности этого преобразования по данным независимых исследований; решение ряда прикладных задач путём анализа ММР.

В качестве модельного полимера для решения вопросов оптимизации метода СТТ использовали поли-α-метилстирол, полученный анионной полимеризации в ИВС РАН (г. Санкт-Петербург) (см. ниже раздел 7.2.1).

7.2.1. Модельный поли-α-метилстирол. Термодинамические и коллоиднооптические принципы оптимизации. Решение обратной термодинамической задачи преобразования кривой осаждения в явную функцию молекулярно-массового распределения

Термодинамические аспекты подбора оптимальной смеси. Прежде всего рассмотрим термодинамические аспекты подбора оптимальной смеси Р+О при СТТ растворов полимеров [253а]. Анализ кривой осаждения Х=Мγ (γ)/C проведём на основе выражения для общего параметра взаимодействия χ Флори-Хаггинса тройной системы полимер+жидкость-1+жидкость-2 от объёмной доли γ жидкости-2 и параметров парного взаимодействия χij (i, j = 1,2,3) компонентов в приближении «единой» жидкости Скотта при Т = const [1а, 193]

где параметры парного взаимодействия χ12 – жидкость-1 и жидкость-2, χ23 – жид- кость-2 и полимер и χ13 – жидкость-1 и полимер.

При условии |Δχ| = |χ23- χ13| ≤ |χ12| ≠ 0 и состава γо = 0,5- Δχ/2χ12 параметр тройной системы (7.37) имеет экстремум

при χ12 > 0 – минимум, а при χ12 < 0 – максимум. Значение γ, при котором парабола (7.37) пересекает линию χ = 0,5 (θ – условие Флори-Хаггинса [193]), отвечает составу θ – смеси: