
- •Министерство образования и науки Российской Федерации
- •Глава I. Азы теории чисел
- •§ 1. Деление целых чисел с остатком
- •5709 Mmmmmdссiiiiiiiii,
- •Перевод числа из десятичной системы счисления в q-ичную
- •Перевод числа из q-чной системы счисления в десятичную (схема Горнера)
- •Перевод числа из одной системы счисления в другую
- •Арифметические действия в позиционных системах счисления
- •§ 2. Деление целых чисел нацело
- •Свойства делимости нацело
- •§ 3. Наибольший общий делитель и наименьшее общее кратное
- •Основные свойства наибольшего общего делителя и наименьшего общего кратного
- •§ 4. Алгоритм Евклида
- •Расширенный алгоритм Евклида
- •§ 5. Взаимно простые числа
- •Простейшие свойства взаимно простых чисел
- •§ 6. Простые числа
- •Простейшие свойства простых чисел
- •§ 7. Простые числа в арифметических прогрессиях
- •О распределении простых чисел
- •§ 8. Язык сравнений
- •Свойства сравнений
- •§ 9. Функция Эйлера
- •§ 10. Теоремы Эйлера и Ферма
- •§ 11. Признаки делимости
- •§ 12. Принцип Дирихле
- •Глава II. Некоторые диофантовы уравнения
- •§ 1. Линейные диофантовы уравнения
- •§ 2. Общее диофантово уравнение от одного переменного
- •§ 5. Пифагоровы тройки
- •§ 6. Уравнение Ферма-Пелля
- •Глава III. Великая теорема ферма и abc – проблема
- •§ 1. Великая теорема Ферма
- •§ 2. Методы Эйлера-Куммера доказательства Великой теоремы Ферма
- •§ 3. Гипотеза Таниямы и доказательство Великой теоремы Ферма
- •§ 4. Abc – Теорема для многочленов и её следствия
- •§ 5. Abc – Гипотеза для натуральных чисел
- •§ 6. Некоторые следствия из abc– гипотезы
- •Глава IV. Задача о счастливых билетах
- •§ 1. Сведение задачи к задаче о числе наборов цифр с заданной суммой компонент
- •§ 2. Задача о числе наборов цифр с заданной суммой компонент
- •§ 3. Ещё одно решение задачи о числе наборов цифр с заданной суммой компонент
§ 6. Уравнение Ферма-Пелля
Так называется диофантово уравнение x2 – Ay2 = 1, где A N. Его исследование было начато П. Ферма, а окончательное описание решений получено Л. Дирихле. Дж. Пелль не имеет к решению этого уравнения никакого отношения, его имя ошибочно связал с этим уравнением Л. Эйлер.
I .
Рациональные
решения. Вначале
найдём все рациональные решения уравнения
Ферма-Пелля.
.
Рациональные
решения. Вначале
найдём все рациональные решения уравнения
Ферма-Пелля.
Кривая
с уравнением
Ферма x2
– Ay2
= 1 имеет
канонический вид
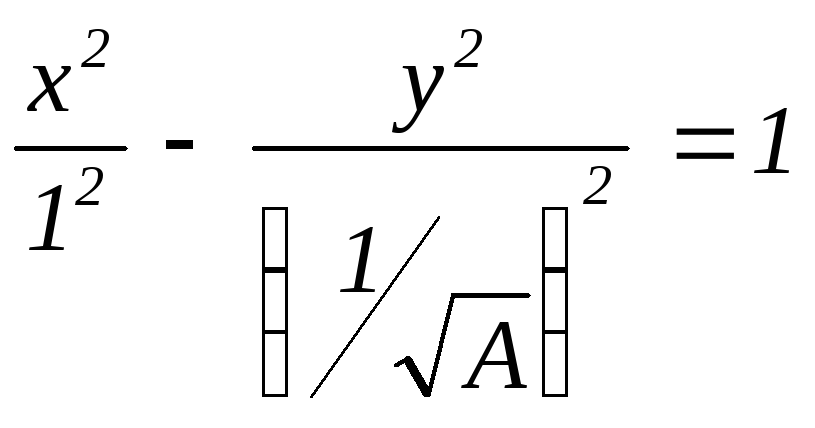 и, как известно, является гиперболой с
вершинами(±1;
0) и асимптотами
y
= ±
и, как известно, является гиперболой с
вершинами(±1;
0) и асимптотами
y
= ±
![]() x
.
x
.
Выберем на ней рациональную точку – её вершину S(1; 0), с помощью которой проведём параметризацию остальных рациональных точек этой кривой.
Если точка M(r
; s)
рациональна,
т.е. r,
s
Q
, то прямая
(MS)
имеет каноническое уравнение
![]()
y
=
y
=
![]() и угловой коэффициент k
=
и угловой коэффициент k
= ![]()
Q
.
Q
.
Обратно, если задан угловой коэффициент k Q , то можно найти все точки пересечения прямой y = k(x – 1), проходящей через точку S, с кривой x2 – Ay2 = 1 : одна из них S, а вторая находится из соотношений
x2 – Ak2(x – 1)2 = 1 (x – 1)(x + 1) = Ak2(x – 1)2
(1
– Ak2)x
= –1 – Ak2
![]() .
.
Знаменатель
последнего выражения не обращается в
ноль, если число A
не является
квадратом рационального числа: 1
– Ak2
= 0
A
=
![]() .
В случае натурального параметра A
это возможно только если A
полным квадратом. Действительно, если
.
В случае натурального параметра A
это возможно только если A
полным квадратом. Действительно, если
![]() – несократимая дробь, тоA
=
– несократимая дробь, тоA
=
![]()
Ap2
= q2
и т.к. p
и q
взаимно
просты, то A
= mq,
mp2
= q,
а значит, m
= qs,
sp2
= 1 и s
= 1, p
= ±1, а A
= q2.
Ap2
= q2
и т.к. p
и q
взаимно
просты, то A
= mq,
mp2
= q,
а значит, m
= qs,
sp2
= 1 и s
= 1, p
= ±1, а A
= q2.
Теорема (о рациональных решениях уравнения Ферма-Пелля). Все рациональные точки кривой x2 – Ay2 = 1 (A N) имеют вид M(x ; y), где
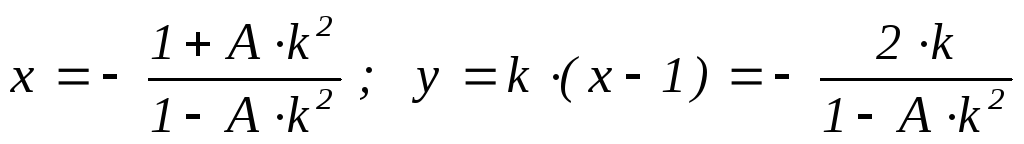 (k
Q),
если A
не является полным квадратом;
(k
Q),
если A
не является полным квадратом;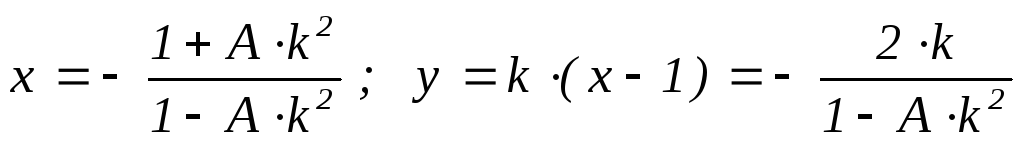 (k
Q
\ {
(k
Q
\ { }),
если
A
= B2
;
}),
если
A
= B2
;
II. Целочисленные решения. Теперь рассмотрим целочисленные решения уравнения Ферма. Прежде всего, заметим, что имеет смысл рассматривать только уравнения, в которых A не является полным квадратом: если A = B2, то
x2 – Ay2 = 1 x2 – B2y2 = 1 (x + By)(x – By) = 1
![]()
![]() .
.
Такие решения назовём тривиальными.
1. Арифметика
чисел x
+
![]() y
(x,
y
Z).
Левая часть уравнения Ферма-Пелля
разложима на множители: x2
– Ay2
= (x
+
y
(x,
y
Z).
Левая часть уравнения Ферма-Пелля
разложима на множители: x2
– Ay2
= (x
+
![]() y)(x
–
y)(x
–
![]() y).
Поэтому числа вида x
+
y).
Поэтому числа вида x
+
![]() y,
где x,
y
Z
, играют важную роль в исследовании
решений этого уравнения. Обозначим
y,
где x,
y
Z
, играют важную роль в исследовании
решений этого уравнения. Обозначим
K
= {x
+
![]() y
R
| x,
y
Z}.
y
R
| x,
y
Z}.
В дальнейшем будем
отождествлять решение (x;
y)
этого
диофантова уравнения с числом x
+
![]() y.
y.
Для любого числа
x
+
![]() y
определим норму
N(x
+
y
определим норму
N(x
+
![]() y)
= x2
– Ay2.
y)
= x2
– Ay2.
Следующие формулы показывают, что множество рассматриваемых чисел замкнуто относительно сложения, вычитания, умножения, оно содержит 0 и 1, –1:
(x +
![]() y)
+ (z +
y)
+ (z +
![]() t)
= (x + z) +
t)
= (x + z) +
![]() (y
+ t),
(y
+ t),
(x +
![]() y)
– (z +
y)
– (z +
![]() t)
= (x – z) +
t)
= (x – z) +
![]() (y
– t),
(y
– t),
(x +
![]() y)(z
+
y)(z
+
![]() t)
= (xz
+ Ayt)
+
t)
= (xz
+ Ayt)
+
![]() (xt
+ yz),
(xt
+ yz),
0 = 0 +
![]() 0,
1 = 1 +
0,
1 = 1 +
![]() 0,
–1 = –1 +
0,
–1 = –1 +
![]() 0.
0.
Для двух чисел x
+
![]() y,
z
+
y,
z
+
![]() t
K
можно
вычислить их частное
t
K
можно
вычислить их частное
![]() ,
,
которое не
обязательно принадлежит K.
Однако это частное принадлежит K,
если xz
– Ayt
z2
– At2
и –xt
+ yz
z2
– At2.
Эти условия выполняются, например, в
случае N(z
+
![]() t)
= z2
– At2
= ±1.
t)
= z2
– At2
= ±1.
Для числа
= x
+
![]() y
K
определим
y
K
определим
![]() = x
–
= x
–
![]() y
K
– сопряжённое
число к
. Легко проверить следующие свойства
сопряжённых чисел:
y
K
– сопряжённое
число к
. Легко проверить следующие свойства
сопряжённых чисел:
![]() ,
,
![]() ,
,
![]() ,
,
N(±1) = 1, N(0) = 0.
Кроме того, норма от произведения чисел равно произведению норм:
N()
= ()![]() = ()(
= ()(![]() )
=
)
= ![]()
![]() = N()N().
= N()N().
Ясно, что решения уравнения Ферма-Пелля имеют единичную норму. Значит, множество решений замкнуто относительно умножения и деления.
2. Приближение действительных чисел рациональными. Напомним лемму, доказанную ранее с помощью принципа Дирихле.
Лемма (о
приближении действительных чисел
рациональными).
Для любого действительного числа r
> 0 и произвольного n
N
найдутся такие натуральные числа a,
b
N,
где 1
b
n,
что |br
– a|
![]()
![]() .
.
Будем использовать
её для r
=
![]() .
.
3. Существование решения уравнения Ферма-Пелля. Докажем, что при любом A N диофантово уравнение x2 – Ay2 = 1 имеет нетривиальное решение, в котором y 0.
Зафиксируем
произвольное n
N
и, пользуясь доказанной леммой, найдём
an
Z
и 1
bn
< n
со свойством
|an
–
![]() bn|
<
bn|
<
![]() . Тогда
. Тогда
|an2
– Abn2|
= |an
–
![]() bn||an
+
bn||an
+
![]() bn|
<
bn|
<
![]() |(an
–
|(an
–
![]() bn)
+ 2
bn)
+ 2![]() bn|
bn|
![]() (|an
–
(|an
–
![]() bn|
+2|bn|
bn|
+2|bn|![]() )
<
)
<![]() (
(![]() + 2n
+ 2n![]() )
= 2
)
= 2![]() +
+![]()
2
2![]() + 1.
+ 1.
Поэтому натуральная
величина |an2
– Abn2|
принимает
лишь конечное число значений на парах
(an
; bn)
при n
N.
Количество таких пар бесконечно, т.к.
величина |an
–
![]() bn|
<
bn|
<
![]() стремится
к нулю при n
и не может
быть равной нулю, поскольку
стремится
к нулю при n
и не может
быть равной нулю, поскольку
![]() иррационален.
По принципу Дирихле получаем, что
некоторое значение c
величины
|an2
– Abn2|
принимается
бесконечное число раз. Пусть M
= {(a;
b)
Z2
| |a2
– Ab2|
= с} – бесконечное
множество. Если c
= 1, то всё
доказано: при a2
– Ab2
= – 1 квадрат
(a
+
иррационален.
По принципу Дирихле получаем, что
некоторое значение c
величины
|an2
– Abn2|
принимается
бесконечное число раз. Пусть M
= {(a;
b)
Z2
| |a2
– Ab2|
= с} – бесконечное
множество. Если c
= 1, то всё
доказано: при a2
– Ab2
= – 1 квадрат
(a
+
![]() b)2
= (a2
+ Ab2)
+ 2ab
b)2
= (a2
+ Ab2)
+ 2ab![]() будет
решением, т.к. N(2)
= N()2.
будет
решением, т.к. N(2)
= N()2.
Поскольку множество
M
бесконечно,
а множество остатков при делении на c
конечно, то
найдутся две такие различные пары (a1
; b1),
(a2
; b2)
M,
что |a12
– Ab12|
= c
= |a22
– Ab22|
и a1
a2
, b1
b2
(mod
c).
Для доказательства достаточно по
принципу Дирихле раскладывать пары
(a;
b)
M
по кучам
(r;
s)
– всем парам
остатков от деления на c
(0
![]()
c).
c).
Поскольку знаки
чисел x,
y
в решении
x
+ y![]() можно менять произвольно, будем считать,
что ai
> 0, bi
> 0 (i
= 1, 2).
можно менять произвольно, будем считать,
что ai
> 0, bi
> 0 (i
= 1, 2).
Теперь получаем
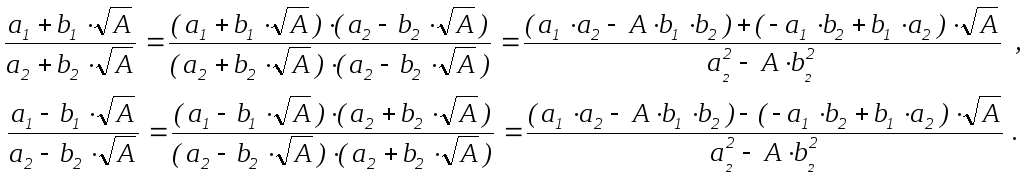
Поскольку a22 – Ab22 = c и a1 a2 , b1 b2 (mod c), то a1a2 – Ab1b2 a12 – Ab12 = c 0, –a1b2 + b1a2 –a1b1 + b1a1 = 0 (mod c).
Поэтому числа 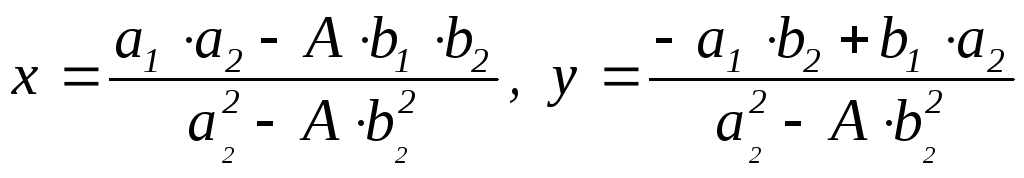
Z,
причём
Z,
причём
x2
– Ay2
= (x
+ y![]() )(x
– y
)(x
– y![]() )
=
)
=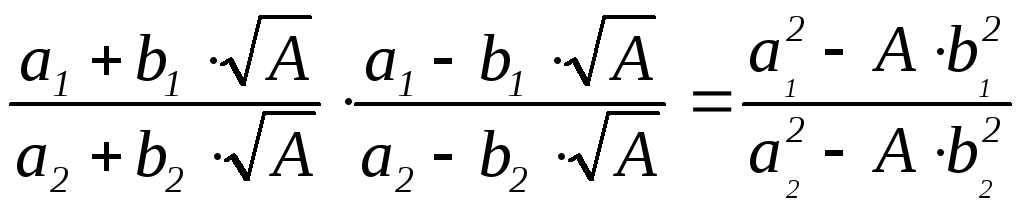 = ±1.
= ±1.
При этом y
0: если y
= 0, то
x
= ±1 = x
+ y![]() =
=![]() , т.е. вопреки выбору получаем (a1
; b1)
= (a2
; b2).
, т.е. вопреки выбору получаем (a1
; b1)
= (a2
; b2).
Найденное
нетривиальное решение
= x
+ y![]() порождает
бесконечную серию решений
n
(n
Z),
которые все различны как степени числа,
не равного по модулю единице.
порождает
бесконечную серию решений
n
(n
Z),
которые все различны как степени числа,
не равного по модулю единице.
Итак, доказана
Теорема (о существовании нетривиальных решений уравнения Ферма-Пелля). Уравнение Ферма-Пелля x2 – Ay2 = 1 имеет бесконечное количество нетривиальных решений.
4. Структура
решений.
Ясно, что
если x
+ y![]() –решение,
то числа (–x)
+ y
–решение,
то числа (–x)
+ y![]() ,x
+ (–y)
,x
+ (–y)![]() ,
(–x)
+ (–y)
,
(–x)
+ (–y)![]() тоже являются
решениями. Поэтому с любым нетривиальным
решением, у которого y
0, уравнение
Ферма-Пелля имеет и положительное
решение, у которого x
> 0, y
> 0.
Положительное решение x0
+ y0
тоже являются
решениями. Поэтому с любым нетривиальным
решением, у которого y
0, уравнение
Ферма-Пелля имеет и положительное
решение, у которого x
> 0, y
> 0.
Положительное решение x0
+ y0![]() с наименьшим
значением x
во множестве
всех положительных решений назовём
основным.
с наименьшим
значением x
во множестве
всех положительных решений назовём
основным.
На самом деле 1
+
![]() <x0
+ y0
<x0
+ y0![]()
x
+ y
x
+ y![]() для каждого
положительного решения x
+ y
для каждого
положительного решения x
+ y![]() .
Действительно, неравенство 1+
.
Действительно, неравенство 1+![]() <x0+y0
<x0+y0![]() очевидно.
Второе неравенство следует из минимальности
x0
и соотношений x2
– Ay2
= 1 = x02
– Ay02
: 0
x2
– x02
= A(y2
– y02),
т.е. y
y0
, x
x0
и потому x0
+ y0
очевидно.
Второе неравенство следует из минимальности
x0
и соотношений x2
– Ay2
= 1 = x02
– Ay02
: 0
x2
– x02
= A(y2
– y02),
т.е. y
y0
, x
x0
и потому x0
+ y0![]()
x
+ y
x
+ y![]() .
Итак, величина основного решения
минимальна.
.
Итак, величина основного решения
минимальна.
Теорема (о структуре решений уравнения Ферма-Пелля). Любое решение уравнения Ферма-Пелля является с точностью до знака степенью (положительной или отрицательной) основного решения.
Доказательство.
Во-первых, как уже отмечалось выше,
множество решений замкнуто относительно
умножения и деления. Поэтому, если
= x0
+ y0![]() –основное
решение, то все его степени тоже
n
(n
Z)
будут тоже
решениями.
–основное
решение, то все его степени тоже
n
(n
Z)
будут тоже
решениями.
Рассмотрим теперь
степени
,
2 , … ,
n
, … основного
решения. Ясно, что
> 1 и поэтому
n
при n
. Если
= x
+ y![]() –положительное
решение (x,
y
> 0), не
равное никакой степени
n
(n
N),
то найдётся однозначно определённое
n
N
со свойством
k
<
<
k+1.
Тогда
получаем решение
=
–положительное
решение (x,
y
> 0), не
равное никакой степени
n
(n
N),
то найдётся однозначно определённое
n
N
со свойством
k
<
<
k+1.
Тогда
получаем решение
=
![]() , причём1 <
=
, причём1 <
=
![]() <
, что
невозможно.
<
, что
невозможно.
Итак, каждое
положительное решение является степенью
основного. Пусть теперь
= x
+ y![]() –произвольное
нетривиальное неположительное решение.
Рассмотрим три возможных случая:
–произвольное
нетривиальное неположительное решение.
Рассмотрим три возможных случая:
1. x
> 0, y
< 0. Тогда
![]() =x
– y
=x
– y![]() –положительное
решение, так что
–положительное
решение, так что
![]() =
n
и
=
=
n
и
=
![]() .
.
2. x
< 0, y
< 0. Тогда
–
= (–x)
+ (–y)![]() –положительное
решение, и поэтому –
=
n
,
= –
n
.
–положительное
решение, и поэтому –
=
n
,
= –
n
.
3. x < 0, y > 0. Тогда – удовлетворяет случаю 1, так что – = –n и = – –n.
Теорема доказана.
