
- •Министерство образования и науки Российской Федерации
- •Глава I. Азы теории чисел
- •§ 1. Деление целых чисел с остатком
- •5709 Mmmmmdссiiiiiiiii,
- •Перевод числа из десятичной системы счисления в q-ичную
- •Перевод числа из q-чной системы счисления в десятичную (схема Горнера)
- •Перевод числа из одной системы счисления в другую
- •Арифметические действия в позиционных системах счисления
- •§ 2. Деление целых чисел нацело
- •Свойства делимости нацело
- •§ 3. Наибольший общий делитель и наименьшее общее кратное
- •Основные свойства наибольшего общего делителя и наименьшего общего кратного
- •§ 4. Алгоритм Евклида
- •Расширенный алгоритм Евклида
- •§ 5. Взаимно простые числа
- •Простейшие свойства взаимно простых чисел
- •§ 6. Простые числа
- •Простейшие свойства простых чисел
- •§ 7. Простые числа в арифметических прогрессиях
- •О распределении простых чисел
- •§ 8. Язык сравнений
- •Свойства сравнений
- •§ 9. Функция Эйлера
- •§ 10. Теоремы Эйлера и Ферма
- •§ 11. Признаки делимости
- •§ 12. Принцип Дирихле
- •Глава II. Некоторые диофантовы уравнения
- •§ 1. Линейные диофантовы уравнения
- •§ 2. Общее диофантово уравнение от одного переменного
- •§ 5. Пифагоровы тройки
- •§ 6. Уравнение Ферма-Пелля
- •Глава III. Великая теорема ферма и abc – проблема
- •§ 1. Великая теорема Ферма
- •§ 2. Методы Эйлера-Куммера доказательства Великой теоремы Ферма
- •§ 3. Гипотеза Таниямы и доказательство Великой теоремы Ферма
- •§ 4. Abc – Теорема для многочленов и её следствия
- •§ 5. Abc – Гипотеза для натуральных чисел
- •§ 6. Некоторые следствия из abc– гипотезы
- •Глава IV. Задача о счастливых билетах
- •§ 1. Сведение задачи к задаче о числе наборов цифр с заданной суммой компонент
- •§ 2. Задача о числе наборов цифр с заданной суммой компонент
- •§ 3. Ещё одно решение задачи о числе наборов цифр с заданной суммой компонент
§ 6. Некоторые следствия из abc– гипотезы
1. Великая теорема Ферма. Диофантово уравнение xn + yn = zn не имеет натуральных решений x, y, z N при n > 2.
Доказательство. От противного: пусть xn + yn = zn для некоторых натуральных чисел x, y, z и n > 2. Можно считать, что НОД(x, y) = 1. Действительно, если простое число p является общим делителем x и y, то p | xn, p | yn, и значит, p | zn, а значит, по свойству простых чисел, p | z, так что равенство xn + yn = zn можно сократить на pn, где p | НОД(x, y), получив аналогичное равенство x1n + y1n = z1n. Здесь x1 = x / p, y1 = y / p, z1 = z / p и НОД(x1 , y1) = НОД(x, y) / p < НОД(x, y). Выполняя описанную процедуру несколько раз, придём к соотношению xkn + ykn = zkn со взаимно простыми натуральными числами xk , yk .
Итак, пусть xn + yn = zn и НОД(x, y) = 1. Тогда, числа xn и yn тоже взаимно просты, и обозначив a = xn, b = yn , c = zn получим abc-тройку, для которой, согласно (abc)-гипотезе, выполняется цепочка неравенств:
zn = c < r(abc)2 = r(xnynzn)2 = r(xyz)2 (xyz)2 < (z3)2 = z6 .
Значит, n < 6, что противоречит давно доказанным случаям Великой теоремы Ферма для n = 3, 4, 5.
Теорема доказана.
В этом доказательстве использована (abc)-гипотеза. Если же пользоваться abc-гипотезой, то можно доказать справедливость Великой теоремы Ферма, начиная с некоторого показателя n. Действительно, согласно abc-гипотезе (см. теорему об её эквивалентных формулировках в прошлом параграфе) найдётся такое h > 1, что для любой abc-тройки верно неравенство c < r(a, b, c)h. Тогда, как и в приведённом выше доказательстве,
zn = c < r(abc)h = r(xnynzn)h = r(xyz)h (xyz)h < (z3)h = z3h .
Значит, равенство xn + yn = zn может иметь место только при n < 3h, что и утверждалось.
2. Уравнение Ферма-Каталана xk + ym = zn (2 k m n). Это уравнение обобщает диофантово уравнение Ферма xn + yn = zn на случай произвольных натуральных показателей.
При исследовании этого уравнения различают три случая:
а)
![]() ,б)
,б)
![]() ,в)
,в)
![]() .
.
Если в третьем
случае неравенство выполнено для многих
значений k,
m,
n,
то первые два случая накладывают на
эти значения серьёзные ограничения.
Неравенство
![]() ,
очевидно, равносильноmn
+ kn
+ km
kmn,
левая часть которого не превосходит
3mn,
что даёт ограничение k
3, т.е. k
= 2 или k
= 3. Если k
= 2, то 2(m
+ n)
mn
(m
– 2)(n
– 2)
4, т.е. либо
m
= 2, n
2, либо m
= 3, n
6. Если же
k
= 3, то
3(m
+ n)
2mn,
и левая часть не больше 6n,
а значит, m
3, т.е. m
= 3
(m
k = 3)
и n
= 3.
,
очевидно, равносильноmn
+ kn
+ km
kmn,
левая часть которого не превосходит
3mn,
что даёт ограничение k
3, т.е. k
= 2 или k
= 3. Если k
= 2, то 2(m
+ n)
mn
(m
– 2)(n
– 2)
4, т.е. либо
m
= 2, n
2, либо m
= 3, n
6. Если же
k
= 3, то
3(m
+ n)
2mn,
и левая часть не больше 6n,
а значит, m
3, т.е. m
= 3
(m
k = 3)
и n
= 3.
Итак, случаи а), б) имеют следующие описания:
а)
![]()
(k;
m;
n)
{(2; 2; n),
(2; 3; 3), (2; 3; 4),
(2; 3;
5)};
(k;
m;
n)
{(2; 2; n),
(2; 3; 3), (2; 3; 4),
(2; 3;
5)};
б)
![]()
(k;
m;
n)
{(3;
3;
3),
(2; 4;
4),
(2; 3; 6)}.
(k;
m;
n)
{(3;
3;
3),
(2; 4;
4),
(2; 3; 6)}.
Оказывается, что в случае а) каждое диофантово уравнение xk + ym = zn имеет бесконечное число решений. Для того чтобы в этом убедиться, нужно для каждой из выписанных троек степеней построить бесконечную серию решений. Например, для уравнения x2 + y2 = z2s+1 с нечётным значением n = 2s + 1 можно взять x = a(a2 + b2)s, y = b(a2 + b2)s, z = a2 + b2 (a, b Z). Для чётного n = 2s решения можно строить последовательно: если для уравнения x2 + y2 = zs уже построена бесконечная серия (xp ; yp ; zp)p N решений, то для уравнения x2 + y2 = z2s можно взять
x = 2xpyp , y = xp2 – yp2, z = zp .
Для случая б) доказано, что каждое диофантово уравнение xk + ym = zn имеет лишь конечное число взаимно простых решений (НОД(x, y, z) = 1). Например, уравнение x3 + y3 = z3 – это уравнение Ферма и не имеет натуральных решений. Уравнение x2 + y4 = z4 исследуется аналогично уравнению x4 + y4 = z2 при доказательстве теоремы Ферма для показателя 4.
В случае в) из abc-гипотезы можно вывести следующую теорему:
Теорема. Существует лишь конечное число наборов (xk ; ym ; zn) со свойствами:
x, y, z
N;
НОД(x,
y, z) = 1; xk
+ ym
= zn
;
![]() ;
k, m, n
2 .
;
k, m, n
2 .
Доказательство. Любой набор (xk ; ym ; zn) определяет abc-тройку с a = xk , b = ym , c = zn , причём
r(abc) = r(xkymzn) = r(x)r(y)r(z) xyz = (xk)1 / k(ym)1 / m(zn)1 / n =
= a1 / kb1 / mc1 / n < c1 / kc1 / mc1 / n = c1 / h,
где
h
=
![]() . Поэтому
c
> r(abc)h,
т.е. любой рассматриваемый набор
определяет хитовую abc-тройку
с мерой
хитовости больше h.
По abc-гипотезе
таких троек лишь конечное число.
. Поэтому
c
> r(abc)h,
т.е. любой рассматриваемый набор
определяет хитовую abc-тройку
с мерой
хитовости больше h.
По abc-гипотезе
таких троек лишь конечное число.
Теорема доказана.
В 1995 г. без использования abc-гипотезы была доказана следующая теорема Х. Дармона и А. Гранвилля (Darmon H., Granville A. On the equations zm = F(x,y) and Axp + Byq = Czr. Bull. Lond. Math. Soc. 27, No.6, 513-543 (1995)):
Теорема.
Для любого
набора (k
; m
; n)
со свойствами
![]() ;
k,
m,
n
2 диофантово уравнение xk
+ ym
= zn
имеет лишь конечное число решений.
;
k,
m,
n
2 диофантово уравнение xk
+ ym
= zn
имеет лишь конечное число решений.
Ясно, что утверждение, выведенное выше с использованием abc-гипотезы, значительно сильнее: оно утверждает глобальную конечность наборов, в отличие от конечности числа решений каждого уравнения.
В частности, доказана и гипотеза Каталана: диофантово уравнение Каталана 1 + ym = zn имеет лишь конечное число решений. Ранее эта гипотеза была доказана без использования abc-техники Преда Михайлеску (Preda Mihăilescu Primary cyclotomic units and a proof of Catalan's conjecture, J. Reine Angew. Math. 572 (2004), 167–195).
Следует отметить, что на сегодняшний день известны лишь следующие решения уравнения xk + ym = zn :
1k + 23 = 32, 132 + 73 = 29, 27 + 173 = 712, 25 +72 = 34, 35 +114 = 1222,
177 +762713 = 210639282, 14143 + 22134592 = 657, 338 + 15490342 = 156133
438 + 962223 = 300429072, 92623 + 153122832 = 1137.
3. Гипотеза Морделла (1922 г.). Пусть задан многочлен f(x, y) степени n > 1 от двух переменных x, y с комплексными коэффициентами. Тогда алгебраическое уравнение f(x, y) = 0 задаёт алгебраическую кривую, которую можно превратить (путём некоторой компактификации) в риманово многообразие и рассмотреть род g этого многообразия. Долгое время оставалась недоказанной следующая гипотеза Морделла: если g 2, то на рассматриваемой кривой с уравнением f(x, y) = 0 лишь конечное число рациональных точек, т.е. точек с рациональными координатами (Mordell L. J. On the rational solutions of the indeterminate equations of the third and fourth degrees. Cambr. Phil. Soc. Proc. 21, 179—192 (1922)).
Особо важен случай
гладкой
кривой :
кривая с уравнением
f(x,
y)
= 0 называется
гладкой,
если система алгебраических уравнений
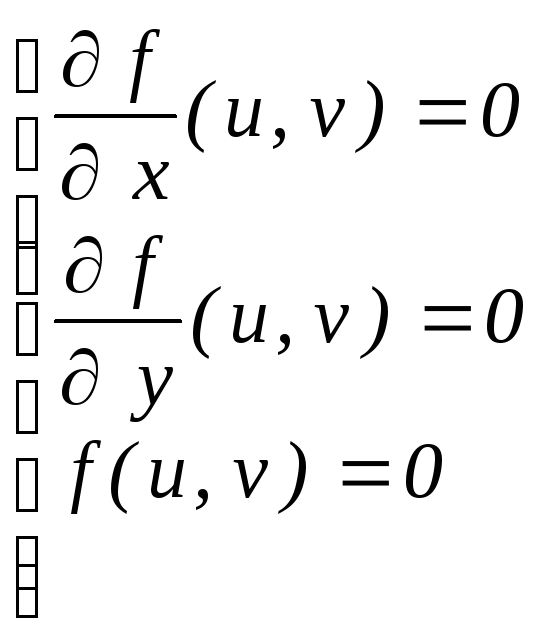 нет решений. В этом случае род кривой
вычисляется просто:g
=
нет решений. В этом случае род кривой
вычисляется просто:g
=
![]() . Таким
образом, проверка конечности числа
рациональных точек превращается с
помощью гипотезы Морделла в чисто
алгебраическое упражнение.
. Таким
образом, проверка конечности числа
рациональных точек превращается с
помощью гипотезы Морделла в чисто
алгебраическое упражнение.
Примеры:
1.
Для кривой с уравнением xn
+ yn
= 1, которая
тесно связана с уравнением Ферма xn
+ yn
= zn,
имеем f(x,
y)
= xn
+ yn
– 1
и система
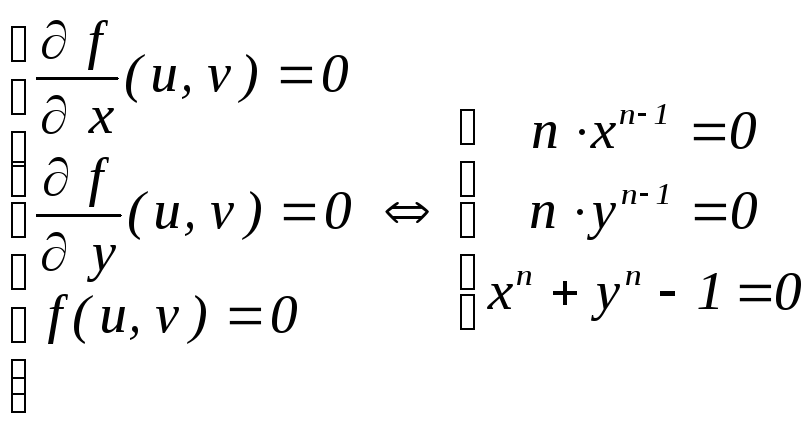 не
имеет решений. Таким образом, кривая
гладкая, её родg
=
не
имеет решений. Таким образом, кривая
гладкая, её родg
=
![]() > 2 при n
> 2, так что
на ней лежит лишь конечное число
рациональных точек. Отсюда легко
вывести, что уравнение Ферма имеет не
более конечного числа взаимно простых
нетривиальных решений.
> 2 при n
> 2, так что
на ней лежит лишь конечное число
рациональных точек. Отсюда легко
вывести, что уравнение Ферма имеет не
более конечного числа взаимно простых
нетривиальных решений.
2.
Кривая с уравнением x2
+ y2
= 1 гладкая,
но её род g
= 1, так что
не удивительно, что на ней лежит бесконечно
много рациональных точек
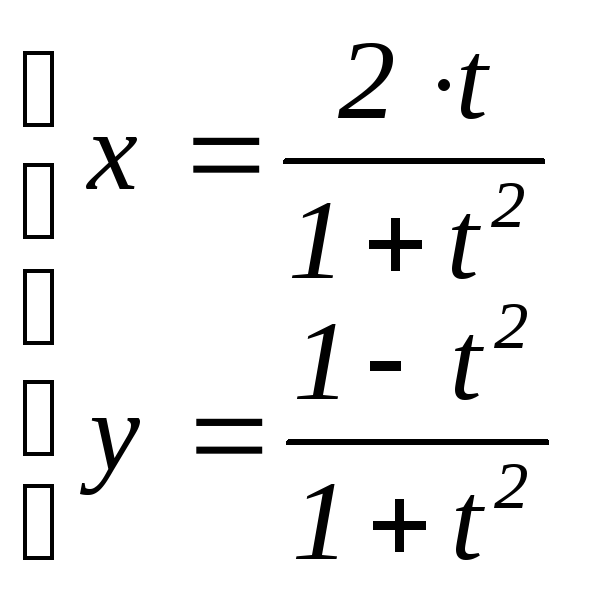 (t
R).
(t
R).
3.
Кривая с уравнением x
+ y
= 2 гладкая,
но её род g
= 0, на ней
лежит бесконечно много рациональных
точек
![]() (t
R).
(t
R).
4. Кривая с уравнением x + y = 0 не гладкая (?!). На ней бесконечно много рациональных точек.
Гипотеза Морделла была доказана Г. Фалтингсом в 1984 г. ещё до появления abc-гипотезы (Faltings G. Die Vermutungen von Tate und Mordell // Jahresber. Deutsch. Math.-Verein. 86 (1984), no. 1, 1—13.). Это был революционный прорыв в изучении алгебраических кривых.
В 1991 г. Ноам Элкис доказал, что гипотеза Морделла следует из abc-гипотезы. Более того, с её помощью можно получить эффективные оценки высоты рациональных точек на алгебраических кривых (Elkies Noam D. abc implies Mordell. Int. Math. Res. Not. 1991, No.7, 99-109 (1991)).
4.
Диофантово
уравнение
pv
– pw
= qx
– qy
имеет лишь конечное число решений.
Здесь p,
q
– различные
простые числа, v,
x,
w,
y
N.
В
2003 г.
Флориан
Люка (Luca)
показал, что из abc-гипотезы
следует конечность числа наборов (p;
q;
v;
w;
x;
y),
удовлетворяющих этому уравнению (Luca
F. On the Diophantine equation
![]() // Indag.
Math.,
New
Ser.
14, No.
2, 207-222
(2003)).
// Indag.
Math.,
New
Ser.
14, No.
2, 207-222
(2003)).
5.
Теорема
Туэ-Зигеля-Рота.
В 1955 г. Клаусом Ротом (Klaus
Roth)
была доказана следующая теорема:
для любого
алгебраического числа
и
> 2 неравенство
![]() имеет лишь конечное число несократимых
решений
имеет лишь конечное число несократимых
решений ![]() . Эта теорема придала окончательную
форму исследованиям, начатым в своё
время Дирихле, Туэ и Зигелем.
. Эта теорема придала окончательную
форму исследованиям, начатым в своё
время Дирихле, Туэ и Зигелем.
В 1994 г. Энрико
Бомбьери доказал, что эта мощная теорема
является следствием abc-гипотезы
(Bombieri,
E.
Roth's
theorem and the abc conjecture // preprint (1994), см.
также
van Frankenhuysen M. The abc conjecture implies Roth's theorem and
Mordell's conjecture // Math. Contemporanea,
76, 45-72 (1999)). Он получил и эффективную
оценку: для любого алгебраического
числа
существует
такая константа C
= C(),
что неравенство
![]() выполнено
при k
C()(ln
n)
–1 / 2
(ln
(ln
n))
–1.
выполнено
при k
C()(ln
n)
–1 / 2
(ln
(ln
n))
–1.
6. Проблема Брокарда (Brocard): Какие решения имеет диофантово уравнение n ! + 1 = m2 ? Его решения называются парами Брауна (Brown). Очевидно, что решения есть: n = 4, m = 5; n = 5, m = 11; n = 7, m = 71. Есть ли другие решения ?
С помощью abc-гипотезы удалось доказать, что это диофантово уравнение имеет лишь конечное число решений, т.е. пар Брауна лишь конечное число (см. Nitaj, Abderrahmane La conjecture abc. (The abc conjecture) // Enseign. Math., II. Ser. 42, No.1-2, 3-24 (1996), Overholt, Marius The diophantine equation n! + 1 = m2 // Bull. Lond. Math. Soc. 25, No.2, 104 (1993), Dabrowski, Andrzej On the diophantine equation x! + A = y2 // Nieuw Arch. Wiskd., IV. Ser. 14, No. 3, 321-324 (1996)).
7. Простые числа Вифериха (Wieferich). Простое число p называется простым числом Вифериха, если p2 делит 2p – 1 – 1. Эти числа, как ни странно, возникали при доказательствах Великой теоремы Ферма, но их довольно мало: среди простых чисел меньших 4.000.000.000.000, всего два числа Вифериха – 1093 и 3511. Отметим, что p | 2p – 1 – 1 для любого нечётного p ввиду малой теоремы Ферма.
В 1988 г. Джозефом Сильверманом (Silverman) было доказано, что abc-гипотеза подтверждает наличие “малого” количества простых чисел Вифериха: для любого a N существует бесконечно много простых чисел p со свойством p2 не делит a p – 1 – 1 (Silverman, Joseph H. Wieferich's criterion and the abc-conjecture // J. Number Theory 30, No. 2, 226-237 (1988)).
8.
Слабая
гипотеза Маршалла Холла:
Для любого
> 0 существует такая константа С()
> 0, что если x3
y2
для натуральных x
и y,
то |x3
– y2|>
C()max(x3,
y2)![]() (Nitaj,
Abderrahmane
La
conjecture
abc.
(The
abc conjecture) // Enseign. Math., II. Ser. 42, No.1-2, 3-24
(1996), см.
также
Schmidt, Wolfgang M. Diophantine approximations and diophantine
equations // Lecture Notes in Mathematics. 1467. Berlin etc.:
Springer-Verlag. viii, 217 p. (1991)).
(Nitaj,
Abderrahmane
La
conjecture
abc.
(The
abc conjecture) // Enseign. Math., II. Ser. 42, No.1-2, 3-24
(1996), см.
также
Schmidt, Wolfgang M. Diophantine approximations and diophantine
equations // Lecture Notes in Mathematics. 1467. Berlin etc.:
Springer-Verlag. viii, 217 p. (1991)).
9. Гипотеза Эрдёша (Erdös) о последовательных степенных целых числах. Натуральное число называется степенным, если любое простое число участвует в его каноническом разложении с показателем 2 или выше. Нетрудно понять, что любое степенное число представимо в виде A2B3 для некоторых натуральных A, B. Гипотеза Эрдёша предполагает, что не существует трёх последовательных степенных чисел.
a·b·c-гипотеза позволяет доказать более слабое утверждение: множество троек последовательных степенных чисел конечно.
Можно доказать, что конечно и множество степенных троек, являющихся последовательными членами арифметической прогрессии и взаимно простыми с разностью этой прогрессии. Действительно, предположив, что есть тройка n, n + k, n + 2k степенных чисел, где НОД(n, k) = 1, можно положить a = k2, b = n·(n + 2k) = n2 + 2kn , причём
НОД(a, b) = НОД(k2 , n2 + 2kn) = НОД(k2 , n(n + 2k)) = 1,
т.к. НОД(n,
k)
= 1 = НОД(k
, n
+ 2k).
Итак, получена a·b·c-тройка
вида: a
= k2,
b
= n·(n
+ 2k)
= n2
+ 2kn,
c
= (n
+ k)2
= n2
+ 2kn
+ k2.
Тогда с учётом того, что r(A2B3)
= r(AB)
![]() ,
получим
,
получим
![]() ,
,
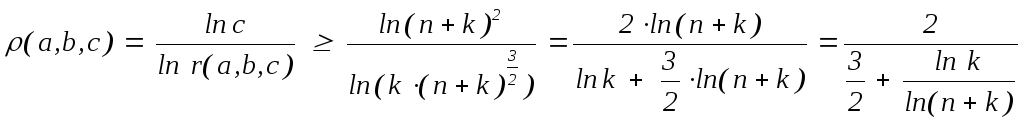 .
.
При фиксированном
k
и стремлении
n
к бесконечности, отношение ![]() стремится к 0.
И тогда при больших n
получим
хитовые abc-тройки
с мерой хитовости
стремится к 0.
И тогда при больших n
получим
хитовые abc-тройки
с мерой хитовости
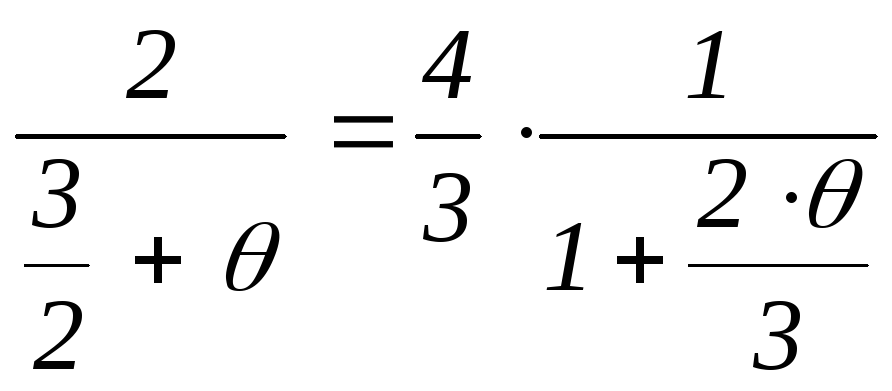 > 1
при любом сколь угодно малом
> 0 . Таких
троек по abc-гипотезе
лишь конечное число.
> 1
при любом сколь угодно малом
> 0 . Таких
троек по abc-гипотезе
лишь конечное число.
10.
Свободные
от квадратов значения многочленов.
До сих пор не было известно ни одного
неразложимого многочлена f(x)
степени не
меньше 5 с
целыми коэффициентами, у которого
значения f(n)
(n
N)
свободны
от квадратов (т.е. являются произведениями
различных простых чисел) для бесконечно
многих n.
Бровкин
Д.,
Филасета
М.,
Гривс
Г.
и
Скинзель
А.
(Browkin J., Filaseta M., Greaves G., Schinzel A.) доказали,
что abc-гипотеза
позволяет утверждать, что этим свойством
обладают многочлены деления круга
Фn(x)
=
![]() и f(x)
=
и f(x)
=
![]() =xn–1
+ xn–2
+ … +
x + 1 (см.
Browkin J., Filaseta M., Greaves G., Schinzel A. Squarefree values
of polynomials and the abc-conjecture // Greaves, G. R. H. (ed.) et
al., Sieve methods, exponential sums, and their applications in
number theory. Proceedings of a symposium, Cardiff, UK, July 17-21,
1995. Cambridge: Cambridge University Press. Lond. Math. Soc. Lect.
Note Ser. 237, 65-85 (1997)).
=xn–1
+ xn–2
+ … +
x + 1 (см.
Browkin J., Filaseta M., Greaves G., Schinzel A. Squarefree values
of polynomials and the abc-conjecture // Greaves, G. R. H. (ed.) et
al., Sieve methods, exponential sums, and their applications in
number theory. Proceedings of a symposium, Cardiff, UK, July 17-21,
1995. Cambridge: Cambridge University Press. Lond. Math. Soc. Lect.
Note Ser. 237, 65-85 (1997)).
11. Гипотеза Чинзеля-Тиджемана (Schinzel-Tijdeman). Эта гипотеза утверждает, что если многочлен p(x) с рациональными коэффициентами имеет по крайней мере 3 простых корня, то диофантово уравнение p(x) = y2z3 имеет лишь конечное число нетривоальных решений (x; y; z). В 1999 г. П. Уолш (Walsh) доказал, что это следует из abc-гипотезы (Walsh P.G. On a conjecture of Schinzel and Tijdeman // Gyoery, Kalman (ed.) et al., Number theory in progress. Proceedings of the international conference organized by the Stefan Banach International Mathematical Center in honor of the 60th birthday of Andrzej Schinzel, Zakopane, Poland, June 30-July 9, 1997. Volume 1: Diophantine problems and polynomials. Berlin: de Gruyter. 577-582 (1999)).
12.
Задача
округления. Пусть
x
– положительное
вещественное число. Тогда для правильного
округления числа
![]() вn-битовой
арифметике нужно вычислить 3n
+ 1 старших
битов. В
2004 г.
Э. Крут,
Р. Ли и Х. Джунь доказали, что
использовав abc-гипотезу,
можно ограничиться 2n
старшими
битами (Croot
E.,
Li
R.,
Zhu
H.
The
abc conjecture and correctly rounded reciprocal square roots //
Theor. Comput. Sci. 315, No. 2-3, 405-417 (2004)).
вn-битовой
арифметике нужно вычислить 3n
+ 1 старших
битов. В
2004 г.
Э. Крут,
Р. Ли и Х. Джунь доказали, что
использовав abc-гипотезу,
можно ограничиться 2n
старшими
битами (Croot
E.,
Li
R.,
Zhu
H.
The
abc conjecture and correctly rounded reciprocal square roots //
Theor. Comput. Sci. 315, No. 2-3, 405-417 (2004)).
