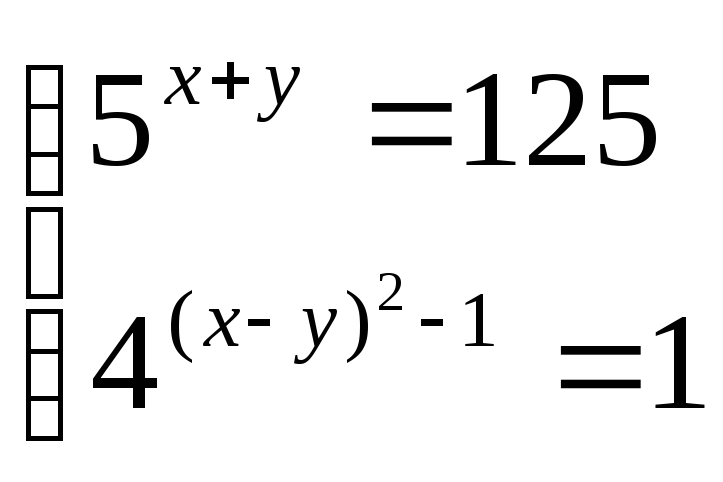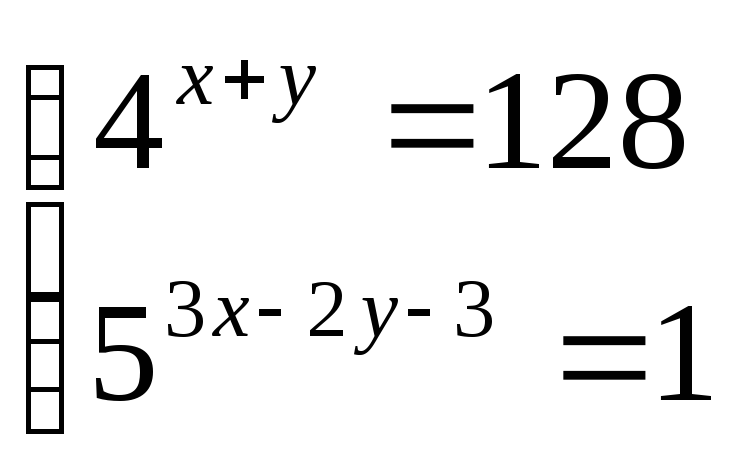- •3) Однородное дифференциальное уравнение I порядка
- •3) Линейное дифференциальное уравнение I порядка (ур-ия Бернулли)
- •Геометрический смысл производной и дифференциала
- •2) Образовательные цели урока
- •3) Приемы создания мотивации учебной деятельности.
- •4) Тестовые задания для текущего контроля усвоения понятия и способы проверки результатов контроля.
- •2) Выберите правильный ответ:
- •3) Решите задачу
- •5) Фрагмент урока на этапе усвоения понятия
- •Свойства счётных множеств:
- •Основные свойства неопределённого интеграла
- •Свойства определённого интеграла
- •1) Вычисление площади плоских фигур.
- •2) Вычисление объёмов тел вращения.
- •3) Вычисление дуги кривой линии.
- •II. Аксиомы умножения:
- •III. Аксиомы дистрибутивности
- •Простейшие свойства групп, колец, полей
- •Гомоморфизмы групп, колец, полей
- •Свойства гомоморфизмов
- •60. Если : u V и : V w – два гомоморфизма групп или колец, то их композиция ○ : u w будет гомоморфизмом групп или колец.
- •70. Если : V w – изоморфизм групп или колец, то обратное отображение –1 : w V также является изоморфизмом групп или колец. Понятие и идея изоморфизма в современной математике
- •Внеклассное мероприятие по математике в 8 классе: «Эта забавная математика»
- •Теорема о поле комплексных чисел
- •Геометрическая интерпретация действий
- •Определение и простейшие свойства векторных пространств. Примеры
- •Подпространство, критерий подпространства, система образующих, базис и размерность векторного пространства. Примеры
- •1) Любое ненулевое конечномерное векторное пространство обладает базисом,
- •2) Любые два базиса конечномерного векторного пространства состоят из одинакового числа векторов.
- •Изоморфизм векторных пространств
- •Примерный план ответа
- •Кольцо матриц Mm n(f) и векторное пространство матриц Mm n(f)
- •Матричные уравнения
- •1.Решите систему уравнений:
- •Билет № 15. Билет №15. Многочлены от одной переменной. Делимость многочлена на двучлен Кольцо f[X] многочленов над полем
- •Деление с остатком в кольце f[X]
- •Рациональные корни многочлена с целыми коэффициентами
- •Освобождение от алгебраической иррациональности в знаменателе дроби
- •Отношение делимости в кольце z и его свойства
- •I. Организационный момент.
- •II. Устный счет.
- •III. Сообщение темы урока
- •IV. Изучение нового материала
- •V. Физкультминутка
- •Алгоритм Евклида
- •Нок целых чисел и его вычисление
- •Вычисление нод и нок целых чисел с помощью канонического разложения
- •Простые и составные числа
- •20. Если произведение нескольких сомножителей делится на p, то, по крайней мере, один из сомножителей делится на p.
- •30. Различные простые числа взаимно просты.
- •50. Если натуральное число n не делится ни на одно простое число p , тоn – простое, в противном случае оно будет составным.
- •II. Урок изучения нового материала.
- •Теоремы Эйлера и Ферма
- •Признаки делимости
- •Учебные задачи для текущего контроля
- •28.Векторное построение геометрии
- •1 Уровень.
- •2 Уровень.
- •3 Уровень.
Билет № 1.V+
Билет № 2.V+
Билет № 3.V-
Билет № 4.V+
Билет № 5.V+
Билет № 6.V+
Билет № 7.V+
Билет № 8.
Билет № 9.
Билет № 10.
Билет № 11.
Билет № 12.
Билет № 13.
Билет № 14.
Билет № 15.
Билет № 16.
Билет № 17.
Билет № 18.
Билет № 19.
Билет № 20.
Билет № 21.V
Билет № 22.V
Билет № 23.V
Билет № 24.применение!
Билет № 25.докозательство
Билет № 26.Допечатать обратную теорему
Билет № 27.V
Билет № 28.V?
Билет № 29.V?
Билет № 30.определение
Билет № 1. «Последовательности».
Последовательность– функция
натурального аргумента (f(n))
гдеn![]() N.
(f(n))=
х1,х2,…,хn,…
N.
(f(n))=
х1,х2,…,хn,…
Если каждому натуральному числу nпоставлено в соответствие одно определенное значение хn, то говорят, что заданапоследовательностьс общим членом хn, пишут (хn).
Послед-ть (хn) наз.возрастающей, если большему номеру соответствует больший член послед-ти, т.еxn+1>xn. Пр: (n)=1,2,3,…,n,…; (n2)=1,4,9,…,n2,…
Послед-ть (хn) наз.убывающей, если большему номеру соответствует меньший член послед-ти, т.е.xn+1<xn. Пр: (1/n)=1,1/2,1/3,…,1/n,…
Послед-ть (хn) наз. стационарной, если все ее члены одинаковые. Пр: (5)=5,5,5,…,5,…
(хn) наз. колеблющейся, если ее члены колеблются около какого-нибудь числа. пр: 1,-1,2,-2,…,n,-n,…
Числовая послед-ть (хn)
наз.ограниченной, если найдётся
такое положительное число с, что для
всехn-членов послед-ти
выполняется неравенство: /xn/![]() c.
c.
Числовая послед-ть (хn)
наз.ограниченной сверху, если
найдётся такое число М, что для всех
членов послед-ти выполняется неравенство:xn![]() М.
М.
Пр: (-n)=-1,-2,…,-n,…sup![]() =-1
=-1
Числовая послед-ть (хn) наз.ограниченной снизу, если найдётся такое числоm, что для всех членов послед-ти выполняется неравенство:xn≥m.
Пр: (n)=1,2,3,…,n,…inf![]() =1
=1
Числовая послед-ть (хn)
наз.ограниченной, если сущ-ютm,M, что для
всех членов послед-ти :m![]() xn
xn![]() М.
М.
Пр: (1/n)=1,1/2,…,1/n,… sup![]() =1
inf
=1
inf![]() =0
=0
Число а наз. пределом числовой
послед-ти с общим членом хn,
если для любого положительного, наперёд
заданного и сколь угодно малого числа![]() ,
найдется такое натуральное числоn0,
что для всех членов послед-ти с номерамиn>n0выполняется неравенство:
,
найдется такое натуральное числоn0,
что для всех членов послед-ти с номерамиn>n0выполняется неравенство:![]() ,
т.е.
,
т.е.![]()
Г![]() еометрический
смысл числовой послед-ти:
еометрический
смысл числовой послед-ти:
![]()
![]()
![]()
![]()
![]()
Геометрический смыслзакл-ся в
том, что внутри окрестности (а -![]() ;а +
;а +
![]() )
находится бесконечное число членов
этой последовательности, а за ее пределами
– конечное (х1,х2,…,хn)
)
находится бесконечное число членов
этой последовательности, а за ее пределами
– конечное (х1,х2,…,хn)
Если число а явл-ся пределом числовой послед-ти, то говорят, что послед-ть сходится к а, а если предела не существует то посл-ть наз-сярасходящейся.
Пр: Доказать, что
![]()
Выберем произвольную
![]() и составим модуль разности
и составим модуль разности![]()
![]() Мы нашлиn0=
Мы нашлиn0=![]() (целое), т.е
(целое), т.е![]() будет выполняться данное неравенство.
будет выполняться данное неравенство.
Послед-ть (αn) наз.бесконечно малой, если![]() .
Послед-ть (хn) наз.бесконечно большой, если
.
Послед-ть (хn) наз.бесконечно большой, если![]() .
.
Т(о единственности предела числ. посл-ти):Если посл-ть (хn) имеет предел, то он единственный.
Док-во:(от противного) предположим,
что посл-ть (хn) имеет
два разных предела![]() и
и![]() ,a≠b,
b>a. Т.к.
,a≠b,
b>a. Т.к. ![]() ,
то по опр.
,
то по опр.![]() ε>0
ε>0![]() n1,
n1,![]() n>n1:
|xn-a|<ε
(1). Т.к.
n>n1:
|xn-a|<ε
(1). Т.к.![]() ,
то для выбр. ε>0
,
то для выбр. ε>0![]() n2,
n2,![]() n>n2:
|xn-b|<ε
(2). Обозначим черезn0=max{n1;n2},
тогда для люб.n>n0:
(1),(2). Составим разностьb-a=|b-a|=|b-a+хn-хn
|=|(хn–a)-(хn–b)|
≤| хn-a|+|
хn-b|<ε+ε=2ε
(|x
n>n2:
|xn-b|<ε
(2). Обозначим черезn0=max{n1;n2},
тогда для люб.n>n0:
(1),(2). Составим разностьb-a=|b-a|=|b-a+хn-хn
|=|(хn–a)-(хn–b)|
≤| хn-a|+|
хn-b|<ε+ε=2ε
(|x![]() y|≤|x|
y|≤|x|![]() |y|)
|y|)
Т.о. b-a<2ε.
Т.к.ε-произвольное, пусть
![]() =
=![]() ,
,![]() b-a<2*
b-a<2*![]() ,b-a
не< b-a
,b-a
не< b-a
![]() получили
противоречие, оно говорит о том, что
наше предположение неверно. Т.о.,
получили
противоречие, оно говорит о том, что
наше предположение неверно. Т.о.,![]() -
единственный
-
единственный
Т:Если![]() и
и![]() ,
то
,
то
1)
![]() ; 2)
; 2)![]()
3)
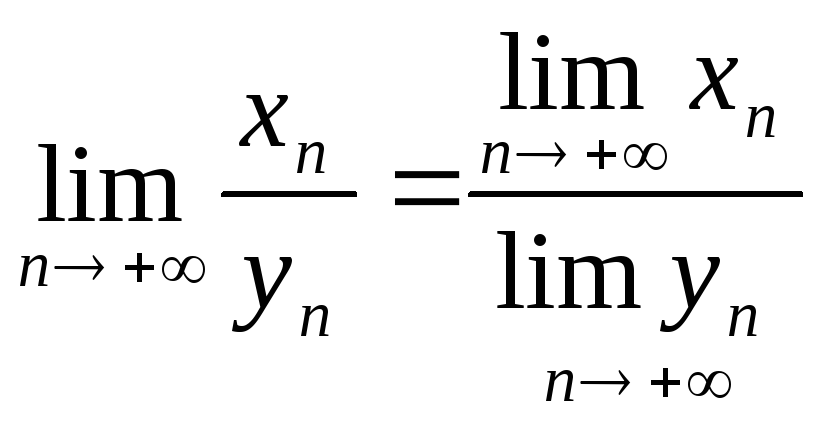 ,
если
,
если![]() ;
;
4)
![]() ,
гдеC=const;
5)
,
гдеC=const;
5)![]() .
.
МЕТОДИКА 1.
Урок алгебры по теме "Арифметическая прогрессия" для 9 класса
Цели
Обучающие: - формировать понятие арифметической прогрессии, ознакомить учащихся с формулой нахождения n-го члена арифметической прогрессии;
- формировать навыки нахождения n-ого члена арифметической прогрессии; сформировать навыки использования формулы n-ого члена арифметической прогрессии при решении задач;
Развивающие: развивать умение делать выводы, обобщать и конкретизировать, логическое мышление, память; развивать навыки самоконтроля, самообразования; развивать умения: работать индивидуально, работать на результат.
Воспитательные:воспитать трудолюбие, усидчивость, самостоятельность, последовательность и аккуратность ведения записей, повысить интерес к изучаемому материалу.
Тип урока: Изложение нового материала
Структура урока:
Сообщение темы, цели урока, мотивация учебной деятельности (орг.момент);
Подготовительный этап через повторение и актуализацию опорных знаний;
Ознакомление с новым материалом;
Первичное осмысление;
Постановка задания на дом;
Итог.
Для создания положительной мотивации можно использовать историческую задачу. Ее не обязательно решать до конца, достаточно только с ее помощью ввести определение последовательности. А на этапе первичного закрепления вернуться к задаче и дорешать ее.
Историческая задача.
Задачи на прогрессии, дошедшие до нас из древности, были связаны с запросами хозяйственной жизни: распределение продуктов, деление наследства и др. Вот одна из них:
«Сто мер хлеба разделили между 5 людьми так, чтобы второй получил на столько же больше первого, на сколько третий получил больше второго, четвертый больше третьего и пятый больше четвертого. Кроме того, двое первых получили в 7 раз меньше трех остальных. Сколько нужно дать каждому?»
Решение. Обозначим долю первого за x, разница -y. Тогда:
Доля первого - x,
Доля второго - x+y,
Доля третьего - x+2y,
Доля четвертого - x+3y,
Доля пятого - x+4y.
Мы получили последовательность, которая называется арифметической пргрессией.
Рассмотрим определение арифметической прогрессии.
Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом.
То есть, последовательность (an) – арифметическая прогрессия, если для любого натурального выполняется условиеan +1 = an+d, гдеd- некоторое число.
Из определения арифметической прогрессии следует, что разность между любым ее членом, начиная со второго, и предыдущим членом равна, т.е. при любом натуральном верно равенство a n+1 – an= d.
Число dназываетсяразностью арифметической прогрессии.
Чтобы задать арифметическую прогрессию, достаточно узнать ее первый член и разность. Например:
1. Еслиa1=1 иd=1, то получим арифметическую прогрессию
1; 2; 3; 4; 5;…, члены которой – последовательные натуральным числа.
2. Еслиa1=1 иd=2, то получим арифметическую прогрессию
1; 3; 5; 7; 9;…, которая является последовательностью положительных нечетных чисел.
3. Еслиa1=-2 иd=-2, то получим арифметическую прогрессию
-2; -4; -6; -8; -10;…, которая является последовательностью отрицательных четных чисел.
4. Еслиa1=7 иd=0, то имеем арифметическую прогрессию
7; 7; 7; 7; 7;…, все члены которой равны между собой.
Зная первый член и разность арифметической прогрессии, можно найти любой ее член, вычисляя последовательно второй, третий, четвертый и т.д. члены. Однако для нахождения члена прогрессии с большим номером такой способ неудобен. Постараемся отыскать способ, требующий меньшей вычислительной работы.
Зная, определение арифметической прогрессии можно вывести формулу n-го члена прогрессии
Исходя из определения арифметической прогрессии:
a2=a1+d,
a3=a2+d=(a1+d)+d=a1+2d,
a4=a3+d=(a1+2d)+d=a1+3d,
a5=a4+d=(a1+3d)+d=a1+4d.
Точно так же находим, что a6= a1+5d, и вообще, чтобы найтиan, нужно кa1 прибавить(n-1)d, т.е.
an=a1+(n-1)d.
Получили формулы n-го члена арифметической прогрессии.
Формулу n-го члена арифметической прогрессииan=a1+(n-1)d можно записать иначе:
an=dn+(a1-d).
Отсюда ясно, что любая арифметическая прогрессия может быть задана формулой вида an=kn+b,
где k и b - некоторые числа.
Верно и обратное: последовательность (an), заданная формулой вида an=kn+b,
где k и b - некоторые числа, является арифметической прогрессией.
Закрепление материала
Изучив новый материал его необходимо закрепить
Задача 1. Проверить, какие из следующих конечных последовательностей являются арифметическими прогрессиями, и найти иха1иd. а) 1, 4, 7, 10; б) 1, 4, 15, 18; в) 1, -2, -5, -6; г) 1, -1, -3, -5.
Ответ:а, г.
Задача 2. В арифметической прогрессии (an), известно, чтоa1=2 иa11=-11. Найти разность арифметической прогрессииd.
Ответ: d=-1,3.
Задача 3. Выписать первые пять членов арифметической прогрессии, у которойа1=3,d=2.
Ответ: 3, 5, 7, 9, 11.
Задача 4. Является ли число 22,5 членом арифметической прогрессии (an): 6,8; 8; ..?
Ответ: число 22,5 не является членом данной арифметической прогрессии.
Задача 5. Курс воздушных ванн начинают с 15 мин. в первый день и увеличивают время этой процедуры в каждый следующий день на 10 минут. Сколько дней следует принимать ванны в указанном режиме, чтобы достичь их максимальной продолжительности 1 час 45 минут?
Ответ: 10 дней следует принимать ванны
Билет № 2. «Функция».
П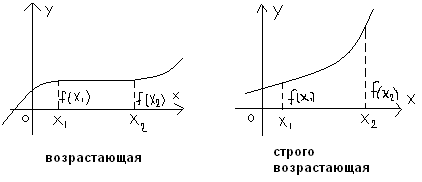 усть
даны два числовых мн-ваXи У, и задано некоторое отобр-иеf.
Если каждому элементу
усть
даны два числовых мн-ваXи У, и задано некоторое отобр-иеf.
Если каждому элементу![]() соответствует
единственное значение
соответствует
единственное значение![]() и
при этом каждому значению у поставлено
в соответствие единственное зн-ие х, то
говорят, что между мн-вами Х и У установлено
ВОС, кот-ое и наз-сяфункцией.
и
при этом каждому значению у поставлено
в соответствие единственное зн-ие х, то
говорят, что между мн-вами Х и У установлено
ВОС, кот-ое и наз-сяфункцией.
Х– область опр-ия ф-ции.
у=f(x) возраст., если большему значению аргумента соотв-ет большее зн-ие ф-ции
у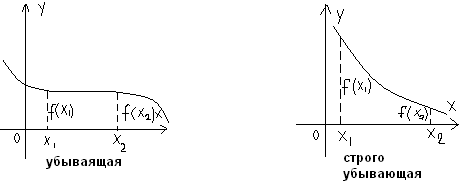 =f(x)
убыв., если большему значению
аргумента соотв-ет меньшее значение
ф-ции
=f(x)
убыв., если большему значению
аргумента соотв-ет меньшее значение
ф-ции
у=f(x)-периодическая с периодом Т, еслиf(x+Т)=f(x)
у=f(x)-четнаяна симметричном отн-но т.0 (начала координат) промежутке, еслиf(-x)=f(x).
у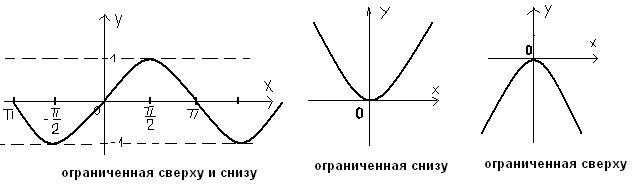 =f(x)-нечетнаяна симметричном отн-но т.0 (начала
координат) промежутке, еслиf(-x)=-f(x).
=f(x)-нечетнаяна симметричном отн-но т.0 (начала
координат) промежутке, еслиf(-x)=-f(x).
у=f(x)-ограничена
сверху, если
![]() М,
М,![]() х
х![]() Х:f(x)≤M
Х:f(x)≤M
у=f(x)-ограничена
снизу, если
![]() m,
m,
![]() х
х![]() Х:f(x)≥m
Х:f(x)≥m
у=f(x)-ограниченная,
если
![]() К>0,
К>0,![]() x
x![]() Х:|f(x)|≤К
Х:|f(x)|≤К
у=f(x)-явная
у=F(x,y)-неявная
Число а наз. пределом ф-цииf(x)
в точке х0, если![]() ε>0,
найдётся δ>0 зависящее от ε, то для
ε>0,
найдётся δ>0 зависящее от ε, то для![]() удовлетворяющих неравенству
удовлетворяющих неравенству![]() :
:![]() ,
т.е.
,
т.е.![]()
Г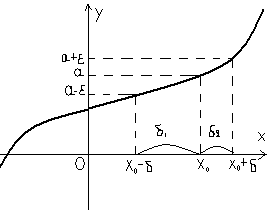 еометрический
смысл:
еометрический
смысл:![]()
![]()
![]()
![]() ,
т.е.
,
т.е.![]()
Когда х попадает в δ-окрестность точки
х0, х![]() соответствующее значение ф-ции попадает
в ε-окрестность точки а
соответствующее значение ф-ции попадает
в ε-окрестность точки а![]()
Т: Пусть![]() и
и![]() ,
то
,
то
1)
![]() ,
2)
,
2)![]()
3)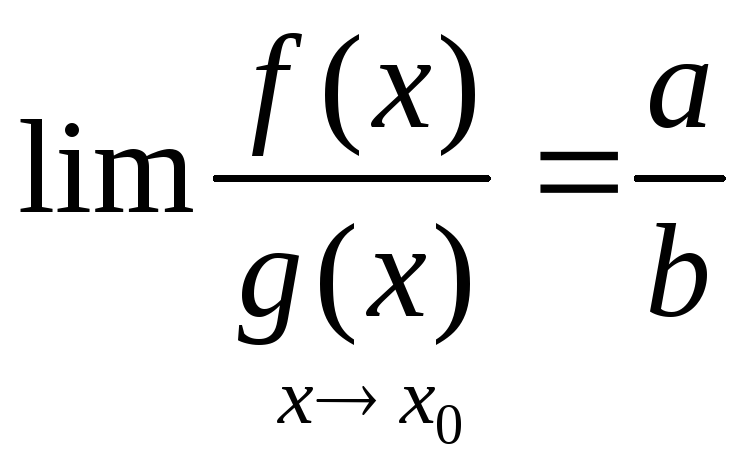 ,
,![]() ,4)
,4)![]() ,5)
,5)![]()
Док-во:1) На основании теоремы,
что если ф-ция имеет своим пределом
число а, то она может быть представлена
в виде суммы своего предела и бесконечно
малойf(x)=a+
α(х) при х→х0, т.е.f(x)=a+α(х), где α(x)-бесконечно
малая при х→х0, аg(x)=a+β(х),
где β(х)-бесконечно малая при х→х0![]() f(x)+g(x)=(a+b)+
(α(х)+β(х)), то по обратной теореме: если
ф-ция м/б представлена в виде суммы числа
и бесконечно малого, то это число явл-ся
пределом для данной ф-ции.
f(x)+g(x)=(a+b)+
(α(х)+β(х)), то по обратной теореме: если
ф-ция м/б представлена в виде суммы числа
и бесконечно малого, то это число явл-ся
пределом для данной ф-ции.
2) Тоже самое, только : f(x)*g(x)=(a*b)+ (b*α(х) +a*β(х) + α(х)*β(х)), то по обр. теореме доказано.
3)![]() α(x),β(х)-бесконечно
малые, при х→х0.
α(x),β(х)-бесконечно
малые, при х→х0.![]() -бесконечно
малое, при х→х0
-бесконечно
малое, при х→х0
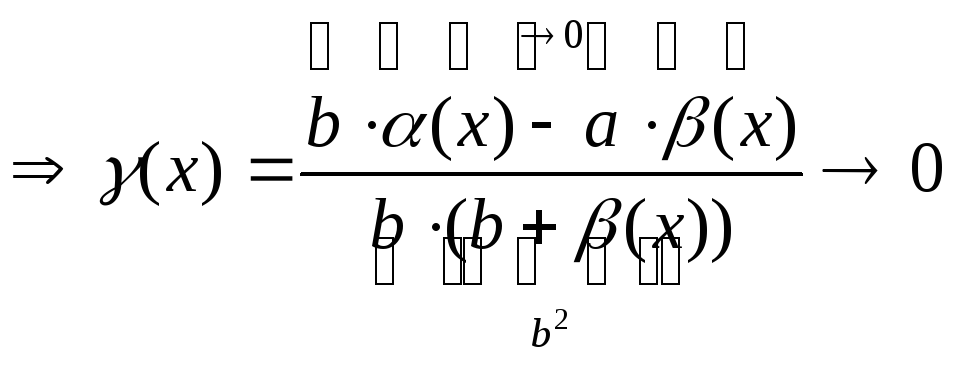
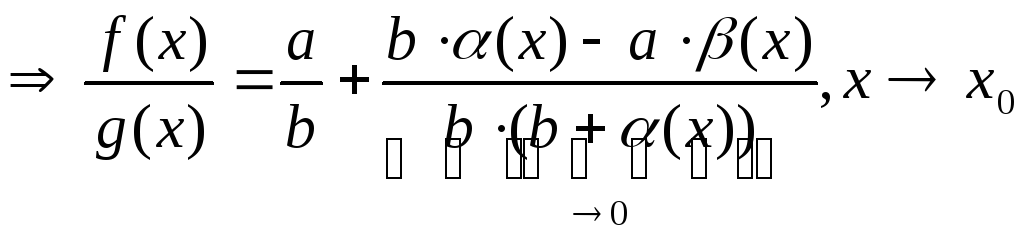 ,
то по обр. теореме доказано.
,
то по обр. теореме доказано.
![]() - 1-ый зам. предел
- 1-ый зам. предел![]() - 2-ой зам. предел
- 2-ой зам. предел
Пусть ф-ция f(x)
определена на мн-ве Х, а (.)х0![]() Х,
то ф-цияf(x)непрерывнав (.)х0:
Х,
то ф-цияf(x)непрерывнав (.)х0:![]()
(по Коши)Ф-цияf(x)непрерывнав (.)х0![]() .
.
(по Гейне) Ф-цияf(x)непрерывнав (.)х0, если какую бы послед-ть различных точек х1,х2,…,хn,… сходящихся к х0не взять, послед-ть соответствующих значений ф-цийf(х1),f(х2),…,f(хn),… сходится кf(х0).
(на яз.приращ)Ф-цияf(x)непрерывнав (.)х0, если бесконечно малому приращению аргумента соответствует бесконечно малое приращению ф-ции.
Точка х0наз.точкой разрываф-цииf(x), если в ней нарушено какое-либо условие непрерывности, а именно:
f
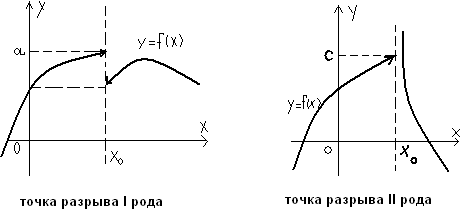 (x)
м/б неопределенна в (.)х0(не
существовать);
(x)
м/б неопределенна в (.)х0(не
существовать);м/б не существует предел ф-ции f(x) при х→х0;
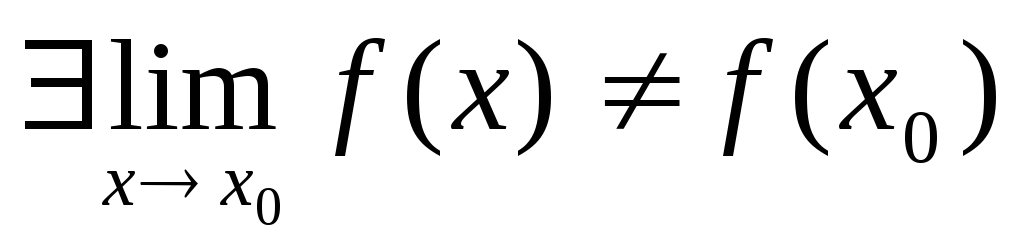
Точка х0наз.точкой устранимого разрыва, если предел в этой точке существует но не равенf(x0)- значению ф-ции или предел в этой точке существует, но сама ф-ция в (.)х0не определена.
Точка х0наз.точкой разрыва I рода, если односторонние пределы существуют, но не равны между собой.
Точка х0наз.точкой разрыва
II рода,
если хотя бы один из односторонних
пределов не существуют или равен![]() .
.
Т(1-ая Т.Больцано-Коши):Если ф-ция у=f(x) непрерывна на отрезке [a,b] и на концах отрезка принимает значения разных знаков, то найдётся хотя бы одна (.)с є [a,b], в которой ф-ция обращается в 0, т.е.f(с)=0.
Т(2-ая Т. Б-К):Если ф-ция у=f(x) непрерывна на отрезке [a,b] и принимает на его концах разные значения, то какое бы число М мы не взяли, лежащее междуf(a) иf(b), то внутри отрезка [a,b] найдётся такая (.)С, в которойf(С)=М.
Док-во:
Пусть f(a)<f(b),f(a)<М<f(b).
Рассм. φ(х)=f(x)-Mи найдем ее значение на концах отрезка:φ(a)=f(a)-M<0; φ(b)=f(b)-M>0; φ(x)-непр. как разность непр. ф-ции и константы (1Т.Б-К). Значит внутри отрезка [a,b] найдется такая т.С, в которой ф-ция
φ(с)=0![]() f(c)-M=0
f(c)-M=0![]() f(c)=M
f(c)=M
Т(1-ая Т.Вейерштрасса):Если ф-ция у=f(x) непрерывна на отрезке [a,b], то она на нем ограничена .
Т(2-ая Т.В): Если ф-ция у=f(x) непрерывна на отрезке [a,b], то она достигает на этом отрезке своих наибольших и наименьших значений.
МЕТОДИКА 2. «Понятие функции и способы задания функции»
Основные понятия темы:независимая и зависимая переменные, функция, область определения, область значений ф-ии, графики ф-ии.
Основные предложения темы:
- свойства функции (область определения, область значения, монотонность, периодичность, четность, нечетность, нули функции, промежутки знакопостоянства, экстремумы, непрерывность).
- способы задания функции (аналитический, табличный, графический, описание).
Фрагмент урока: «Понятие ф-ии» 7 класс
Тип урока: изучения нового материала
Цели:
Обучающие:- изучить основные функциональные понятия;
Развивающие:- развитие операционное мышление: умение анализировать, сравнивать, обобщать;
- развитие мировоззрения, речи, памяти;
Воспитательные:- воспитание интереса к математике;
- эстетическое воспитание.
Содержание урока:
Организационный момент (2-3 мин)
Актуализация знаний (6-7 мин)
Изучение нового материала (13-14 мин)
Усвоение нового материала (17-18 мин)
Домашнее задание (2-3 мин)
Итоги урока (2-3 мин)
Мотивация к изучению темы: «Понятие функции».
В зависимости от возрастных особенностей выделяют следующие методы мотивации: 1. проблемный способ изложения материала, 2. эмоциональный характер, 3. связь с практикой, с жизнью, 4. связь с прошлым материалом, 5. научно-факторная содержательность материала, 6. коллективная работа.
С учетом возрастных особенностей учащихся воспользуемся одним из методов мотивации – связь с жизнью – и подведем их к понятию функция, показав зависимость одной величины от другой, решив следующие задачи.
Задача 1.Из пункта А в пункт В отправился пешеход. Траектория пути изображена на графике. Расстояние от пункта А до пункта В 20 верст. Сколько верст прошел пешеход спустя 2 часа, 4 часа, 8 часов, 18 часов.
(для наглядности используется плакат с изображением графика зависимости)
 Задача 2. На окраине леса шириной
100м запыленность воздуха составляет
65% от запыленности на открытом месте,
на расстоянии 400м от края леса она
снижается до 38%, 1000м – до 25%, 3км – до 5%.
Постройте график зависимости уменьшения
запыленности по мере удаления в лес.
Задача 2. На окраине леса шириной
100м запыленность воздуха составляет
65% от запыленности на открытом месте,
на расстоянии 400м от края леса она
снижается до 38%, 1000м – до 25%, 3км – до 5%.
Постройте график зависимости уменьшения
запыленности по мере удаления в лес.

Рис.1
Таким образом, ребята, зависимость переменной yот переменнойx называетсяфункцией, если каждому значениюxсоответствует единственное значение у
Билет № 3.«Дифференциальныеуравнения».
Уравнение, содержащее независимую
переменную x, функциюу и ее производнуюу',![]() (не разрешимое) наз.дифференциальным
уравнение I
порядка(д/у) и обозначается:
(не разрешимое) наз.дифференциальным
уравнение I
порядка(д/у) и обозначается:![]() .
.
Интегралом диф-го урав-я
наз. соотношение, связывающее
независимые переменные и искомую ф-цию,
т.е.![]() -
интеграл диф-го урав-я
-
интеграл диф-го урав-я![]() -
решение.
-
решение.
Условие
![]() при
при![]() наз.начальным условием. (или
наз.начальным условием. (или![]() ,
или
,
или![]() )
)
Общим решением д/уI порядка наз.
ф-ция![]() ,
где с- произвольная постоянная,
удовлетворяющая двум условиям:
,
где с- произвольная постоянная,
удовлетворяющая двум условиям:
1) она удовлетворяет данному д/у при любом конкретном значении с;
2) каково бы ни было начальное условие
![]() можно
найти такое значение
можно
найти такое значение![]() ,
что ф-ция
,
что ф-ция![]() б/т удовлетворять начальным условиям.
б/т удовлетворять начальным условиям.
Д/у устанавливает связь (зависимость) между координатами точки (х;y) и угловым коэффициентом y'касательной к интегральной кривой, проходящей через эту точку. Следовательно, д/уy'=ƒ(х;y) дает совокупность направлений (семейство кривых) на плоскости Охy. Таково геометрическое истолкование д/уIпорядка
Частным решением д/уI
порядканаз. любая ф-ция![]() ,
которая получается из общего решения
при конкретном значении произвольной
постоянной
,
которая получается из общего решения
при конкретном значении произвольной
постоянной![]() .
.
Т(о существовании и единственности
решения д/у I
порядка):Если в д/у![]() правая часть
правая часть![]() и
частная производная
и
частная производная![]() явл-ся непрерывной вD,
содержащую искомую (.)М(х0,у0)
явл-ся непрерывной вD,
содержащую искомую (.)М(х0,у0)![]() D, то
D, то![]() ,
и при том единственное решение этого
урав-я
,
и при том единственное решение этого
урав-я![]() ,
которое удовлетворяет начальному
условию:
,
которое удовлетворяет начальному
условию:![]() при
при![]() .
.
В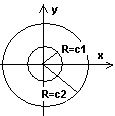 иды
уравнений:
иды
уравнений:
1) Уравнения с разделёнными переменными. Уравнения видаP(x) dx + Q(y) dy = 0.
∫P(x) dx +∫Q(y) dy = c- общий интеграл (общее решение) этого уравнения.
Пр:![]() - уравнение с разделяющимися коэффициентами
- уравнение с разделяющимися коэффициентами
![]()
![]()
![]()
![]()
![]()
![]()
![]() - общий интеграл.
- общий интеграл.
С точки зрения геометрии получим мн-во окружностей.
2) Уравнения с разделяющимися
переменными. Уравнение вида![]()
![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]() общий интеграл.
общий интеграл.
П![]() р:
р:
При такой форме записи общего интеграла
решение y= 1 потеряно. Можно
преобразовать общее решение к виду,
который содержит это решение. Переобозначим
постояннуюCкак ln|C1|:![]() Вернёмся
к обозначению постоянной интегрированияC; общее решение
Вернёмся
к обозначению постоянной интегрированияC; общее решение![]() содержит
частное решениеy= 1 приC= 0.
содержит
частное решениеy= 1 приC= 0.
3) Однородное дифференциальное уравнение I порядка
Ф-ция f(x,y)
наз.однородной ф-циейстепени
однородностиnотносительно
переменныхx,y,
если для![]() справедливо тождество:
справедливо тождество:![]() .
.
Уравнением
![]() наз.однородным д/у, если его правая
часть, ф-цияf(x,y)
явл-ся однородной ф-цией нулевой степени
однородности относительноx,y.
наз.однородным д/у, если его правая
часть, ф-цияf(x,y)
явл-ся однородной ф-цией нулевой степени
однородности относительноx,y.
Уравнение
![]() наз.однородным д/у I
порядка, если ф-цияP(x,y),Q(x,y)
– однородные ф-ции одной и той же степени
однородности.
наз.однородным д/у I
порядка, если ф-цияP(x,y),Q(x,y)
– однородные ф-ции одной и той же степени
однородности.
Произведём дополнительное преобразование
д/у. f(x,y)
явл-ся однородной ф-цией нулевой степени
однородности![]()
![]()
![]() ,
т.к.
,
т.к.![]() -
любое, возьмём
-
любое, возьмём![]() .
.
![]()
![]()
![]()
![]()
Уравнение
![]() наз.однородным д/у I
порядка, если его правая часть м/б
представлена как ф-ция т/о отношения
переменных
наз.однородным д/у I
порядка, если его правая часть м/б
представлена как ф-ция т/о отношения
переменных![]()
![]() м/д решения: подстановка
м/д решения: подстановка![]() ,
,![]() -
новая искомая ф-ция.
-
новая искомая ф-ция.
![]()
![]() - ур-ие с раздел. перем.
- ур-ие с раздел. перем.
![]() /
/![]()
![]()
![]()
![]()
Проинтегрировав, получим общий интеграл содержащий x,t и возвращаемся к прежним переменным.
Пр: 1)
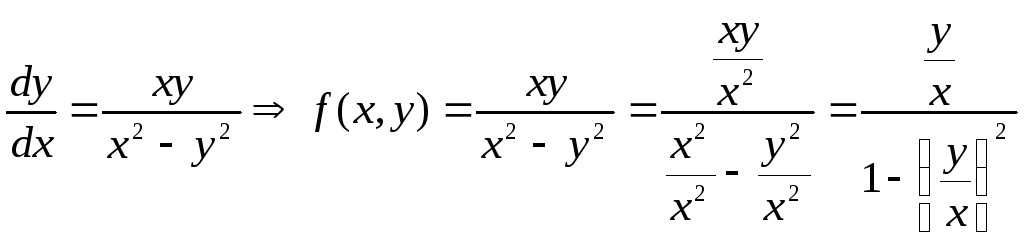 ;
;
Замена:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
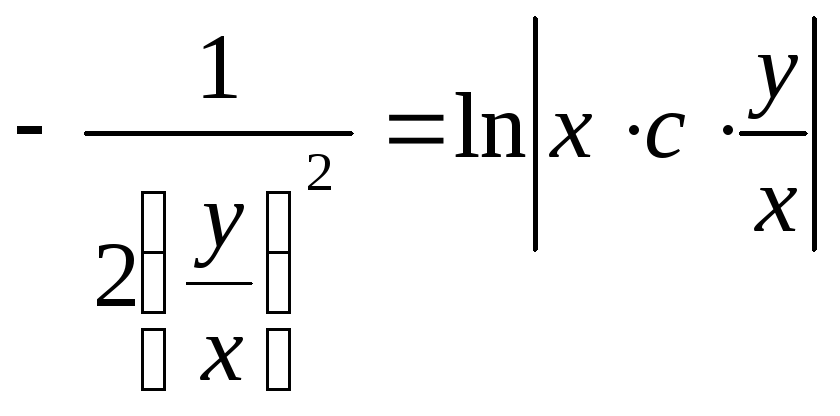
![]()
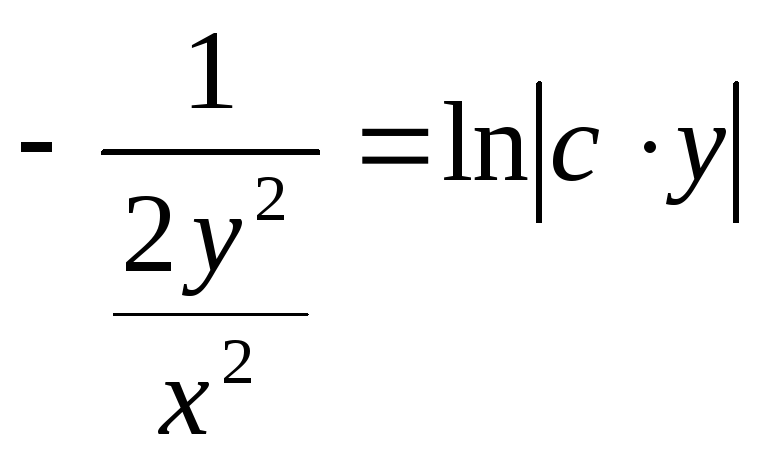
![]()
![]()
3) Линейное дифференциальное уравнение I порядка (ур-ия Бернулли)
Линейное д/у I
порядканаз. уравнение![]() ,
где
,
где![]() -
данные известные ф-ции. Искомая ф-ция у
и её производная
-
данные известные ф-ции. Искомая ф-ция у
и её производная![]() не
должны умножаться друг на друга и
делится.
не
должны умножаться друг на друга и
делится.
Линейное дифференциальное уравнение интегрируется несколькими способами: метод Бернулли и метод вариации произвольной постоянной.
Общее решение данного урав-я ищется в
виде произведения двух ф-ций
![]() ,
пока неизвестных:
,
пока неизвестных:![]() или
или![]()
![]() .
Подставим значения для у и
.
Подставим значения для у и![]() в данное уравнение:
в данное уравнение:![]()
![]()
![]()
Пр:
![]() Приведём данное уравнение к стандартному
виду, т.е. разделим на х:
Приведём данное уравнение к стандартному
виду, т.е. разделим на х:
![]()
![]()
![]() - линейное д/уIпорядка.
Ищем общее решение:
- линейное д/уIпорядка.
Ищем общее решение:![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() /
/![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() /
/![]()
![]()
![]()
![]()
![]()
Ответ:
![]()
3. Тема: «Простейшие дифференциальные уравнения».Тип урока: изучение нового материала (урок-практикум).Класс: 11 класс (математического профиля). Учебник: Ш.А.Алимов, Ю.М.Колягин, Ю.В.Сидоров. Алгебра и начала анализа.Обучающие:формировать умение решать задачи на дифференцирование и интегрирование;выделить разные виды решения задач, расширить кругозор учащихся.Воспитательные: воспитание внимательности, аккуратности, трудолюбия;воспитание интереса к предмету.Развивающие:развивать коммуникативные способности;развивать креативность мышления; расширить кругозор учащихся.Структура урока:Организационный момент;Сообщение темы урока, постановка целей урока;Объяснение нового материала;Закрепление нового материала (решение практических задач);Подведение итогов урока;Домашнее задание.Психологическая характеристика юношеского возрастаСтабилизация многих физиологических функций, формирование телесной конституции, свойственной взрослому человеку, позволяет юношам и девушкам учувствовать в различных видах производственного труда. Трудовая деятельность способствует обогащению теоретических знаний, полученных во время учебы, расширению кругозора, а главное – формированию качеств необходимых для будущей профессиональной деятельности, для самореализации. Необходимость выбора дальнейшего жизненного пути, избрание той или иной профессии является наиболее важной особенностью этого возраста.Черты личности в юношеском возрасте определяются теми психологическими новообразованиями, которые зарождаются еще в подростковом возрасте: усиление интереса к своей собственной личности, стремление к самостоятельности взрослости; проявление критичности и т.д., но они несколько видоизменятся. У человека основным содержанием деятельности является труд, создание материальных и духовных ценностей. Отношение индивида к виду опосредуется теперь его отношением к обществу и культуре. Отсюда – качественно иное, чем у животных, содержание понятий созревание и подготовка к жизни. Созревание предполагает, таким образом, социализацию, и не может осуществляться вне её и помимо её. Поэтому и переходный возраст это этап развития личности, процесс перехода от зависимого, опекаемого детства, когда ребенок живет по правилам взрослых, к самостоятельной и ответственной деятельности взрослого человека.В психолого-педагогической литературе акцент делается не на физическом развитии, а на смене ведущих форм деятельности. Божович Л.И. определяет старший школьный возраст как юношеский, сосредоточив свое внимание на: развитии мотивационной сферы личности; определение старшеклассников своего места в жизни и внутренней позиции; формировании мировоззрения и его влияния на познавательную деятельность; самосознания и морального сознания.Методический материал:ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ. Многие физические законы, которым подчиняются те или иные явления, записываются в виде математического уравнения, выражающего определенную зависимость между какими-то величинами. Часто речь идет о соотношении между величинами, изменяющимися с течением времени, например экономичность двигателя, измеряемая расстоянием, которое автомашина может проехать на одном литре горючего, зависит от скорости движения автомашины. Соответствующее уравнение содержит одну или несколько функций и их производных и называется дифференциальным уравнением. (Темп изменения расстояния со временем определяется скоростью; следовательно, скорость – производная от расстояния; аналогично, ускорение – производная от скорости, так как ускорение задает темп изменения скорости со временем.) Большое значение, которое имеют дифференциальные уравнения для математики и особенно для ее приложений, объясняются тем, что к решению таких уравнений сводится исследование многих физических и технических задач. Дифференциальные уравнения играют существенную роль и в других науках, таких, как биология, экономика и электротехника; в действительности, они возникают везде, где есть необходимость количественного (числового) описания явлений (коль скоро окружающий мир изменяется во времени, а условия изменяются от одного места к другому).
Дифференциальные уравнения являются одним из самых мощных средств математического решения практических задач. Особенно широко они используются для решения задач естественнонаучного цикла: механики, физики, химии и биологии. Во многих задачах геометрической оптики, геодезии, картографии и других областей естествознания возникает необходимость нахождения кривых по заданным свойствам проведенных к ним касательным. Обычно такие геометрические задачи решаются так же с помощью дифференциальных уравнений.
Билет № 4. Показательная функция.
Показательной функцией называется функция у = ах, где а – заданное число, а > 0, а ≠ 1;
Решение показательных уравнений часто сводится к решению уравнения ах= аb, где а > 0, а ≠ 1, х – неизвестное.
Основные свойства степени. Пусть a > 0, b > 0, x, x1и x2– любые действительные числа. Тогда
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Свойства показательной функции:
Область определения показательной функции – множество Rвсех действительных чисел.
Это свойство следует из того, что степень
![]() ,
где
,
где![]() ,
определена для всех
,
определена для всех![]() .
.
Множество значений показательной функции – множество всех положительных чисел.
Чтобы убедиться в этом, нужно показать,
что уравнение ![]() ,
где
,
где![]() а ≠ 1, не имеет корней при любом
а ≠ 1, не имеет корней при любом![]() .
По свойству степени
.
По свойству степени![]() это
уравнение не имеет корней, если
это
уравнение не имеет корней, если![]() .
То, что это уравнение имеет корень при
любом
.
То, что это уравнение имеет корень при
любом![]() Это означает, что любая прямая
Это означает, что любая прямая![]() ,
где
,
где![]() ,
пересекается с графиком показательной
функции.
,
пересекается с графиком показательной
функции.
Показательная функция y = axявляется возрастающей на множестве всех действительных чисел, если a > 1, и убывающей, если 0 < a < 1.
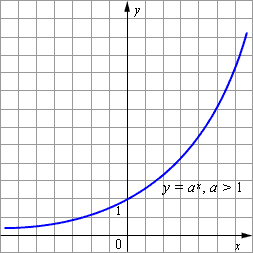
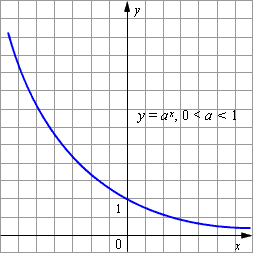
Разложение в степенной ряд показательной функции
![]()
![]()
![]()
![]()
![]()
![]()
МЕТОДИКА 4. Формы, виды и средства контроля знаний и умений.
Формы контроля знаний и уменийучащихся выделяются в соответствии с формами обучения:
массовая (групповая, фронтальная);
индивидуальная: фронтальный и индивидуальный опрос, контрольная работа, зачет, экзамен, диктант, сочинение.
Виды контроля:
По конечному результату:
пошаговый контроль (за операциями);
контроль, связанный с установлением определенных параметров деятельности.
По месту в процессе обучения:
текущий (в ходе учения):
предварительный;
ежедневный;
периодический;
итоговый по теме;
итоговый по курсу обучения.
В новых педагогических технологиях рассматриваются следующие виды контроля усвоения знания и способов деятельности:
входной;
текущий, или промежуточный;
итоговый.
Средства контроля:математический диктант, дидактические материалы, карточки, тесты, перфокарты, таблицы, опорные схемы, задания с печатной основой; кодоскоп, модели и приборы и т.д.
Задания для организации контроля на основе технологического подхода.
Входной контроль
Вариант №1
Инструкция: подчеркните ответ «да», если вы согласны с данным утверждением; если не согласны – «нет».
Текст задания.
Показательное уравнение имеет вид: ах= b. (да, нет)
Область значения функции y = ax– множество натуральных чисел. (да, нет)
При любых действительных значениях x и y справедливо равенство: (ax)y= ax+y (да, нет)
Функция y = axвозрастает при a > 1 и убывает при 0 < a < 1. (да, нет)
Уравнение ах= b не имеет решений в случае b > 0 или b ≠ 0. (да, нет)
Эталон ответа: да, нет, нет, да, нет.
Вариант №2
Инструкция:заполните пропуски так, чтобы получилось верное утверждение.
Текст задания.
Функция, заданная формулой y = ax(где a > 0, a ≠ 1), называется показательной функцией с _________________ а.
Область определения показательной функции – множество ___________________ чисел.
Уравнение ах= b при любом положительном a, отличном от 1, и b > 0 имеет _______________________корень.
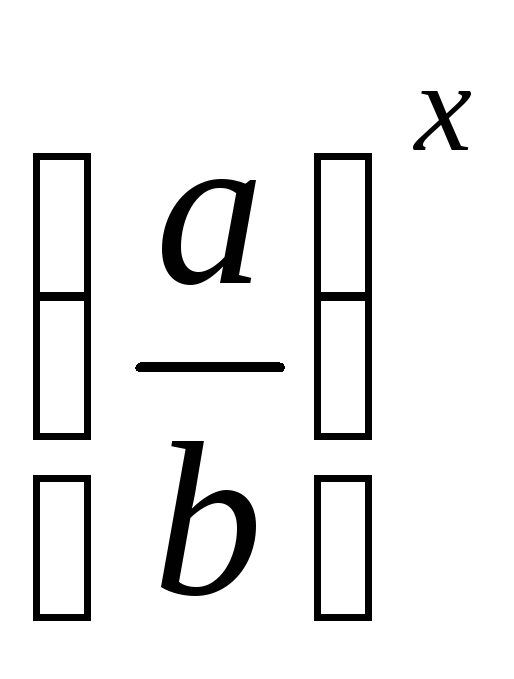 =
…
=
…Показательная функция пересекает ось OY в точке с координатами _____.
Эталон ответа: 1 - основанием а; 2 –
действительных; 3 – единственный; 4 -
![]() ;
5 - (0; 1).
;
5 - (0; 1).
Текущий контрольпо теме «Показательные уравнения»
Решите уравнения:
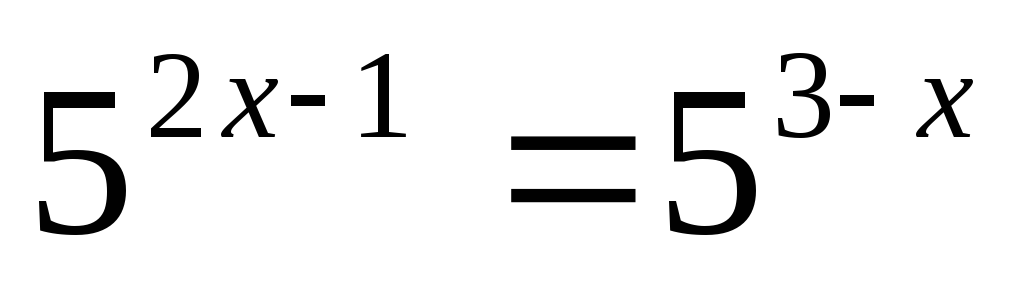
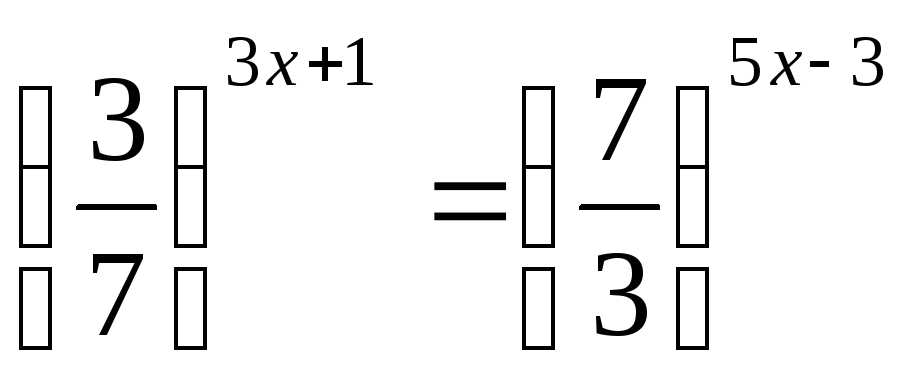
9х– 43х+ 3 = 0;
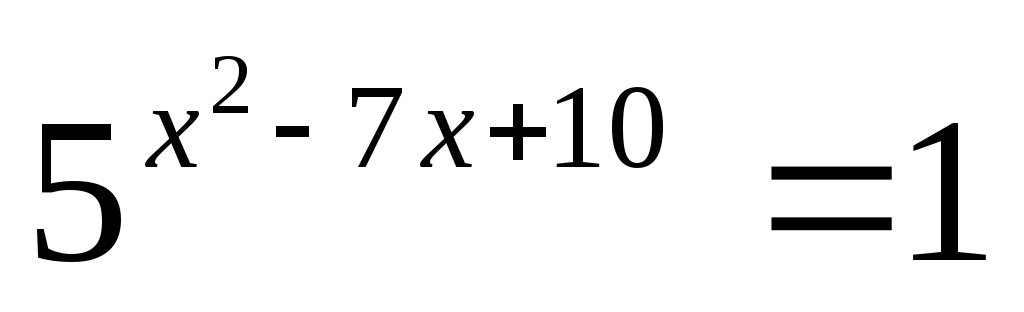
Итоговый контрольиспользован для проведения контрольной работы. (см. фрагмент урока)
Фрагмент урока на этапе контроля.
Тема: «Показательная функция».
Цели урока: Обучающая – выявить уровень овладения учащимися комплексом знаний и умений по теме «Показательная функция»;
Развивающая – развитие памяти, мышления;
Воспитательная – воспитывать интерес к математике.
Тип урока: урок проверки и контроля знаний и умений.
Структура урока
Организационный момент (1 мин)
Подготовка к контрольной работе (3 мин)
Контрольная работа (35 мин)
IV.Подведение итогов урока (1 мин)
Ход урока
III. Контрольная работа.
Контрольная работа является итоговым контролем по теме «Показательная функция». Работа состоит из 2 вариантов. Задания записаны на доске.
|
|
Вариант 1 |
Вариант 2 | |
|
1. |
Постройте график функции: | ||
|
|
y = 3x– 1 |
y = 2 – 5x | |
|
2. |
Решите графически уравнение: | ||
|
|
2-х= 3х + 10 |
31-х= 2х – 1 | |
|
3. |
Решите уравнение: | ||
|
|
42х-6– 17 · 4х-3+ 16 = 0 |
52х+10– 6 · 5х+5+ 5 = 0 | |
|
4. |
Решите неравенство: | ||
|
|
|
| |
|
5. |
Решите систему уравнений: | ||
|
|
|
| |
|
6. |
Решите уравнение: | ||
|
|
24х- 310х- 525х= 0 |
49х+ 12х- 316х= 0 | |
Билет № 5.«Логарифмическая функция».
Пусть даны два числовых мн-ва Xи У, и задано некоторое отобр-иеf.
Если каждому элементу![]() соответствует
единственное значение
соответствует
единственное значение![]() и
при этом каждому значению у поставлено
в соответствие единственное зн-ие х, то
говорят, что между мн-вами Х и У установлено
ВОС, кот-ое и наз-сяфункцией.
и
при этом каждому значению у поставлено
в соответствие единственное зн-ие х, то
говорят, что между мн-вами Х и У установлено
ВОС, кот-ое и наз-сяфункцией.
Ф-ция, заданная формулой у=![]() (a>0,a≠1,x>0), называетсялогарифмической ф-циейс
основанием а.
(a>0,a≠1,x>0), называетсялогарифмической ф-циейс
основанием а.
Основные св-ва логарифмической ф-ции:
10. Обл. определения – множествоR+положительных чисел. (0; +∞)
20.Обл. значений – мн-во всех действительных чисел.(-∞; +∞)
30.Приa>1ф-ция возрастает на всей обл. определения; при 0<a<1 ф-ция убывает.
Док-во:
Рассмотрим, a>1 - ф-ция
возрастает. Пусть х1и х2–
произвольные положительные числа и х1< х2. Надо доказать, что![]() Предположим противное, что
Предположим противное, что![]() (*)
Т.к. показательная ф-ция у=ахвозрастает приa>1, то из
неравенства (*) →
(*)
Т.к. показательная ф-ция у=ахвозрастает приa>1, то из
неравенства (*) →![]() (**)
, но по опр. логарифма
(**)
, но по опр. логарифма![]()
![]() т.е. неравенство (**) означает, что х1≥ х2, а это противоречит предположению.
Аналогично для убывающей.
т.е. неравенство (**) означает, что х1≥ х2, а это противоречит предположению.
Аналогично для убывающей.
40.График лог. ф-ции проходит ч/з точку (1; 0).
у=![]() ,
a>1 у=
,
a>1 у=![]() ,
0<a<1
,
0<a<1
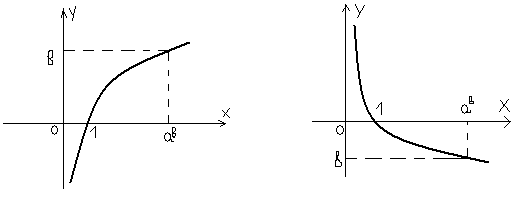
50. Знакопостоянство:
еслиa>1, то у>0, х![]() (1; +∞) и у<0,x
(1; +∞) и у<0,x![]() (0; 1);
(0; 1);
если 0<a<1,
то у>0, х![]() (0; 1) и у<0,x
(0; 1) и у<0,x![]() (1; +∞).
(1; +∞).
60. Логарифмическая ф-ция
у=![]() и показательная ф-ция у=ах, гдеa>0,a≠1,
взаимно обратны. Их графики, имеющие
одинаковое основание, симметричны
относительно прямой у=х.
и показательная ф-ция у=ах, гдеa>0,a≠1,
взаимно обратны. Их графики, имеющие
одинаковое основание, симметричны
относительно прямой у=х.
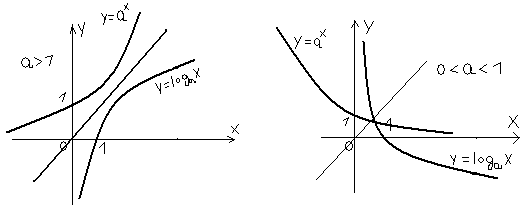
Основные св-ва логарифмов:
10.![]()
20.![]()
30.![]()
40.![]()
Док-во: (логарифм произведения равен сумме логарифмов)
Воспользуемся основным лог. тождеством:
![]() .
Перемножая почленно эти равенства,
получаем:
.
Перемножая почленно эти равенства,
получаем:![]() следовательно, по опр. логарифма
следовательно, по опр. логарифма![]()
50.![]()
60.![]() - формула перехода от одного основания
к другому
- формула перехода от одного основания
к другому
70.![]() (b>0,a>0,a≠1)- основное лог. тождество.
(b>0,a>0,a≠1)- основное лог. тождество.
Логарифмическая ф-ция непрерывна и
является дифференцируемой, т.е. её можно
разложить в степенной ряд. Т.к. ф-ция
![]() непрерывна
в точке х=0 и её произведения в этой точке
не существует, то рассмотрим ф-цию
непрерывна
в точке х=0 и её произведения в этой точке
не существует, то рассмотрим ф-цию![]() .
Рассмотрим ряд Тейлора:
.
Рассмотрим ряд Тейлора:![]() ,
это частный случай, когда х0=0 (ряд
Макларена).
,
это частный случай, когда х0=0 (ряд
Макларена).
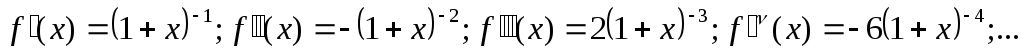
![]() ;
;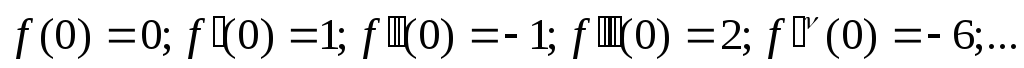
![]() →
→![]()
МЕТОДИКА 5. Методы мотивации изучения темы:
Необходимое условие для создания у учащихся интереса к содержанию обучения и к самой учебной деятельности — возможность проявить в учении умственную самостоятельность и инициативность. Чем активнее методы обучения, тем легче заинтересовать ими учащихся. Основное средство воспитания устойчивого интереса к учению — использование таких вопросов и заданий, решение которых требует от учащихся активной поисковой деятельности.
•Большую роль в формировании интереса к учению играет создание проблемной ситуации, столкновение учащихся с трудностью, которую они не могут разрешить при помощи имеющегося у них запаса знаний; сталкиваясь с трудностью, они убеждаются в необходимости получения новых знаний или применения старых в новой ситуации.. Интересна только та работа, которая требует постоянного напряжения. Легкий материал, не требующий умственного напряжения, не вызывает интереса. Преодоление трудностей в учебной деятельности — важнейшее условие возникновения интереса к ней. Трудность учебного материала и учебной задачи приводит к повышению интереса только тогда, когда эта трудность посильна, преодолима, в противном случае интерес быстро падает.
Учебный материал и приемы учебной работы должны быть достаточно (но не чрезмерно) разнообразны. Разнообразие обеспечивается не только столкновением учащихся с различными объектами в ходе обучения, но и тем, что в одном и том же объекте можно открывать новые стороны. Один из приемов возбуждения у учащихся познавательного интереса — «отстранение», т. e. показ учащимся нового, неожиданного, важного в привычном и обыденном. Новизна материала — важнейшая предпосылка возникновения интереса к нему. Однако познание нового должно опираться на уже имеющиеся у школьника знания. Использование прежде усвоенных знаний — одно из основных условий появления интереса. Существенный фактор возникновения интереса к учебному материалу - его эмоциональная окраска, живое слово учителя.
Эти положения, сформулированные С. М. Бондаренко, могут служит определенной программой организации учебного процесса, специально направленной на формирование интереса.
Основные типы математических задач по теме
- найти область определения функции;
- построить график функции;
- найти область значения функции;
- найти промежутки знакопостоянства функции;
- исследовать функцию и построить ее график;
- найти наибольшее и наименьшее значение функции;
- найти значение выражения.
Типичные ошибки и затруднения изучения темы
Математические ошибки:
вычислительные ошибки: при решении уравнений и неравенств, при нахождении значений функции, при действиях со степенями;
логические ошибки: в выполнении тождественных преобразований, в использовании свойств логарифмов, при определении понятий, при выводе формул;
графические ошибки: при построении графиков функций (не учитывают свойства функций); неправильно применяют преобразование графиков.
3. методы и приемы работы учащихся с учебником математики в соответствии с возрастными особенностями учащихся.
В 5-6 классах используют следующие методы работы с учебником:
1. чтение правил, определений, формулировок теорем учащимися после объяснения учителя
2. чтение вслух учителя ученикам с выделением главного и существенного
3. работа с формулами и иллюстрациями на обложке учебника
4. чтение учебника учащимися и ответы на вопросы учителя
В 7-8 классах добавляются следующие методы работы с учебником:
1. чтение текстов после их объяснения учителем
2. чтение текста учащимися и разбивка его на смысловые абзацы
3. чтение текста из учебника учащимися и запись основных предложений темы по плану, предложенному учителем
В 9 – 11 классах ко всему предложенному добавляется:
1. разбор примеров учащимися в учебнике, после объяснения темы учителем
2. чтение текста учащимися и запись опорного конспекта по данному тексту
3. чтение текста учебника и самостоятельное составление учащимися плана по данному тексту.
4. чтение текста учебника и ответ учащегося по самостоятельно составленному плану
Фрагмент урока изучения новой темы: «Логарифмическая функция».
Цели урока:
Образовательные: обеспечить в ходе урока усвоения понятия логарифмическая функция, формировать умения определять свойства логарифмических функций, формировать умение изображать графики логарифмической функции.
Развивающие: способствовать развитию мышления, восприятия, памяти, воображению, внимания.
Воспитательные: воспитывать устойчивый интерес к математике, воспитывать отдельные качества личности: аккуратность, настойчивость, трудолюбие.
Тип урока: изучение нового материала
Структура урока:
организационный момент
постановка целей урока
проверка домашнего задания
подготовка к изучению нового материала
изучение нового материала
первичное закрепление и осмысление нового материала
постановка домашнего задания
подведение итогов урока.
|
Действия учителя |
Действия учеников | ||||||||||||||||||||
|
ответьте на вопрос 1. что называется функцией? 2. какие функции вы узнали в этом году? 3. какие свойства функций вы знаете? 4. что называется графиком функции?
Сегодня мы изучим новую функцию логарифмическую. Когда мы изучали показательную функцию, мы оформляли ее свойства в таблицу. Сейчас я предлагаю открыть вам страницу 98 в ваших учебниках прочитать параграф 18 и записать в тетрадях опорный конспект по плану предложенному на доске. Опорный конспект вы будите оформлять так же, как оформляли при изучении показательной функции. План опорного конспекта.
А теперь к доске я приглашаю одного человека который оформит правильно конспект на доске.
|
Ответы: Функцию, заданную формулой у=logах, где а>0, а≠0 называют логарифмической функцией с основанием а.
| ||||||||||||||||||||
Билет № 6.«Тригонометрические функции».
Синус, косинус, тангенс и котангенс называют основными тригонометрическими функциями.
Опр. Ф-ции, заданные формуламиy=sinxиy=cos x, называются соответственносинусомикосинусом.
Св-ва синуса и косинуса:
D(y)=(-∞;+∞).
E(y)=[-1;1].
y=cosx– чётная ф-ция, т.е.cos(-x)=cosx
y=sinx– нечётная ф-ция, т.е.sin(-x)= -sinx
y=sinxиy=cosxявл-ся периодическими и наименьший положительный период равен
 .
.
cos (x+![]() )=
cos x, sin (x+
)=
cos x, sin (x+![]() )=
sin x (n
)=
sin x (n![]() z).
z).
Док-во:
Пусть Т – произвольный положительный
период косинуса, то
![]() при любом α.
при любом α.
Полагая, что
![]() ,
находим
,
находим![]() Наименьшее
положительное число Т, для которогоcosx=1, есть
Наименьшее
положительное число Т, для которогоcosx=1, есть![]() .
.
Пусть Т – произвольный положительный
период синуса, то
![]()
Полагая, что
![]() ,
находим
,
находим![]() Ноsinx=1 только при
Ноsinx=1 только при![]() .
Поэтому Т=2
.
Поэтому Т=2![]() .
Наименьшее положительное число 2
.
Наименьшее положительное число 2![]() есть
есть![]() .
.
5)y=sinxвозрастает на![]() и убывает на
и убывает на![]()
y=cosxвозрастает на![]() и убывает на
и убывает на![]()
6)графики:
y=sin x y=cos x
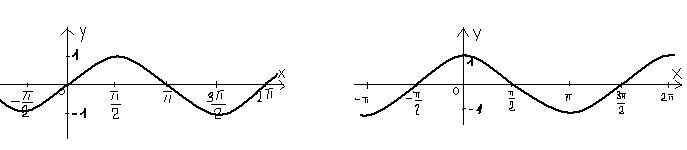
Опр. Ф-ции, заданные формуламиy=tgxиy=ctg x, называются соответственнотангенсомикотангенсом.
Св-ва тангенса и котангенса:
1.)D(tg)
все числа х для которыхcosx≠0, т.е. х≠![]() (n
(n![]() z).
z).
D(сtg) все
числа х для которыхsinx≠0, т.е. х≠![]() (n
(n![]() z).
z).
2.)E(y) – вся числовая прямая.
3.)y=tgxиy=сtgx– нечётные ф-ции, т.е.tg(-x)= -tgх; сtg(-x)= - сtgх;
4.)y=tgxиy=сtgxявл-ся периодическими и наименьший
положительный период равен![]() .
.
tg (x+![]() )=
tg x, сtg (x+
)=
tg x, сtg (x+![]() )=
сtg x (n
)=
сtg x (n![]() z).
z).
Док-во:
Пусть Т – произвольный положительный
период тангенса, то
![]() .
Т.к. на интервале
.
Т.к. на интервале![]() тангенс нулей не имеет,
тангенс нулей не имеет,![]() .
А
.
А![]() -
это период ф-ции тангенс и значит
-
это период ф-ции тангенс и значит![]() -
это наименьший положительный период
тангенса. Дляy=сtgxдок-во аналогичное.
-
это наименьший положительный период
тангенса. Дляy=сtgxдок-во аналогичное.
5.)y=tgxвозрастает на![]() ,
аy=сtgxубывает на
,
аy=сtgxубывает на![]() .
.
6.)графики:
y=tgxy=сtgx
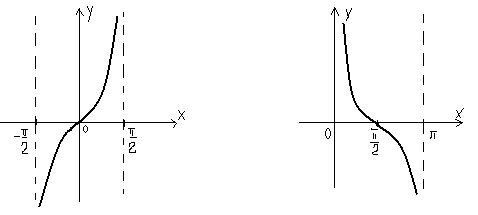
Ф-ции синус и косинус непрерывны на всей обл. определения, а значит дифференцируемы. Рассмотрим разложения функций в степенной ряд.
f(x)=sinx
Рассмотрим ряд Тейлора:
![]() ,
это частный случай, когда х0=0 (ряд
Маклорена).
,
это частный случай, когда х0=0 (ряд
Маклорена).

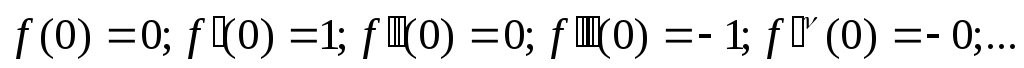
![]() →
→![]()
y=cosxразлаживается аналогично:
![]()
![]()
МЕТОДИКА 6. Фрагмент урока изучения нового материала
Цели урока:
Обучающая– ввести определения тригонометрических функций и научить строить их графики;
Развивающая – развитие познавательных процессов, общеучебных умений;
Воспитательная– воспитание интереса к математике, аккуратность.
Ход урока
|
Деятельность учителя |
Деятельность учащихся |
|
1.«Давайте вспомним: Что такое функции? (из курса алгебры 9 кл) Будет ли функцией y=sinx и y=cosx ?
2. Тема урока: Тригонометрические функции y=sinx, y=cosx. Кратко рассказывает о работе на данном уроке.
3. Объяснение нового материала, а именно: - определение единичной окружности; - определение функций синус и косинус; - область определения функций y=sinx, y=cosx; - область значений функций синус и косинус; - чётность и нечётность функций; - периодические функции; - промежутки, на которых функция принимает положительные значения; - промежутки, на которых функция принимает отрицательные значения; - наибольшее значение, равное 1; - наименьшее значение равное -1.
4. Строим график функции синус на отрезке [0;2п]. График синуса называется синусоидой. Строим график функции косинус, используя cosx = sin(x+п/2). (параллельный перенос графика синус на расстояние п/2 в отрицательном направлении оси ОХ, рис.9).
5. Построить график функции: 1) y=3sinx 2) y=(1/2) sinx
|
Слушают, отвечают на вопросы, работают с учителем.
Слушают учителя.
Слушают, делают записи в тетрадях, работают с учителем по учебнику.
Строят графики в тетрадях с помощью линейки и карандаша.
Занимаются решением и построением графика.
|
Средства наглядности: таблицы, мультимедийный проектор, компьютер.
Создание проблемной ситуации (например: Как построить функцию?).
Билет № 7. «Производная».
Рассмотрим на мн-ве Х ф-цию у=f(x),
выберем внутреннею (.)х0этого
мн-ва (т.е. если![]() такая окрестность (.)х0, которая
целиком
такая окрестность (.)х0, которая
целиком![]() мн-ву Х) и найдём
мн-ву Х) и найдём![]() .
Дадим х0приращение
.
Дадим х0приращение![]() ,
получим новое значение аргумента
,
получим новое значение аргумента![]() ,
вычислим
,
вычислим![]() .
Составим разность, которую назовём
приращением ф-ции и обозначим
.
Составим разность, которую назовём
приращением ф-ции и обозначим![]() :
:![]() .Составим
отношение приращения ф-ции к приращению
аргумента и вычислим предел отношения
.Составим
отношение приращения ф-ции к приращению
аргумента и вычислим предел отношения![]() при
при![]()
Производной ф-цииу=f(x)в (.) х0наз. конечный
предел отношения приращения ф-ции к
вызвавшему его приращению аргумента,
при![]() Т.е.
Т.е.![]() .
.
Если приращение ф-ции в (.)х0м/б
представлено в виде![]() ,
то ф-циюу=f(x)наз. дифференцируемойв (.)
х0, где
,
то ф-циюу=f(x)наз. дифференцируемойв (.)
х0, где![]() -
это число не зависящее от
-
это число не зависящее от![]() (производная),
(производная),![]() -
это бесконечно малая величина
-
это бесконечно малая величина![]() при
при![]()
Выражение
![]() наз.дифференциалом ф-цииу=f(x)в (.) х0.
наз.дифференциалом ф-цииу=f(x)в (.) х0. ![]() или
или![]() ,
где
,
где![]() -
приращение независимой переменной.
-
приращение независимой переменной.