Перевод числа из десятичной системы счисления в q-ичную

Описанный выше алгоритм нахождения q-чных цифр на практике реализуют в виде последовательного деления в столбик.

П

_5709 |9

54 _634|9

_ 30 63 _– 70 |9

27 4 63 7

_ 39 7

36

3

ример:Найти запись числа 5709 в девятиричной системе счисления.

Оформим вышеописанный процесс в виде деления в столбик: 5709 = 7743₉ .

Перевод числа из десятичной системы счисления в произвольную q-чную легко программируется: все вычисления осуществляются в одном цикле.

Перевод числа из q-чной системы счисления в десятичную (схема Горнера)

Если k = ()_q , то k = a_nqⁿ + a_n–1q^n–1 + … + a₁q + a₀ = = ((…((a_nq + a_n–1)q + a_n–2)q … )q + a₁)q + a₀ . Таким образом, процесс нахождения десятичной записи числа k можно организовать рекуррентно, полагая 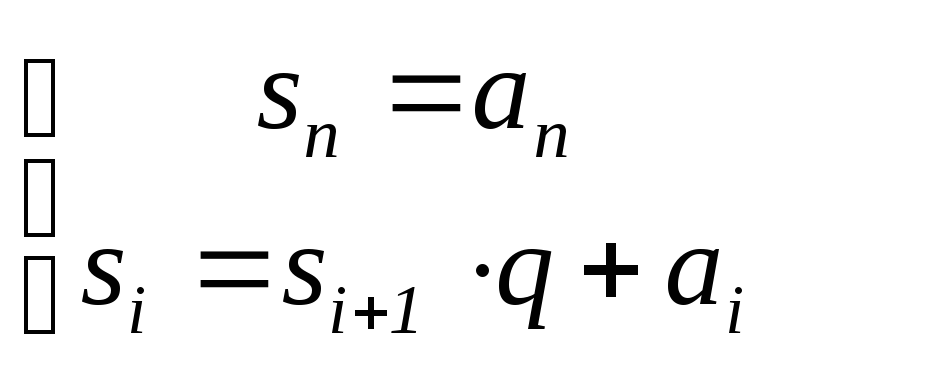(n–1  i  0). Записывая каждое s_i в десятичной системе счисления, в результате получим десятичную запись числа k = s₀ . Описанный выше процесс вычислений называется схемой Горнера.

Пример: Найти десятичную запись числа 1С8D₁₆ . Оформим процесс вычислений по схеме Горнера в виде таблицы:

i	3	2	1	0
ai	1	12	8	13
si	1	28 = 116+12	456 = 2816+8	7309 = 45616+13

Таким образом, 1С8D₁₆ = 7309₁₀ .

Следует отметить, что схему Горнера можно применять для вычисления любых полиномиальных выражений вида a_nxⁿ + a_n–1x^n–1 + … + a₁x + a₀ , где a_i (0  i  n) и x – числа, матрицы и другие математические объекты, которые можно складывать и умножать.

Перевод числа из одной системы счисления в другую

В общем случае, для перевода числа из p-ичной системы счисления в q-чную вначале переводят его из p-чной системы в десятичную, а полученный результат затем переводят в q-чную систему счисления.

Вычисления упрощаются, если основание одной системы счисления равно некоторой степени основания другой системы. Так, если p = q^s, то для перевода числа k = a_nq^sn + a_n–1q^sn–1 + … + a₁q^s + a₀ в q-ичную систему достаточно перевести в эту систему каждую цифру a_i , найдя её разложение a_i = b_{i s–1}q^s–1 + … + b_{i 1}q + b_{i 0} по степеням q, и записать искомый результат k = , отбросив незначащие нули в старших разрядах.

Примеры: 1. (24)5₂₇ = 2427 + 5 = (23² + 23 + 0)3³ + (03² + 13 + 2) = = 23⁵+23⁴+03³+03²+13+2 = 220012₃ .

2. AC0F₁₆ = (24 + 2)4⁶ + (34)4⁴ + (34 + 3) = 24⁷ + 24⁶ + 34⁵ + 04⁴ + + 04³ + 04² + 34 + 3 = 22300033₄ = (10)(10)(11)(00)(00)(00)(11)(11)₂ = = 1010110000001111₂ .

Если же q = p^s , то цифры числа k = нужно разбить, двигаясь справа налево, на группы поs цифр в каждой и полученные p-чные числа рассматривать в качестве цифр данного числа в q-чной системе счисления.

Пример: 10101110010₂ = 010.101.110.010₂ = 2562₈ = 0101.0111.0010₂ = = 572₁₆ = (01)(01)(01)(11)(00)(10)₂ = 111302₄ .