
- •Министерство образования и науки Российской Федерации
- •Глава I. Азы теории чисел
- •§ 1. Деление целых чисел с остатком
- •5709 Mmmmmdссiiiiiiiii,
- •Перевод числа из десятичной системы счисления в q-ичную
- •Перевод числа из q-чной системы счисления в десятичную (схема Горнера)
- •Перевод числа из одной системы счисления в другую
- •Арифметические действия в позиционных системах счисления
- •§ 2. Деление целых чисел нацело
- •Свойства делимости нацело
- •§ 3. Наибольший общий делитель и наименьшее общее кратное
- •Основные свойства наибольшего общего делителя и наименьшего общего кратного
- •§ 4. Алгоритм Евклида
- •Расширенный алгоритм Евклида
- •§ 5. Взаимно простые числа
- •Простейшие свойства взаимно простых чисел
- •§ 6. Простые числа
- •Простейшие свойства простых чисел
- •§ 7. Простые числа в арифметических прогрессиях
- •О распределении простых чисел
- •§ 8. Язык сравнений
- •Свойства сравнений
- •§ 9. Функция Эйлера
- •§ 10. Теоремы Эйлера и Ферма
- •§ 11. Признаки делимости
- •§ 12. Принцип Дирихле
- •Глава II. Некоторые диофантовы уравнения
- •§ 1. Линейные диофантовы уравнения
- •§ 2. Общее диофантово уравнение от одного переменного
- •§ 5. Пифагоровы тройки
- •§ 6. Уравнение Ферма-Пелля
- •Глава III. Великая теорема ферма и abc – проблема
- •§ 1. Великая теорема Ферма
- •§ 2. Методы Эйлера-Куммера доказательства Великой теоремы Ферма
- •§ 3. Гипотеза Таниямы и доказательство Великой теоремы Ферма
- •§ 4. Abc – Теорема для многочленов и её следствия
- •§ 5. Abc – Гипотеза для натуральных чисел
- •§ 6. Некоторые следствия из abc– гипотезы
- •Глава IV. Задача о счастливых билетах
- •§ 1. Сведение задачи к задаче о числе наборов цифр с заданной суммой компонент
- •§ 2. Задача о числе наборов цифр с заданной суммой компонент
- •§ 3. Ещё одно решение задачи о числе наборов цифр с заданной суммой компонент
§ 2. Методы Эйлера-Куммера доказательства Великой теоремы Ферма
Уже доказательство Великой теоремы Ферма для показателя n = 3 не элементарно. Впервые полученное Эйлером, оно в течение многих лет оставалось идейным источником для дальнейших обобщений и модификаций.
Идея проста: если x3 + y3 = z3 для целых x, y, z, не равных нулю, то
z3 = (x + y)(x2 – xy + y2) = (x + y)(x – y)(x + 2y),
где
=
![]() , 2
=
, 2
= ![]() =
– 1 , а
3
= –1. Таким
образом, z3
разложено
в произведение трёх множителей из
множества чисел K
= {z
= p
+ q
C
| p,
q
Z
}. Легко
проверить, что это множество замкнуто
относительно сложения, вычитания и
умножения:
=
– 1 , а
3
= –1. Таким
образом, z3
разложено
в произведение трёх множителей из
множества чисел K
= {z
= p
+ q
C
| p,
q
Z
}. Легко
проверить, что это множество замкнуто
относительно сложения, вычитания и
умножения:
(p + q) ± (r + s) = (p ± r) + (q ± s) K ,
(p + q)(r + s) = pr + (qr + ps) + 2qs =
= pr + (qr + ps) + ( – 1)qs = (pr – qs) + (qr + ps + qs) K .
Такие подмножества в C называют числовыми кольцами. В них можно производить вычисления почти как с целыми числами.
Как известно, любое
целое число единственным образом
раскладывается в произведение простых:
z
=
![]() ,
где
{–1, +1}, pi
– простые
числа, i
N
(1
i
k).
Отсюда следует, что если произведение
нескольких попарно взаимно простых
целых чисел является m-й
степенью некоторого целого числа, то
каждый из сомножителей (с точностью до
знака) является m-й
степенью целого числа. Действительно,
если tm
= u1…uk
, то имеет
место разложение в натуральных числах:
|t|m
= |u1|…|uk|,
где сомножители попарно взаимно просты:
НОД(|ui|,
|uj|)
= 1. Это
значит, что в канонических разложениях
чисел |u1|,
… , |uk|
нет одинаковых
простых чисел, а показатель степени
каждого простого числа делится на m,
т.к. этот показатель является показателем
степени этого же простого числа в |t|m.
Итак, |ui|
= vim
(1
i
k)
и |t|
= v1
… vk
для некоторых
натуральных чисел v1
, … , vk
.
,
где
{–1, +1}, pi
– простые
числа, i
N
(1
i
k).
Отсюда следует, что если произведение
нескольких попарно взаимно простых
целых чисел является m-й
степенью некоторого целого числа, то
каждый из сомножителей (с точностью до
знака) является m-й
степенью целого числа. Действительно,
если tm
= u1…uk
, то имеет
место разложение в натуральных числах:
|t|m
= |u1|…|uk|,
где сомножители попарно взаимно просты:
НОД(|ui|,
|uj|)
= 1. Это
значит, что в канонических разложениях
чисел |u1|,
… , |uk|
нет одинаковых
простых чисел, а показатель степени
каждого простого числа делится на m,
т.к. этот показатель является показателем
степени этого же простого числа в |t|m.
Итак, |ui|
= vim
(1
i
k)
и |t|
= v1
… vk
для некоторых
натуральных чисел v1
, … , vk
.
Если предположить, что аналогичный факт имеет место для числового кольца K, то Великая теорема Ферма доказывается просто. Из разложения z3 = (x + y)(x + y)(x – 2y) и попарной взаимной простоты целых чисел x, y, z следует, что взаимно просты и множители в этом разложении. Действительно, если, например x + y, x – 2y делятся на некоторое простое в K число π = p + q, то
x + x = (1 + )x = (x + y) + (x – 2y) π ,
–y + 2y = (2 – 1)y = (1 + )y = (x + y) – (x – 2y) π ,
что невозможно: если x + x = (p +q)(k + l), y = (p +q)(m + n).
§ 3. Гипотеза Таниямы и доказательство Великой теоремы Ферма
1. Эллиптические
кривые. Эллиптической
кривой назовём
кривую на
плоскости, заданную уравнением y2
= x3
+ ax2
+ bx
+ c,
где a,
b,
c
Q
. Правая
часть этого уравнения представляет
собой кубический многочлен, который
можно с помощью замены x
= z
–
![]() всегда можно преобразовать к приведённому
виду z3
+ pz
+ q
:
всегда можно преобразовать к приведённому
виду z3
+ pz
+ q
:
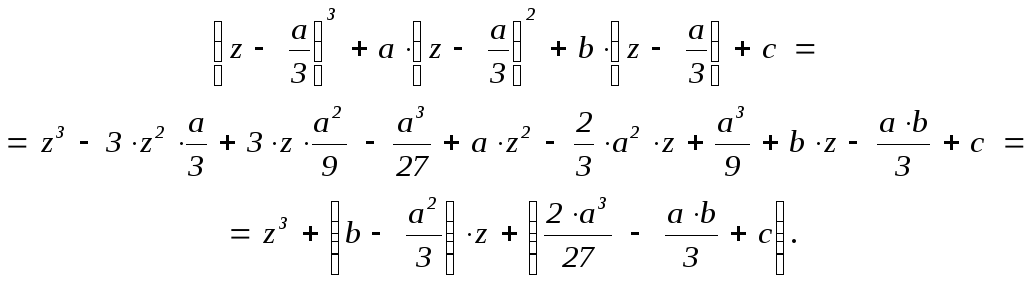
Таким образом,
![]() .
Сама же эллиптическая кривая преобразуется
кстандартному
виду: y2
= z3
+ pz
+ q
(p,
q
Q).
.
Сама же эллиптическая кривая преобразуется
кстандартному
виду: y2
= z3
+ pz
+ q
(p,
q
Q).
Известно, что один из корней кубического уравнения z3 + pz + q = 0 может быть найден по формуле Кардано:
![]() .
.
При этом величина
![]() называетсядискриминантом
приведённого
кубического уравнения
z3
+ pz
+ q
= 0.
Он равен нулю тогда и только тогда,
когда это кубическое уравнение имеет
кратный корень. Если в выражение для
дискриминанта подставить
называетсядискриминантом
приведённого
кубического уравнения
z3
+ pz
+ q
= 0.
Он равен нулю тогда и только тогда,
когда это кубическое уравнение имеет
кратный корень. Если в выражение для
дискриминанта подставить
![]() ,
то получим дискриминант общего
кубического уравнения:
,
то получим дискриминант общего
кубического уравнения:
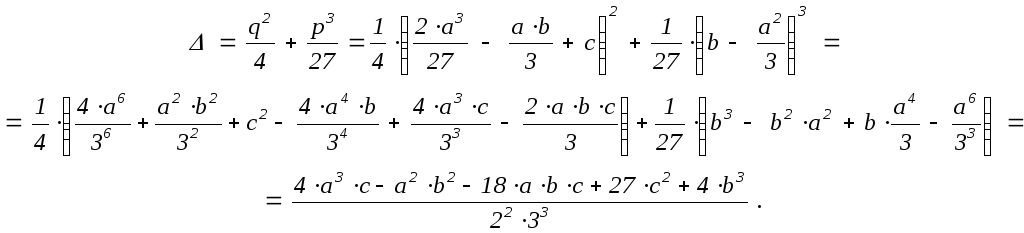
По аналогии с дискриминантом кубического уравнения введём дискриминант D эллиптической кривой y2 = x3 + ax2 + bx + c (a, b, c Q), полагая D = –16(4a3c – a2b2 – 18abc + 27c2 + 4b3). Отличие в числовом множителе от дискриминанта здесь не принципиально, а приведение к общему знаменателю удобно тем, что при целых a и b дискриминант тоже будет целым числом.
2. Особые точки эллиптической кривой. Как правило, рассматриваются кривые с ненулевым дискриминантом, т.к. если дискриминант нулевой, то у кривой есть особенности: точки самопересечения и возврата. Приведённый ниже рисунок даёт представление о неособых эллиптических кривых и кривых с особенностями. Кстати, если D > 0, то эллиптическая кривая состоит из двух связных “кусков”, а если D < 0, то из одного. Это объясняется тем, что при D > 0 многочлен x3 + ax2 + bx + c имеет три вещественных корня, вблизи которых этот многочлен меняет знак. Значит, эллиптическая кривая y2 = x3 + ax2 + bx + c на отрезке отрицательности многочлена между двумя соседними корнями не имеет действительных точек (корень из отрицательного числа не извлекаем).

Более точно,
эллиптическая кривая y2
= x3
– ax2
– bx
– c
называется неособой,
если не имеет решений следующая система
уравнений для многочлена f(x,
y)
= y2
– x3
– ax2
– bx
– c
:
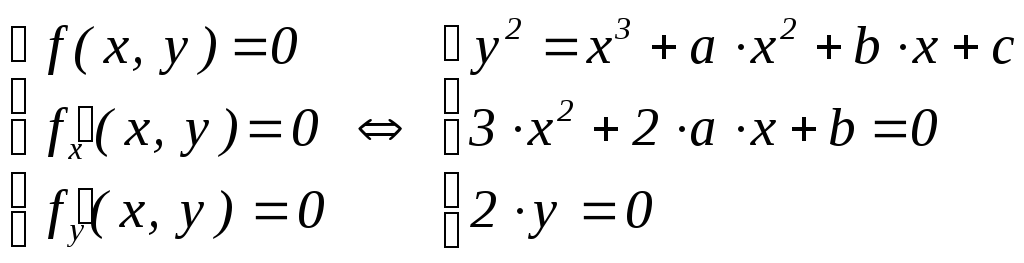 .Если решения
(x
; y)
этой системы
существуют, то соответствующая точка
M(x
; y)
эллиптической кривой называется
особой.
Последние два уравнения системы
показывают, что многочлен x3
– ax2
– bx
– c
имеет общий корень со своей производной,
т.е. имеет кратный корень, а значит, его
дискриминант нулевой. Поскольку этот
дискриминант отличается лишь множителем
от дискриминанта соответствующей
эллиптической кривой, то особые точки
существуют лишь у кривых с нулевым
дискриминантом. Обратно, из рассматриваемой
системы видно, что любая точка M(x0
; 0), где x0
– кратный
корень многочлена x3
– ax2
– bx
– c
(который существует в случае обращения
его дискриминанта в ноль) является
особой точкой кривой. Поскольку
кубический многочлен имеет либо один
двукратный корень, либо один трёхкратный,
либо же вообще не имеет кратных корней,
то на эллиптической кривой может быть
не более одной особой точки.
.Если решения
(x
; y)
этой системы
существуют, то соответствующая точка
M(x
; y)
эллиптической кривой называется
особой.
Последние два уравнения системы
показывают, что многочлен x3
– ax2
– bx
– c
имеет общий корень со своей производной,
т.е. имеет кратный корень, а значит, его
дискриминант нулевой. Поскольку этот
дискриминант отличается лишь множителем
от дискриминанта соответствующей
эллиптической кривой, то особые точки
существуют лишь у кривых с нулевым
дискриминантом. Обратно, из рассматриваемой
системы видно, что любая точка M(x0
; 0), где x0
– кратный
корень многочлена x3
– ax2
– bx
– c
(который существует в случае обращения
его дискриминанта в ноль) является
особой точкой кривой. Поскольку
кубический многочлен имеет либо один
двукратный корень, либо один трёхкратный,
либо же вообще не имеет кратных корней,
то на эллиптической кривой может быть
не более одной особой точки.
Чем отличаются особые точки возврата от точек самопересечения ? Точка возврата M(x0 ; 0) характеризуется тем, что x0 – кратный корень многочлена x3 + ax2 + bx + c, а сама точка является “крайней” на кривой. Это значит, что вблизи неё многочлен x3 + ax2 + bx + c = (x – x0)2(x – x1) меняет знак, т.е. x1 = x0 . Таким образом, многочлен x3 + ax2 + bx + c имеет трёхкратный корень x0 тогда и только тогда, когда M(x0 ; 0) – точка возврата соответствующей эллиптической кривой. Имеем:
x3 + ax2 + bx + c = (x – x0)2(x – x1)
(a = –(x1 + 2x0), b = x02 + 2x0x1 , c = –x02x1).
Поэтому x1 = x0 (x1 – x0)2 = 0 (x1 + 2x0)2 = 3(x02 + 2x0x1) a2 = 3b. Итак, особая точка M(x0 ; 0) на эллиптической кривой с нулевым дискриминантом является точкой возврата тогда и только тогда, когда a2 = 3b. В случае a2 3b особая точка M(x0 ; 0) будет точкой самопересечения. Других особых точек у эллиптической кривой нет.
3. Редукция
эллиптической кривой по простому модулю.
Для любого простого числа p
и целых a,
b,
с
Z
можно рассмотривать эллиптическую
кривую y2
= x3
+ ax2
+ bx
+ c
“по модулю p”,
т.е. изучать множество решений сравнения
y2
x3
+ ax2
+ bx
+ c
(mod
p).
Пусть np
– количество
решений этого сравнения, т.е. количество
пар целых чисел (r
; s),
где 0
![]() <p,
и s2
r3
+ ar2
+ br
+ c
(mod
p).
Ясно, что если для некоторого простого
p
рассматриваемое сравнение не имеет
решений, т.е. np
= 0, то на
исходной эллиптической кривой не будет
и целых точек
– целочисленных решений диофантова
уравнения y2
= x3
+ ax2
+ bx
+ c.
<p,
и s2
r3
+ ar2
+ br
+ c
(mod
p).
Ясно, что если для некоторого простого
p
рассматриваемое сравнение не имеет
решений, т.е. np
= 0, то на
исходной эллиптической кривой не будет
и целых точек
– целочисленных решений диофантова
уравнения y2
= x3
+ ax2
+ bx
+ c.
Для эллиптических
кривых “по модулю p”
можно ввести понятие особых
точек: пара
(r
; s),
где 0
![]() <p,
и s2
r3
+ ar2
+ br
+ c
(mod
p)
называется
особой
точкой, если
p
является
делителем множителя 4a3c
– a2b2
– 18abc
+ 27c2
+ 4b3
дискриминанта
D
эллиптической
кривой y2
= x3
+ ax2
+ bx
+ c
и x3
+ ax2
+ bx
+ c
(x
– r)2
(mod
p).
По аналогии с обычными кривыми “точка”
(r
; s)
называется точкой
возврата
тогда и только тогда, когда a2
3b
(mod
p).
В противном случае a2
<p,
и s2
r3
+ ar2
+ br
+ c
(mod
p)
называется
особой
точкой, если
p
является
делителем множителя 4a3c
– a2b2
– 18abc
+ 27c2
+ 4b3
дискриминанта
D
эллиптической
кривой y2
= x3
+ ax2
+ bx
+ c
и x3
+ ax2
+ bx
+ c
(x
– r)2
(mod
p).
По аналогии с обычными кривыми “точка”
(r
; s)
называется точкой
возврата
тогда и только тогда, когда a2
3b
(mod
p).
В противном случае a2
![]() 3b
(mod
p)
особая точка
(r
; s)
называется точкой
самопересечения
рассматриваемой эллиптической кривой
“по модулю p”.
3b
(mod
p)
особая точка
(r
; s)
называется точкой
самопересечения
рассматриваемой эллиптической кривой
“по модулю p”.
Лемма (об особых точках по модулю p). Следующие условия для целых чисел a, b, c эквивалентны:
(1) многочлен x3 + ax2 + bx + c имеет кратный корень по модулю p;
(2) простое число p делит 4a3c – a2b2 – 18abc + 27c2 + 4b3 .
При этом многочлен x3 + ax2 + bx + c имеет трёхкратный корень по модулю p тогда и только тогда, когда
p | (4a3c – a2b2 – 18abc + 27c2 + 4b3), a2 3b (mod p).
Доказательство. (1) (2) Пусть вначале многочлен x3 + ax2 + bx + c имеет кратный корень , т.е.
x3 + ax2 + bx + c (x–)2(x–) = x3–(+2)x2+(2+ 2)x– 2 (mod p).
Значит, a –( + 2), b 2 + 2, c – 2 (mod p), и
4a3c – a2b2 – 18abc + 27c2 + 4b3
4( + 2)3 2 – ( + 2)2(2 + 2)2 – 18( + 2)(2 + 2) 2 +
+ 27 4 2 + 4(2 + 2)3
4 4 2 + 24 3 3 + 48 2 4 + 32 5 –
– ( + 2)(2 + 2)(2 2 + 5 2 + 2 3 + 18 2) +
+ 27 4 2 + 32 3 3 + 48 4 2 + 24 5 + 4 6
4 6 + 56 5 + 123 4 2 + 56 3 3 + 4 2 4 –
– (2 3 + 5 2 + 2 2)(2 3 + 23 2 + 2 2)
4 6 + 56 5 + 123 4 2 + 56 3 3 + 4 2 4 –
– 4 6 – 56 5 – 123 4 2 – 56 3 3 – 4 2 4 0.
(2) (1) Пусть теперь p | (4a3c – a2b2 – 18abc + 27c2 + 4b3). Вначале рассмотрим случаи p = 2, 3.
p = 2: Учитывая, что u2 u (mod 2) для любого u Z, получаем
2 | (4a3c – a2b2 – 18abc + 27c2 + 4b3) 2 | (ab + c).
Таким образом, числа ab и c чётны или нечётны одновременно. Если они оба чётны, то x3 + ax2 + bx + c x3 + ax2 + bx x(x2 + ax + b). При этом либо x2 + ax + b x(x + a) (mod 2), если b 0 (mod 2), и x 0 – двукратный корень по модулю 2, либо же x2 + ax + b x2 + 1 (x + 1)2, если b 1, a 0 (mod 2), и x 1 – двукратный корень по модулю 2, что и требовалось.
p =
3:
Имеем
p
| (a3c
– a2b2
+ b3).
Учитывая,
что u3
u
(mod
3) для любого
u
Z
и u2
1 (mod
3), если u
![]() 0 (mod
3), получаем
0 (mod
3), получаем
3 | (4a3c – a2b2 – 18abc + 27c2 + 4b3) 3 | (ac – a2b2 + b).
Если a
и b
не делятся
на 3,
то (ab)2
1 (mod
3), b
1 – ac
(mod
3). Поскольку
1
– ac
![]() 0,
a
0,
a
![]() 0 (mod 3),
получаем
ac
–1,
b
2,
c
–a (mod 3).
Таким
образом,
x3
+ ax2
+ bx
+ c
x3
+ ax2
+ 2x
– a
(x – a)(x2
+ 2ax
+ 1)
(x – a)(x
+ a)2
,
т.е.
x
–a
(mod
3) – двукратный
корень по модулю 3.
0 (mod 3),
получаем
ac
–1,
b
2,
c
–a (mod 3).
Таким
образом,
x3
+ ax2
+ bx
+ c
x3
+ ax2
+ 2x
– a
(x – a)(x2
+ 2ax
+ 1)
(x – a)(x
+ a)2
,
т.е.
x
–a
(mod
3) – двукратный
корень по модулю 3.
Если a делится на 3, то 3 | (ac – a2b2 + b) 3 | b, и
x3 + ax2 + bx + c x3 + c (x + c)3.
Если
b
0,
a
![]() 0 (mod 3),
то
3
| (ac
– a2b2
+ b)
3 | c,
и
0 (mod 3),
то
3
| (ac
– a2b2
+ b)
3 | c,
и
x3 + ax2 + bx + c x3 + ax2 x2(x + a),
т.е. x 0 – двукратный корень по модулю 3.
Таким образом, лемма доказана для p = 2, 3.
Пусть теперь p 5. Тогда можно найти обратный элемент u Z к 3 по модулю p. Для этого достаточно записать линейное разложение НОД(3, p) = = 1 = pv + 3u и заметить, что 3u 1 (mod p), что и требовалось.
Если a
![]() 0 (mod
3), сделаем
замену x
= z
– ua
и получим:
0 (mod
3), сделаем
замену x
= z
– ua
и получим:
x3 + ax2 + bx + c (z – ua)3 + a(z – ua)2 + b(z – ua) + c
z3 – (3u)az2 + 3u2a2z – u3a3 + az2 – 2ua2z + u2a3 + bz – uba + c
z3 + (– ua2 + b)z + (–u3a3 + u2a3 – uba + c)
z3 + z + µ (mod p),
где = – ua2 + b, µ = –u3a3 + u2a3 – uba + c. При этом
x3 + ax2 + bx + c (x – )2(x – ) (mod p)
z3 + z + µ (z – ua – )2(z – ua – ) (mod p).
Таким образом, достаточно доказать существование кратного корня у редуцированного многочлена z3 + z + µ. Дискриминант этого многочлена равен 27µ2 + 43 27((1–u)u2a3 – uba + c)2 + 4(–ua2 + b)3
27(1–u)2u4a6 + 27u2b2a2 + 27c2 – 54(1–u)u3ba4 + 54(1–u)u2a3c –
– 54ubac – 4u3a6 + 12u2a4b – 12ua2b2 + 4b3
(1–u)2ua6 + 3b2a2 + 27c2 – 2(1–u)ba4 + 6(1–u)a3c – 18abc –
– 4u3a6 + 4ua4b – 4a2b2 + 4b3
(–3u3–2u2+u)a6 – 2(1–3u)a4b – (6u–6)a3c – a2b2 – 18abc+27c2+4b3
(–3u2+u)a6 + 4a3c – a2b2 – 18abc+27c2+4b3
4a3c – a2b2 – 18abc + 27c2 + 4b3 .
Значит, дискриминант редуцированного уравнения делится на p. Поэтому 27µ2 –43 (mod p), т.е. и µ или не делятся на p одновременно.
Если одно из них делится на p, то многочлен z3 + z + µ z3 (mod p) и имеет кратный корень.
Если
![]() 0
0![]() µ (mod
p),
то, как и выше, найдём обратный элемент
s
к 2
по модулю
p:
2s
1 (mod
p).
Тогда
z
–3µs
(mod p) будет
корнем
многочлена:
z3
+ z
+ µ
–27µ3s3
– 3µs
+ µ
43s3µ
– 3µs+µ
sµ
– 3µs
+ µ
–2sµ
+ µ
0 (mod p).
При
этом
µ (mod
p),
то, как и выше, найдём обратный элемент
s
к 2
по модулю
p:
2s
1 (mod
p).
Тогда
z
–3µs
(mod p) будет
корнем
многочлена:
z3
+ z
+ µ
–27µ3s3
– 3µs
+ µ
43s3µ
– 3µs+µ
sµ
– 3µs
+ µ
–2sµ
+ µ
0 (mod p).
При
этом
z3 + z + µ (z + 3µs)z2 – 3µsz2 + z + µ
(z + 3µs)(z2 – 3µsz) + (9µ2s2 + )z + µ
(z + 3µs)(z2 – 3µsz + (9µ2s2 + )) – 3µs(9µ2s2 + ) + µ
(z + 3µs)(z2 – 3µsz + 9µ2s2 + ),
z2 – 3µsz + 9µ2s2 + = (z + 3µs)z – 6µsz + 9µ2s2 + =
= (z + 3µs)(z – 6µs) + 27µ2s2 + (z + 3µs)(z – 6µs),
т.к. 27µ2s2 + –43s2 + – + 0. Таким образом, z –3µs (mod p) является двукратным корнем многочлена z3 + z + µ, что и требовалось.
Наконец, проверим критерий трёхкратного корня. Если
x3 + ax2 + bx + c (x – )3 x3 – 3x2 + 32x – 3 (mod p),
то a – 3 , b 32 (mod p) и a2 92 3(32) 3b (mod p).
Обратно, пусть p | (4a3c – a2b2 – 18abc + 27c2 + 4b3) и a2 3b2 (mod p), то, как доказано выше, x3 + ax2 + bx + c (x – )2(x – ) x3–(+2)x2+(2+ 2)x– 2 (mod p). Значит, a –( + 2) и b 2 + 2, c – 2 (mod p). Поэтому 2 + 4 + 4 2 a2 3b 6 + 3 2 (mod p), т.е. 0 2 – 2 + 2 ( – )2 (mod p), т.е. (mod p), и – трёхкратный корень многочлена по модулю p.
Лемма доказана.
Замечание. Как следует из доказательства леммы, для многочлена x3 + ax2 + bx + c (a, b, c Z) и простого числа p > 3, делящего множитель 4a3c – a2b2 – 18abc + 27c2 + 4b3 дискриминанта, двукратный корень по модулю p можно найти сразу, выполнив обратные замены на всех шагах доказательства: x –3µs – ua, где 3u 1, µ = –u3a3 + u2a3 – uab + c (1 – u)u2a3 – uab + c 2u3a3 – uab + c, = – ua2 + b, 2s 1 (mod p). Исследование кривой по модулям p = 2, 3 трудностей не вызывает.
Пример. Найти двукратные корни многочлена x3 – 5x2 + x – 1 по всем простым модулям.
Здесь 4a3c – a2b2 – 18abc + 27c2 + 4b3 =
= 4(–5)3(–1) – (–5)212 – 18(–5)1(–1) + 27(–1)2 + 413 =
= 500 – 25 – 90 + 27 + 4 = 416 = 2513.
Таким образом, двукратные корни у многочлена есть по модулям p = 2, 13.
p = 2: x3 – 5x2 + x – 1 x3 + x2 + x + 1 x2(x + 1) + x + 1 (x + 1)(x2 + 1) (x + 1)3.
p = 13: Воспользовавшись замечанием, вначале вычислим вспомогательные константы u , , µ , s , где 3u 1, µ = 2u3a3 – uab + c , = – ua2+b, 2s 1 (mod 13). Ясно, что u 9, µ 293(–5)3–91(–5)–1 –21255+44 –(–1)(–3) + 5 2, –9(–5)2 + 1 –9(–1) + 1 –3, s 2 (mod 13).
П оэтому,
как показывает деление в столбик,
двукратным корнем многочленаx3
– 5x2
+ x
– 1 будет
элемент x
–3µs
– ua
–322
– 9(–5)
1 + 6
7 (mod
13). При этом
имеем x3
– 5x2
+ x
– 1
(x
– 7)2(x
– 4).
оэтому,
как показывает деление в столбик,
двукратным корнем многочленаx3
– 5x2
+ x
– 1 будет
элемент x
–3µs
– ua
–322
– 9(–5)
1 + 6
7 (mod
13). При этом
имеем x3
– 5x2
+ x
– 1
(x
– 7)2(x
– 4).
Эллиптическая кривая y2 = x3 + ax2 + bx + c называется полустабильной, если для любого простого делителя p множителя 4a3c – a2b2 – 18abc + 27c2 + 4b3 её дискриминанта D сравнение x3 + ax2 + bx + c 0 (mod p) не имеет трёхкратных корней. Следует отметить, что это сравнение, как хорошо известно, не может иметь более трёх (различных по модулю p) корней. Как доказано в лемме, это значит, что редукция этой кривой по любому простому модулю может иметь только особые точки самопересечения, но не возврата.
Зафиксируем некоторое простое число p делящее дискриминант D эллиптической кривой y2 = x3 + ax2 + bx + c (a, b, c Z). Тогда по модулю p этот дискриминант нулевой.
Примеры: 1. Кривая y2 = x3 не полустабильна: её дискриминант нулевой, т.к. a = b = c = 0, а правая часть имеет трёхкратный корень x = 0 по любому простому модулю.
2. Пусть A, B – взаимно простые целые числа, С = A + B. Тогда эллиптическая кривая y2 = x(x – A)(x – C) полустабильна.
Действительно, уравнение кривой имеет вид y2 = x3 – (A + C)x2 + ACx, а её дискриминант вычисляется так:
D = –16(– (A + C)2(AC)2 + 4(AC)3) = –16(AC)2(A – C)2 = –16A2B2C2.
Поэтому, если p | A2B2C2, то p делит одно из чисел A, B, C, причём два из этих чисел не могут делиться на p ввиду взаимной простоты A и B: например, если A p, C p, то B = (C – A) p – противоречие. Таким образом, корни x 0, x A, x C (mod p) правой части уравнения кривой не могут все быть одинаковыми.
Определим понятие
кондуктора
эллиптической кривой,
ограничившись только важным для
дальнейшего случаем, т.к. общее его
определение требует далеко выходящих
за рамки данного изложения понятий.
Грубо говоря, кондуктор
![]() собирает в одно произведение все простые
числа, участвующие в каноническом
разложении дискриминанта эллиптической
кривой. При этом степень p
, с которой
простое число p
входит в кондуктор, равна 1,
если кривая “по модулю p”
y2
x3
+ ax2
+ bx
+ c
(mod
p)
обладает точкой
самопересечения.
Эта степень p
равна 2,
если p
> 3 и
эллиптическая кривая, рассматриваемая
по модулю p
обладает точкой
возврата.
В случае, если кривая “по модулю p”
неособая, p
совпадает
с показателем, с которым p
входит в
каноническое разложение дискриминанта
D.
Случаи p
= 2, 3
для кривой с особой точкой возврата
исследуются более сложно, но они не
встретятся в дальнейшем.
собирает в одно произведение все простые
числа, участвующие в каноническом
разложении дискриминанта эллиптической
кривой. При этом степень p
, с которой
простое число p
входит в кондуктор, равна 1,
если кривая “по модулю p”
y2
x3
+ ax2
+ bx
+ c
(mod
p)
обладает точкой
самопересечения.
Эта степень p
равна 2,
если p
> 3 и
эллиптическая кривая, рассматриваемая
по модулю p
обладает точкой
возврата.
В случае, если кривая “по модулю p”
неособая, p
совпадает
с показателем, с которым p
входит в
каноническое разложение дискриминанта
D.
Случаи p
= 2, 3
для кривой с особой точкой возврата
исследуются более сложно, но они не
встретятся в дальнейшем.
Примеры: 1. Для кривой y2 = x3 – 57x2 + 800x имеем
D = –16(4a3c–a2b2–18abc+27c2+4b3) =
= – 16(–5728002 + 48003) = 16800249 = 2145472.
Таким образом, N = 257. Остаётся вычислить степени , , .
Рассмотрим кривую
“по модулю 2”:
y2
x3
+ x2
(mod
2). Она имеет
особую точку (0
; 0), которая
является точкой самопересечения, т.к.
a2
![]() 3b
12
3b
12
![]() 30
(mod
2). Поэтому
= 1.
30
(mod
2). Поэтому
= 1.
Рассмотрим кривую
“по модулю 5”:
y2
x3
– 2x2
(mod
5). Она имеет
особую точку (0
; 0), которая
является точкой самопересечения, т.к.
a2
![]() 3b
(–2)2
3b
(–2)2
![]() 30
(mod
5). Поэтому
= 1.
30
(mod
5). Поэтому
= 1.
Наконец, по модулю
7:
“кривая” y2
x3
– x2
+ 2x
x(x
– 4)2
(mod
7) имеет
особую точку (4
; 0), которая
является точкой самопересечения, т.к.
a2
![]() 3b
(–1)2
3b
(–1)2
![]() 32
(mod
7). Поэтому
= 1.
32
(mod
7). Поэтому
= 1.
Таким образом, кондуктор эллиптической кривой y2 = x3 – 57x2 + 800x равен N = 257 = 70.
2. Для кривой y2 = x3 – x + 1 имеем
D = –16(4a3c–a2b2–18abc+27c2+4b3) = – 16(2712 + 4(–1)3) = –2423.
Таким образом, N = 223. Остаётся вычислить степени , .
Рассмотрим кривую “по модулю 2”: y2 = x3 + x + 1 (mod 2). Здесь многочлен x3 + x + 1 не имеет корней по модулю 2, так что по этому модулю рассматриваемая кривая неособая, и = 4.
По модулю 23:
“кривая” y2
= x3
– x
+ 1 (mod
23) особая,
но её особые точки являются точками
самопересечения, т.к. a2
![]() 3b
02
3b
02
![]() 3(–1)
(mod
23).
Поэтому
= 1.
3(–1)
(mod
23).
Поэтому
= 1.
Итак, кондуктор эллиптической кривой y2 = x3 – x + 1 равен N = 2431.
3.
Пусть A,
B
– взаимно
простые целые числа, С
= A
+ B.
Вычислим кондуктор эллиптической
кривой y2
= x(x
– A)(x
– C),
дискриминант которой вычислен ранее:
D
= –16A2B2C2
. Следовательно,
в кондуктор N
войдут
двойка, а также нечётные простые числа,
делящие A2B2C2,
т.е. делящие одно из чисел A,
B,
C:
N
=
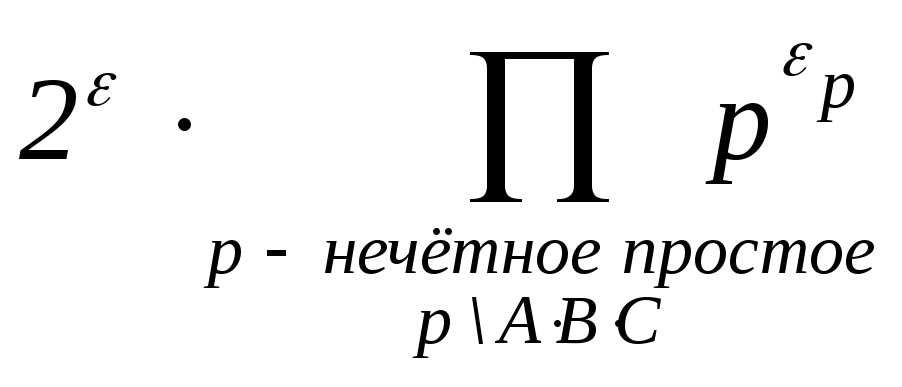 . Вычислим показатели, с которыми эти
простые числа входят в кондуктор. При
этом 2
|
ABC,
т.к. в равенстве A
+ B
= C
все три
числа не могут быть нечётными.
. Вычислим показатели, с которыми эти
простые числа входят в кондуктор. При
этом 2
|
ABC,
т.к. в равенстве A
+ B
= C
все три
числа не могут быть нечётными.
Редукции рассматриваемой кривой по всем простым числам, входящим в кондуктор, особые. Но, как было замечено выше, рассматриваемая кривая полустабильна, т.е. все особенности редукций будут точками самопересечения. По определению, это значит, что = p = 1 для всех p | ABC.
Итак, кондуктор
эллиптической кривой y2
= x(x
– A)(x
– C),
где C
= A
+ B,
НОД(A,
B)
= 1, является
произведением всех простых чисел,
участвующих в каноническом произведении
дискриминанта D
= 16A2B2C2,
т.е. N
=
 .
.
4. Модулярные формы и модулярные эллиптические кривые. Пусть H – верхняя комплексная полуплоскость n N, k Z. Модулярной параболической формой веса k и уровня n называется заданная и дифференцируемая на всём H (аналитическая в H) функция f : H C со следующими свойствами:
![]() ,
,
где a, b, c, d – любые такие целые числа, что ad – bcn = 1, а r Q .
Нетрудно заметить,
что для любого z
H
элемент ![]() при условии ad
– bcn
= 1 тоже
принадлежит H,
так что данное определение корректно.
В самом деле,
при условии ad
– bcn
= 1 тоже
принадлежит H,
так что данное определение корректно.
В самом деле, ![]() , где в знаменателе дроби стоит
положительное число |ncz
+ d|2
, а мнимая часть числителя равна
adIm(z)
– bncIm(z)
= Im(z)
> 0. Таким
образом, рассматриваемая дробь принадлежит
H.
, где в знаменателе дроби стоит
положительное число |ncz
+ d|2
, а мнимая часть числителя равна
adIm(z)
– bncIm(z)
= Im(z)
> 0. Таким
образом, рассматриваемая дробь принадлежит
H.
Множество всех модулярных параболических форм веса k и уровня n обозначим через Sk(n).
Примеры: 1. Нулевая функция 0 : H C является, очевидно, модулярной параболической формой веса k и уровня n.
Если константа является модулярной параболической формой веса k и уровня n, то эта константа равна нулю.
Действительно,
если f(z)
= c,
то из условия ![]() получаем, что
получаем, что ![]() ,
т.е. c
= 0.
,
т.е. c
= 0.
Если f Sk(n), то f Sk(nq) для любого натурального q.
Действительно,
если ad
– bcqn
= 1, то ![]() ввиду условия f
Sk(n),
что и требовалось.
ввиду условия f
Sk(n),
что и требовалось.
Если k – нечётно, то Sk(n) = {0}.
В самом деле, ввиду
(–1)(–1)
– 00
= 1, то из ![]() получаем f(z)
= –f(z),
т.е. f(z)
= 0.
получаем f(z)
= –f(z),
т.е. f(z)
= 0.
Множество Sk(n) модулярных параболических форм веса k и уровня n замкнуто относительно сложения и умножения на комплексные скаляры.
Действительно, если f, g – модулярные параболические формы веса k и уровня n, то они определены на H, значит, для любого z H определены и значения (f + g)(z) = f(z) + g(z) и (f)(z) = f(z). Далее, из дифференцируемости (аналитичности) f и g в H и теорем о дифференцируемости суммы, произведения функций и производной константы следует дифференцируемость функций (f + g)(z) = f(z) + g(z) и (f)(z) = f(z): (f + g)(z) = f(z) + g(z) и (f)(z) = f(z).
Кроме того, выполнены условия
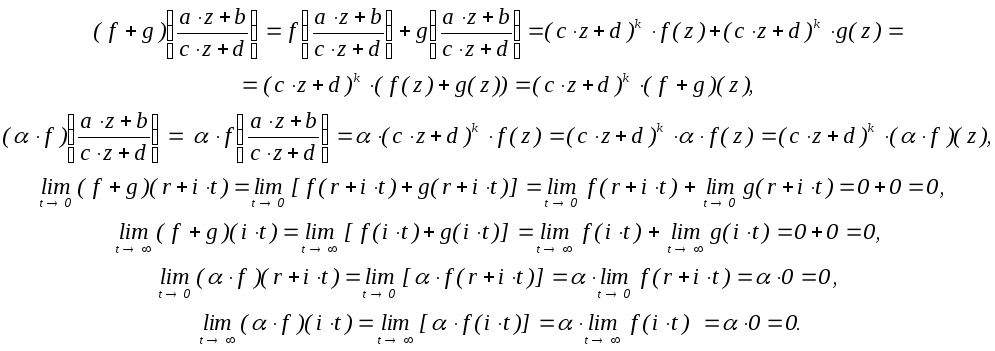
Таким образом, введённые операции, применяемые к модулярным параболическим формам веса k и уровня n, приводят снова к модулярным параболическим формам веса k и уровня n.
Каковы модулярные параболические формы веса 0 и уровня n ?
Т акая
форма удовлетворяет условию
акая
форма удовлетворяет условию![]() при любых целых a,
b,
c,
d
со свойством ad
– bcn
= 1. В частности,
при a
= 1 = d
,
с = 0 получаем
f(z
+ b)
= f(z)
при любом b
Z.
Это показывает, что функция f
однозначно
определяется своим заданием в полуполосе
0
Re(z)
< 1, Im(z)
> 0. Например,
f(–7+2i)
= = f((0
+ 2i)
– 7)
= f(0 + 2i).
при любых целых a,
b,
c,
d
со свойством ad
– bcn
= 1. В частности,
при a
= 1 = d
,
с = 0 получаем
f(z
+ b)
= f(z)
при любом b
Z.
Это показывает, что функция f
однозначно
определяется своим заданием в полуполосе
0
Re(z)
< 1, Im(z)
> 0. Например,
f(–7+2i)
= = f((0
+ 2i)
– 7)
= f(0 + 2i).
Если z
= x
+ iy,
то ![]()
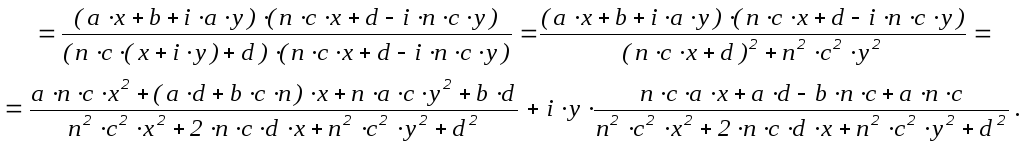
Лемма (о векторном пространстве Sk(n)). Множество Sk(n) является векторным пространством над полем C относительно следующих операций поточечного сложения и умножения на число:
+ : (f + g)(z) = f(z) + g(z), : (f)(z) = f(z).
Доказательство. Во-первых, введённые операции действительно дают модулярные параболические формы веса k и уровня n, т.е. являются алгебраическими операциями на Sk(n).
Проверим аксиомы векторного пространства.
Ассоциативность сложения: f, g, h Sk(n) (f + g) + h = f + (g + h)
Действительно, ((f + g) + h)(z) = (f + g)(z) + h(z) = f(z) + g(z) + h(z) = = f(z) + (g + h)(z) = (f + (g + h))(z), что и требовалось.
Коммутативность сложения: f, g Sk(n) f + g = g + f
В самом деле, (f + g)(z) = f(z) + g(z) = g(z) + f(z) = (g + f)(z), как и утверждалось.
Существование нейтрального элемента по сложению:
0 Sk(n) f Sk(n) 0 + f = f = f + 0
Действительно, определим функцию 0 : H H, полагая естественным образом, z H 0(z) = 0. Тогда, очевидно, что 0 Sk(n) и f Sk(n) (0 + f)(z) = 0(z) + f(z) = 0 + f(z) = f(z) и (f + 0)(z) = f(z) + 0(z) = f(z) + 0 = f(z), что и требовалось.
Существование противоположного элемента по сложению:
f Sk(n) g Sk(n) g + f = 0 = f + g
В самом деле, если определить g : H C формулой g(z) = –f(z), то, очевидно, что g Sk(n) и (f + g)(z) = f(z) + g(z) = f(z) + (–f(z)) = 0 = 0(z) и аналогично (g + f)(z) = g(z) + f(z) = (–f(z)) + f(z) = 0 = 0(z), как и должно быть.
Таким образом, (Sk(n), +) – абелева группа. Проверим аксиомы умножения на комплексные скаляры.
Свойство единицы: f Sk(n) 1f = f
Это свойство очевидно: (1f)(z) = 1f(z) = f(z), что и требовалось доказать.
Аналог ассоциативности: , C f Sk(n) ()f = (f)
В самом деле, (()f)(z) = ()f(z) = (f(z)) = ((f)(z)) = ((f))(z).
Наконец, проверим аналоги свойств дистрибутивности:
, C f Sk(n) ( + )f = f + f
C f , g Sk(n) (f + g) = f + g
Вычисляем по определению операций: (( + )f )(z) = ( + )f(z) = = f(z) + f(z) = (f)(z) + (f)(z) = (f + f)(z), как и должно было случиться.
Аналогично проверяется и второе свойство: ((f + g))(z) = ((f+g)(z)) = = (f(z) + g(z)) = f(z) + g(z) = (f)(z) + (g)(z) = (f + g)(z), что и требовалось.
Лемма доказана.
5. Вывод теоремы Ферма из гипотезы Таниямы. Пусть Великая теорема Ферма не верна, т.е. для некоторого простого числа s > 3 имеет место нетривиальное равенство a s + b s = c s, т.е. A + B = C, где A = as , B = bs , C = cs.
Рассмотрим эллиптическую кривую
y2 = x(x – A)(x – C) = x3 – (A + C)x2 + ACx
с дискриминантом
D = –(– (A + C)2(AC)2 + 4(AC)3) = –(AC)2(A – C)2 = –A2B2C2.
Пусть p
– любое
простое число, делящее ABC.
Если p
> 3, то
рациональные числа
,
µ можно
рассматривать
по модулю p:
множитель
![]() при этом следует интерпретировать как
решение сравнения3x
1 (mod
p).
Для решения этого сравнения достаточно
написать линейное разложение НОД(3,
p)
= 1 = 3u
+ pv
и заметить,
что 3u
1 (mod
p).
при этом следует интерпретировать как
решение сравнения3x
1 (mod
p).
Для решения этого сравнения достаточно
написать линейное разложение НОД(3,
p)
= 1 = 3u
+ pv
и заметить,
что 3u
1 (mod
p).
Таким образом, в случае p > 3 можно расмматривать эллиптическую кривую y2 = z3 + z + µ по модулю p, исследуя решения сравнения y2 z3 + z + µ (mod p). Пусть np – количество решений этого сравнения, т.е. количество таких пар целых чисел (r ; s), где 0 r < p, 0 s < p, что r2 s3 + s + µ (mod p). Ясно, что если для некоторого простого p рассматриваемое сравнение не имеет решений, т.е. np = 0, то на исходной эллиптической кривой не будет и рациональных точек: рациональных решений диофантова уравнения y2 = x3 + x + µ.
Итак, если p > 5 – простое число, делящее ABC, то = –(43 + 27µ2) 0 (mod p), т.е. 43 –27µ2 (mod p). Значит, и µ делятся или не делятся на p одновременно.
Если 0 µ (mod p), то A2 – AC + C2 0 (A + C)(B + C)(B – A) (mod p). Если B + C 0 (mod p), то A = C – B 2C (mod p) и значит, 0 A2 – AC + C2 3A2 (mod p), т.е. A = an и C = cn делятся на p, вопреки взаимной простоте чисел a и с. Аналогично, если B – A 0 (mod p), то получаем C = A + B 2A и 0 A2 – AC + C2 3A2 (mod p), т.е. A = an и B = bn делятся на p, вопреки взаимной простоте чисел a и b. Наконец, если A + C 0 (mod p), то 0 A2 – AC + C2 3A2 (mod p), т.е. A = an и C = cn делятся на p, вопреки взаимной простоте чисел a и с.
Поэтому можно
считать, что
![]() 0
0![]() µ (mod
p).
Пусть
– решение
сравнения 2x
–3µ
(mod
p).
Для нахождения
достаточно
написать линейное разложение НОД(2,
p)
= 1 = 2u
+ pv
и взять
= –3uµ.
Тогда
2u
1 (mod p)
и
2
= –6uµ
–3(2u)µ
–3µ
(mod p).
µ (mod
p).
Пусть
– решение
сравнения 2x
–3µ
(mod
p).
Для нахождения
достаточно
написать линейное разложение НОД(2,
p)
= 1 = 2u
+ pv
и взять
= –3uµ.
Тогда
2u
1 (mod p)
и
2
= –6uµ
–3(2u)µ
–3µ
(mod p).
Проверим, что x3 + x + µ делится на (x – )2 по модулю p. Нетрудно понять, что
x3 + x + µ = (x2 – 2x + 2)(x + 2) + (32 + )x + (23 – µ).
Таким образом, достаточно убедиться, что 32 + 0 23 – µ (mod p). Имеем по построению :
32 + = 3(–3uµ)2 + = 27µ2u2 + –43u2 + =
= –(2u)2 + – + = 0 (mod p),
23 – µ = 2(–3uµ)3 – µ = –(27µ2)(2u3µ) – µ 432u3µ – µ =
= (2u)3µ – µ µ – µ 0 (mod p).
Значит, x3
+ x
+ µ
(x
– )2(x
+ 2)
(mod
p),
причём
![]() –2
(mod
p),
т.к. иначе
0 (mod
p)
и, следовательно,
0
µ , что
невозможно.
Итак,
– двукратный,
но не трёхкратный корень этого многочлена.
–2
(mod
p),
т.к. иначе
0 (mod
p)
и, следовательно,
0
µ , что
невозможно.
Итак,
– двукратный,
но не трёхкратный корень этого многочлена.
Аналогичный факт можно доказать и для p = 2. Действительно, из 0 (mod 2) получаем –43 27µ2 (mod p), а значит, µ 0 (mod p). При этом A2 – AC + C2 A + C – AC (mod 2). Поскольку числа A = an и C = cn не могут быть одновременно чётными, то можно считать, например, что A 1 (mod 2), т.е. A + C – AC A 1 (mod 2). Поэтому x3 + x + µ x3 + x x(x2 + ) x(x + 1)2 (mod p), т.е. 1 – двукратный, но не трёхкратный корень многочлена x3 + x + µ по модулю p = 2.
Наконец, рассмотрим случай p = 3.
Если для всех простых чисел p, делящих дискриминант эллиптической кривой y2 = x3 + ax + b (a, b Z), правая часть имеет двукратный, но не трёхкратный корень по модулю p, то эта эллиптическая кривая называется полустабильной.
