
- •Министерство образования и науки Российской Федерации
- •Глава I. Азы теории чисел
- •§ 1. Деление целых чисел с остатком
- •5709 Mmmmmdссiiiiiiiii,
- •Перевод числа из десятичной системы счисления в q-ичную
- •Перевод числа из q-чной системы счисления в десятичную (схема Горнера)
- •Перевод числа из одной системы счисления в другую
- •Арифметические действия в позиционных системах счисления
- •§ 2. Деление целых чисел нацело
- •Свойства делимости нацело
- •§ 3. Наибольший общий делитель и наименьшее общее кратное
- •Основные свойства наибольшего общего делителя и наименьшего общего кратного
- •§ 4. Алгоритм Евклида
- •Расширенный алгоритм Евклида
- •§ 5. Взаимно простые числа
- •Простейшие свойства взаимно простых чисел
- •§ 6. Простые числа
- •Простейшие свойства простых чисел
- •§ 7. Простые числа в арифметических прогрессиях
- •О распределении простых чисел
- •§ 8. Язык сравнений
- •Свойства сравнений
- •§ 9. Функция Эйлера
- •§ 10. Теоремы Эйлера и Ферма
- •§ 11. Признаки делимости
- •§ 12. Принцип Дирихле
- •Глава II. Некоторые диофантовы уравнения
- •§ 1. Линейные диофантовы уравнения
- •§ 2. Общее диофантово уравнение от одного переменного
- •§ 5. Пифагоровы тройки
- •§ 6. Уравнение Ферма-Пелля
- •Глава III. Великая теорема ферма и abc – проблема
- •§ 1. Великая теорема Ферма
- •§ 2. Методы Эйлера-Куммера доказательства Великой теоремы Ферма
- •§ 3. Гипотеза Таниямы и доказательство Великой теоремы Ферма
- •§ 4. Abc – Теорема для многочленов и её следствия
- •§ 5. Abc – Гипотеза для натуральных чисел
- •§ 6. Некоторые следствия из abc– гипотезы
- •Глава IV. Задача о счастливых билетах
- •§ 1. Сведение задачи к задаче о числе наборов цифр с заданной суммой компонент
- •§ 2. Задача о числе наборов цифр с заданной суммой компонент
- •§ 3. Ещё одно решение задачи о числе наборов цифр с заданной суммой компонент
§ 2. Общее диофантово уравнение от одного переменного
Общее диофантово уравнение от одного переменного имеет следующий вид: anxn + an–1xn–1 + … + a1x + a0 = 0, где f(x) = anxn + … + a1x + a0 – многочлен с заданными целыми коэффициентами. Вопрос о решениях этого диофантова уравнения – это вопрос о целых корнях многочлена с целыми коэффициентами.
Теорема (о
рациональных корнях многочлена с целыми
коэффициентами). Если
несократимая дробь
=
![]()
Q
является корнем многочлена f(x)
= anxn+…+a1x+a0
Z[x]
степени n
с целыми коэффициентами, то p
| a0
и q
| an
.
Q
является корнем многочлена f(x)
= anxn+…+a1x+a0
Z[x]
степени n
с целыми коэффициентами, то p
| a0
и q
| an
.
Доказательство. Имеем
0 =
f()
=
![]() =
=
=
![]() (anpn
+ an–1pn–1q
+…+ aipiqn–i
+…+ a1pqn–1
+ a0qn),
(anpn
+ an–1pn–1q
+…+ aipiqn–i
+…+ a1pqn–1
+ a0qn),
anpn + an–1pn–1q + … + aipiqn–i + … + a1pqn–1 + a0qn = 0,
a0qn = p( –anpn–1 – an–1pn–2q – … – a1qn–1).
Итак, p | a0qn , причём р взаимно просто с q, а значит, и с qn (дробь несократима !). Поэтому p | a0 . Аналогично, из равенства
anpn = q(–an–1pn–1 – … – a1pqn–2 – a0qn–1)
получим, что q | an .
Теорема доказана.
Следствие (о целых корнях многочлена с целыми коэффициентами). Если целое число Z является корнем многочлена f(x) = anxn+…+a1x+a0 степени n с целыми коэффициентами, то | a0 .
Доказательство.
Целый корень
– это
несократимая дробь
![]() ,
так что из теоремы получаем
| a0
, что и
требовалось.
,
так что из теоремы получаем
| a0
, что и
требовалось.
Следствие доказано.
Примеры: 1. Найти все рациональные корни многочлена
f(x) = 2х4 + 5х3 – х2 + 5х – 3.
По доказанной
теореме, если несократимая дробь
=
![]()
Q
является корнем этого многочлена, то
р | (–3) и
q | 2 . Всегда
можно считать, что q
> 0. Поэтому
все возможные значения для p
и q
таковы p
= 1,
3;
q = 1, 2, а все
возможные значения для
соответственно
=
Q
является корнем этого многочлена, то
р | (–3) и
q | 2 . Всегда
можно считать, что q
> 0. Поэтому
все возможные значения для p
и q
таковы p
= 1,
3;
q = 1, 2, а все
возможные значения для
соответственно
=
![]() =1,
3,
=1,
3,
![]() ,
,![]() .
Устно убеждаемся, что
=1
– не корни,
= 3 также не
подходит, т.к. “в многочлене много
слагаемых с плюсом и мало с минусом”.
Легко убедиться, что
= –3 – корень:
234–533–32–53–3
= 9(29–53–1–2)
= 9(18–15–3)
= 0. Понизим
степень многочлена: 2х4+5х3–х2+5х–3
= (х+3)(2х3–х2+2х–1).
.
Устно убеждаемся, что
=1
– не корни,
= 3 также не
подходит, т.к. “в многочлене много
слагаемых с плюсом и мало с минусом”.
Легко убедиться, что
= –3 – корень:
234–533–32–53–3
= 9(29–53–1–2)
= 9(18–15–3)
= 0. Понизим
степень многочлена: 2х4+5х3–х2+5х–3
= (х+3)(2х3–х2+2х–1).
Доказанная теорема,
применённая к многочлену 2х3–х2+2х–1,
исключает возможность р
= 3.
Значит, нужно только проверить
= ![]() .
Ясно, что
=
.
Ясно, что
=
![]() – корень.
Снова понижаем степень:
2х3–х2+2х–1
= (х –
– корень.
Снова понижаем степень:
2х3–х2+2х–1
= (х –
![]() )(2х2+2),
и многочлен 2х2+2
не имеет вещественных корней. Итак,
исходный многочлен имеет два рациональных
корня:
=
)(2х2+2),
и многочлен 2х2+2
не имеет вещественных корней. Итак,
исходный многочлен имеет два рациональных
корня:
=
![]() и
= –3, один
из которых целый.
и
= –3, один
из которых целый.
2. Найти все целые корни многочлена f(x) = 3x4 – 2x2 + x +38.
Ясно, что нужно проверить делители свободного члена 38 = 219. Таких делителей четыре: ±1, ±2, ±19, ±38. Проведём вычисления по схеме Горнера:
|
fi |
3 |
0 |
–2 |
1 |
38 |
|
Si(1) |
3 |
3 |
1 |
2 |
40 |
|
Si(–1) |
3 |
–3 |
1 |
0 |
38 |
|
Si(2) |
3 |
6 |
10 |
21 |
80 |
|
Si(–2) |
3 |
–6 |
10 |
–19 |
0 |
Найден один корень = –2. Можно понизить степень, взяв коэффициенты частного от деления f(x) на x + 2 из последней строки таблицы:
f(x) = (x + 2)(3x3 – 6x2 + 10x – 19).
Целыми корнями многочлена 3x3 – 6x2 + 10x – 19 могут быть только ±1, ±19. Но ±1 уже проверены и корнями не являются, число 19 даёт явно положительное значение, а число –19 явно отрицательное.
Итак, многочлен f(x) = 3x4 – 2x2 + x +38 имеет единственный целый корень = –2.
§ 3. Диофантово уравнение x2 – y2 = a
Примеры: 1. При a = 0 получаем бесконечное число решений: x = y или x = –y для любого y Z.
2.
При a
= 1 имеем x2
– y2
= 1
(x
+ y)(x
– y)
= 1. Таким
образом, число 1
разложено в произведение двух целых
множителей x
+ y
и x
– y
(важно, что x,
y
– целые !).
Поскольку
у числа 1
всего два
разложения в произведение целых
множителей 1
= 11
и 1
= (–1)(–1),
то получаем две возможности:
![]() .
.
3.
Для a
= 2 имеем x2
– y2
= 2
(x
+ y)(x
– y)
= 2. Действуя
аналогично предыдущему, рассматриваем
разложения 2
= 12
= 21
= (–1)(–2)
= = (–2)(–1),
составляем системы:
![]() , которые, в отличие от предыдущего
примера, не имеют решений. Так что нет
решений и у рассматриваемого диофантова
уравненияx2
– y2
= 2.
, которые, в отличие от предыдущего
примера, не имеют решений. Так что нет
решений и у рассматриваемого диофантова
уравненияx2
– y2
= 2.
4.
Предыдущие рассмотрения наводят на
некоторые выводы. Решения уравнения
x2
– y2
= a
находятся по разложению a
= km
в произведение
целых чисел из системы
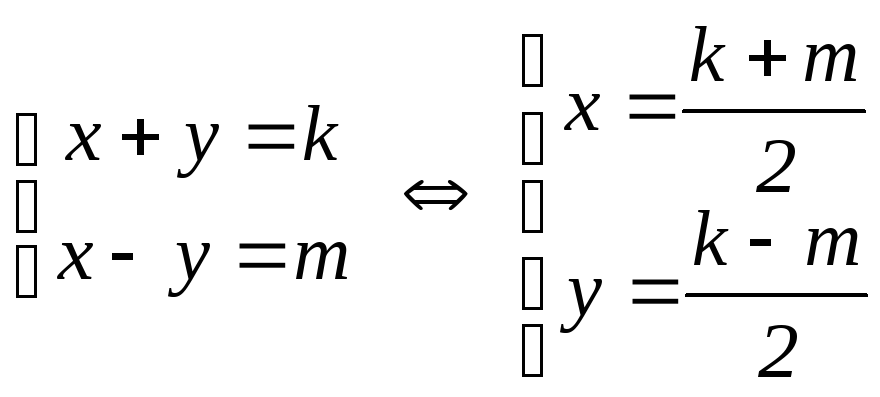 . Эта система имеет целые решения тогда
и только тогда, когдаk
+ m
и k
– m
чётны, т.е. когда числа k
и m
одной
чётности (одновременно чётны или
нечётны). Таким образом, диофантово
уравнение x2
– y2
= a
имеет решение тогда и только тогда,
когда a
допускает
разложение в произведение двух целых
множителей одной чётности. Остаётся
только найти все такие a
.
. Эта система имеет целые решения тогда
и только тогда, когдаk
+ m
и k
– m
чётны, т.е. когда числа k
и m
одной
чётности (одновременно чётны или
нечётны). Таким образом, диофантово
уравнение x2
– y2
= a
имеет решение тогда и только тогда,
когда a
допускает
разложение в произведение двух целых
множителей одной чётности. Остаётся
только найти все такие a
.
Теорема (об
уравнении x2
– y2
= a).
(1) Уравнение x2
– y2
= 0 имеет бесконечное множество решений
![]() .
.
(2) Любое решение
уравнения имеет вид 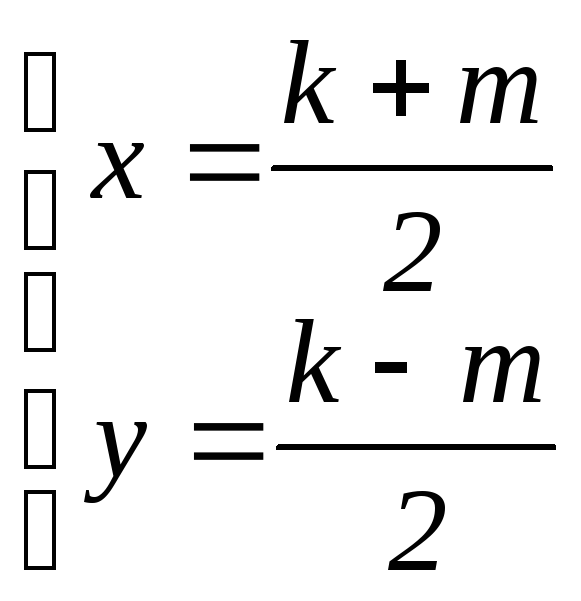 , где a
= km
– разложение числа a
в произведение целых множителей одной
чётности.
, где a
= km
– разложение числа a
в произведение целых множителей одной
чётности.
(3) Уравнение x2
– y2
= a
имеет решение тогда и только тогда,
когда a
![]() 2 (mod
4).
2 (mod
4).
Доказательство. (1) уже доказано.
(2) уже доказано.
(3)
()
Пусть вначале
диофантово уравнение
x2
– y2
= a
имеет
решение. Докажем, что a
![]() 2 (mod
4). Если a
= km
– разложение в произведение целых
чисел одной чётности, то при чётных k
и m
имеем k
= 2l,
m
= 2n
и a
= km
= 4ln
0 (mod
4). В случае
же нечётных k,
m
их произведение a
также
нечётно, разность a
– 2 нечётна
и не делится на 4,
т.е. снова a
2 (mod
4). Если a
= km
– разложение в произведение целых
чисел одной чётности, то при чётных k
и m
имеем k
= 2l,
m
= 2n
и a
= km
= 4ln
0 (mod
4). В случае
же нечётных k,
m
их произведение a
также
нечётно, разность a
– 2 нечётна
и не делится на 4,
т.е. снова a
![]() 2 (mod
4).
2 (mod
4).
()
Если теперь
a
![]() 2 (mod
4), то можно
построить решение уравнения x2
– y2
= a.
Действительно, если a
нечётно, то
a
= 1a
– разложение
в произведение целых нечётных чисел,
так что
2 (mod
4), то можно
построить решение уравнения x2
– y2
= a.
Действительно, если a
нечётно, то
a
= 1a
– разложение
в произведение целых нечётных чисел,
так что 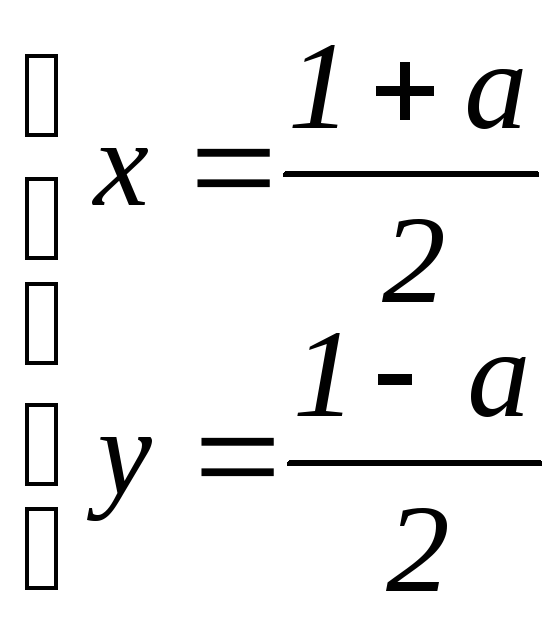 – решение диофантова уравнения. Если
же a
чётно, то
ввиду a
– решение диофантова уравнения. Если
же a
чётно, то
ввиду a
![]() 2 (mod
4) получаем,
что 4 | a,
a
= 4b
= 2(2b)
– разложение
в произведение целых чётных чисел, так
что
2 (mod
4) получаем,
что 4 | a,
a
= 4b
= 2(2b)
– разложение
в произведение целых чётных чисел, так
что ![]() –
решение диофантова уравнения.
–
решение диофантова уравнения.
Теорема доказана.
Примеры: 1. Диофантово уравнение x2 – y2 = 2012 не имеет решений, т.к. 2010 = 4502 + 2 2 (mod 4).
2. Диофантово уравнение x2 – y2 = 2011 имеет решения, т.к. 2011 3 (mod 4). Имеем очевидные разложения
2011 = 12011 = 20111 = (–1)(–2011) = (–2011)(–1),
по каждому из
которых находим решения ![]() (комбинации знаков любые). Других
решений нет, т.к. число 2011
простое
(?!).
(комбинации знаков любые). Других
решений нет, т.к. число 2011
простое
(?!).
§ 4. Диофантово уравнение x2 + y2 = a
Примеры: 1. 0 = 02 + 02, 1 = 02 + 12, k2 = 02 + k2. Таким образом, очевидно, любой квадрат тривиальным образом представим в виде суммы двух квадратов.
2. 2 = 12 + 12, 5 = 12 + 22, 8 = 22 + 22, 10 = 12 + 32, 13 = 22 + 32, 17 = 12 + 42, 18 = 32 + 32, 20 = 22 + 42, …
3. Решений нет для a = 3, 6 = 23, 7, 11, 12 = 223, 14 = 27, 15 = 35, 19, 21 = 37, 22 = 211, 23, 24 = 323, …
Анализ приведённых результатов способен навести на мысль, что отсутствие решений каким-то образом связано с простыми числами вида 4n + 3, присутствующими в разложении на множители чисел, не представимых в виде сумм двух квадратов.
Теорема (о представлении натуральных чисел суммами двух квадратов). Натуральное число a представимо в виде суммы двух квадратов тогда и только тогда, когда в его каноническом разложении простые числа вида 4n + 3 имеют чётные показатели степеней.
Доказательство.
Вначале докажем, что если натуральное
число a
представимо в виде суммы двух квадратов,
то в его каноническом разложении все
простые числа вида 4n
+ 3 должны
иметь чётные показатели степеней.
Предположим, вопреки доказываемому,
что a
= р2k+1b
= x2+y2,
где р –
простое
число вида
4n+3
и b
![]() p.
Представим числа
х и у
в виде х
= Dz,
y
= Dt,
где D
= НОД(x,
y)
= рsw,
p
p.
Представим числа
х и у
в виде х
= Dz,
y
= Dt,
где D
= НОД(x,
y)
= рsw,
p![]() w;
z,
t,
s
N0
. Тогда получаем равенство р2k+1b
= D2(z2
+ t2)
= р2sw2(z2
+ t2)
, т.е.
р2(k–s)+1b
= w2(z2
+ t2).
В левой части равенства присутствует
p
(нечётная
степень не равна нулю), значит, на простое
число p
делится
один из множителей в правой части.
Поскольку p
w;
z,
t,
s
N0
. Тогда получаем равенство р2k+1b
= D2(z2
+ t2)
= р2sw2(z2
+ t2)
, т.е.
р2(k–s)+1b
= w2(z2
+ t2).
В левой части равенства присутствует
p
(нечётная
степень не равна нулю), значит, на простое
число p
делится
один из множителей в правой части.
Поскольку p![]() w,
то р | (z2
+ t2),
где числа z,
t
взаимно
просты. Это противоречит следующей
лемме (?!).
w,
то р | (z2
+ t2),
где числа z,
t
взаимно
просты. Это противоречит следующей
лемме (?!).
Лемма (о делимости суммы двух квадратов на простое число вида 4n + 3). Если простое число р = 4n+3 делит сумму квадратов двух натуральных чисел, то оно делит каждое из этих чисел.
Доказательство.
От противного. Пусть x2
+ y2
0 (mod
p),
но x
![]() 0 или y
0 или y
![]() 0 (mod
p).
Поскольку x
и y
симметричны,
их можно менять местами, так что можно
предполагать, что x
0 (mod
p).
Поскольку x
и y
симметричны,
их можно менять местами, так что можно
предполагать, что x
![]() p.
p.
Лемма (об обратимости по модулю p). Для любого целого числа x, не делящегося на простое число p, существует обратный элемент по модулю p – такое целое число 1 u < p, что xu 1 (mod p).
Доказательство. Число x взаимно простое с p, поэтому можно записать линейное разложение НОД(x, p) = 1 = xu + pv (u, v Z). Ясно, что xu 1 (mod p), т.е. u – обратный элемент к x по модулю p. Если u не удовлетворяет ограничению 1 u < p, то поделив u с остатком на p, получим остаток r u (mod p), для которого xr xu 1 (mod p) и 0 r < p.
Лемма об обратимости по модулю p доказана.
Умножая сравнение x2 + y2 0 (mod p) на квадрат u2 обратного элемента к x по модулю p, получим
0 = 0u2 x2u2 + y2u2 = (xu)2 + (yu)2 1 + t2 (mod p).
Таким образом, для
t
= yu
выполнено
сравнение t2
–1 (mod
p),
которое и приведём к противоречию.
Ясно, что t
![]() p
: иначе t
0 (mod
p)
и 0
t2
–1 (mod
p),
что невозможно. По теореме Ферма имеем
t
p–1
1 (mod
p),
что вместе с t2
–1 (mod
p)
и p
= 4n
+ 3 приводит
к противоречию:
p
: иначе t
0 (mod
p)
и 0
t2
–1 (mod
p),
что невозможно. По теореме Ферма имеем
t
p–1
1 (mod
p),
что вместе с t2
–1 (mod
p)
и p
= 4n
+ 3 приводит
к противоречию:
1 t p–1 = t 4n+3–1 = t 2(2n+1) = (t 2)2n+1 (–1)2n+1 = –1 (mod p).
Полученное
противоречие показывает, что допущение
о x
![]() 0 (mod
p)
было не верным.
0 (mod
p)
было не верным.
Лемма о делимости суммы двух квадратов на простое число 4n+3 доказана.
Таким образом, доказано, что число, в каноническое разложение которого входит простое число p = 4n + 3 в нечётной степени, не представимо в виде суммы двух квадратов.
Докажем теперь, что любое число, в каноническом разложении которого простые числа p = 4n + 3 участвуют только в чётных степенях, представимо в виде суммы двух квадратов.
Идея доказательства основана на следующем тождестве:
(а2 + b2)(c2 + d2) = (ac – bd)2 + (ad + bc)2 ,
которое можно получить из известного свойства модуля комплексных чисел – модуль произведения равен произведению модулей. Действительно,
|z||t| = |zt| |a + bi||c + di| = |(a + bi)(c + di)|
|a + bi|2|c + di|2 = |(ac – bd) + (ad + bc)i|2
(а2 + b2)(c2 + d2) = (ac – bd)2 + (ad + bc)2 .
Из этого тождества следует, что если два числа u, v представимы в виде суммы двух квадратов: u = x2 + y2, v = z2 + t2, то и их произведение uv представимо в виде суммы двух квадратов: uv = (xz – yt)2 + (xt + yz)2.
Любое натуральное
число a
> 1 можно
записать в виде a
= р1
… рkm2
, где рi
– попарно
различные простые числа, m
N.
Для этого достаточно найти каноническое
разложение
![]() ,
записать каждую степень видаr
в виде
квадрата (r)2
при чётном
= 2,
или в виде r
= r(r)2
при нечётном
= 2
+ 1, а затем
сгруппировать отдельно квадраты и
оставшиеся одиночные простые числа.
Например,
,
записать каждую степень видаr
в виде
квадрата (r)2
при чётном
= 2,
или в виде r
= r(r)2
при нечётном
= 2
+ 1, а затем
сгруппировать отдельно квадраты и
оставшиеся одиночные простые числа.
Например,
29250 = 2325313 = 2513(35)2 , m = 15.
Число m2 обладает тривиальным представлением в виде суммы двух квадратов: m2 = 02 + m2 . Если доказать представимость в виде суммы двух квадратов всех простых чисел рi (1 i k), то используя тождество, будет получено и представление числа a. По условию, среди чисел р1 , … , рk могут встретиться только 2 = 12 + 12 и простые числа вида 4n + 1. Таким образом, осталось получить представление в виде суммы двух квадратов простого числа р = 4т + 1. Это утверждение выделим в отдельную теорему (см. ниже)
Например, для a = 29250 = 2513(15)2 последовательно получаем:
2 = 12 + 12, 5 = 12 + 22, 13 = 22 + 32,
25 = (11 – 12)2 + (12 + 11)2 = 12 + 32,
2513 = (12 – 33)2 + (13 + 32)2 = 72 + 92,
29250 = 2513(15)2 = (715)2 + (915)2 = 1052 + 1352.
Теорема доказана.
Критерий Вильсона простоты числа. Число p N простое тогда и только тогда, когда (p – 1) ! –1 (mod p).
Доказательство.
()
Если (p
– 1) !
–1 (mod
p),
но p
не простое,
то p
= mn,
где 1 <
![]() <p.
Тогда числа m,
n
участвуют
в (p
– 1) ! = 1…(p–1)
в качестве сомножителей. Значит, mu
= (p
– 1) ! = –1 + pt
= –1 + mnt
. По свойствам
делимости –1
m,
что невозможно.
<p.
Тогда числа m,
n
участвуют
в (p
– 1) ! = 1…(p–1)
в качестве сомножителей. Значит, mu
= (p
– 1) ! = –1 + pt
= –1 + mnt
. По свойствам
делимости –1
m,
что невозможно.
() Пусть теперь p – простое число. Докажем, что (p – 1)! –1 (mod p). Для p = 2, 3 это очевидно, так что будем считать, что p 5.
Пользуясь леммой об обратимости по модулю p, замечаем, что у каждого множителя x из произведения 1…x…(p–1) существует элемент обратный 1 u < p по модулю p : xu 1 (mod p). При этом элемент u тоже участвует в рассматриваемом произведении (p – 1) ! = 1…x…u…(p–1) и разным x отвечают разные обратные: если xu 1 yu (mod p), где x y, то (x – y)u 0 (mod p), т.е. p | (x – y)u, а значит, p | (x – y) или p | u, что возможно только при x = y, т.к. 0 x – y < p, 1 u < p.
Может ли оказаться, что x = u ? В этом случае x2 1 (mod p), т.е. выполнено условие (x + 1)(x – 1) 0 (mod p) значит, p | (x + 1)(x – 1), т.е. либо x + 1 p, либо x – 1 p. Это возможно только при x = 1 или x = p – 1.
Из проведённого анализа следует, что числа 2, … , p – 2 можно разбить на такие пары, что произведение чисел внутри каждой из них сравнимо с 1 по модулю p. Таким образом,
(p – 1) ! = 12…(p–2)(p–1) = 1(p–1)(x1u1)…(xkuk) 1(–1)1…1 = –1
по модулю p
(k
=
![]() ).
).
Критерий Вильсона доказан.
Примеры: 1. Для p = 5 имеем
4 ! = 1234 = 14(23) 1(–1)1 = –1 (mod 5).
2. Для p = 5 имеем
12 ! = 123456789101112 =
= 112(27)(39)(410)(58)(611) 1(–1)11111 = –1 (mod 13).
Теорема (о представлении простого числа 4n+1 в виде суммы двух квадратов). Любое простое число вида p = 4n + 1 представимо в виде суммы двух квадратов.
Доказательство. Вначале докажем, что в виде суммы двух квадратов представимо некоторое кратное числа p. Для этого используем критерий Вильсона и то, что p = 4n + 1.
Имеем
–1 (p – 1) ! = 12 … (p – 1) =
= 12 … (2n–1)(2n)(2n+1) … (4n–1)(4n)
12 … (2n–1)(2n)(–2n)(–(2n–1)) … (–2)(–1) =
= (–1)2n1222 … (2n–1)2(2n)2 = ((2n) !)2 (mod 4n + 1).
Таким образом, если K = (2n) ! , то –1 K2 (mod p), т.е. 1 + K2 0 (mod p). Это значит, что 1 + K2 = pt для некоторого целого t.
Рассмотрим теперь множество всех упорядоченных пар целых чисел
M
= {(u
; v)
Z2
| 0
![]()
k},
k},
где k
= [![]() ]
– целая
часть
]
– целая
часть
![]() ,
т.е. наибольшее целое число, не
превосходящее
,
т.е. наибольшее целое число, не
превосходящее
![]() .
.
Примеры:
[2,1] = 2, [![]() ]
= 1, [3,99] = 3, [–0,5] = –1, [–2,1] = –3.
]
= 1, [3,99] = 3, [–0,5] = –1, [–2,1] = –3.
Во множестве M содержится (k + 1)2 элементов, причём
(k
+ 1)2
= k2
+ 2k
+ 1 > (![]() – 1)2
+ 2(
– 1)2
+ 2(![]() – 1) + 1 = p.
– 1) + 1 = p.
Для каждой пары
(u
; v)
M
рассмотрим
число u
+ Kv
N0
и заметим, что все эти числа различны.
Действительно, если u1
+ Kv1
= u2
+ Kv2
, то (u1
– u2)
= K(v2
– v1),
причём |u1
– u2|
k
<
![]() =
=
![]() < K
= (2n)
! (докажите
последнее неравенство !). Поэтому u1
– u2
может
делиться на K
только при
u1
= u2
и v1
= v2
.
< K
= (2n)
! (докажите
последнее неравенство !). Поэтому u1
– u2
может
делиться на K
только при
u1
= u2
и v1
= v2
.
Итак, получили
различные между собой числа вида u
+ Kv
, количество
которых больше p
– числа остатков от деления на p.
Значит, два каких-то различных числа
u1
+ Kv1
и
u2
+ Kv2
из
рассматриваемого множества чисел дают
одинаковые остатки при делении на p.
Из u1
+ Kv1
u2
+ Kv2
(mod
p)
следует, что
![]() (mod
p),
причём, как и ранее, |u|
= |u1
– u2|
<
(mod
p),
причём, как и ранее, |u|
= |u1
– u2|
<
![]() ,
|v|
= |v1
– v2|
<
,
|v|
= |v1
– v2|
<
![]() . Тогда u2
– K2v2
= (u
+ Kv)(u
– Kv)
кратно p.
Учитывая, что K2
–1 (mod
p),
получим 0
(u
+ Kv)(u
– Kv)
= = u2
– K2v2
u2
+ v2
(mod
p).
Значит, на p
делится
число u2
+ v2
, где
0 < u2
+ v2
< 2p,
т.е. u2
+ v2
= p.
. Тогда u2
– K2v2
= (u
+ Kv)(u
– Kv)
кратно p.
Учитывая, что K2
–1 (mod
p),
получим 0
(u
+ Kv)(u
– Kv)
= = u2
– K2v2
u2
+ v2
(mod
p).
Значит, на p
делится
число u2
+ v2
, где
0 < u2
+ v2
< 2p,
т.е. u2
+ v2
= p.
Теорема доказана.
