§ 3. Ещё одно решение задачи о числе наборов цифр с заданной суммой компонент
Рассмотрим функцию
,
где для удобства считаем 0s
= 0. Умножая
приведённое выше рекуррентное соотношение
на xm+1
, получим
.
Отсюда, суммируя по всем m 1, находим
,
т.е.
,
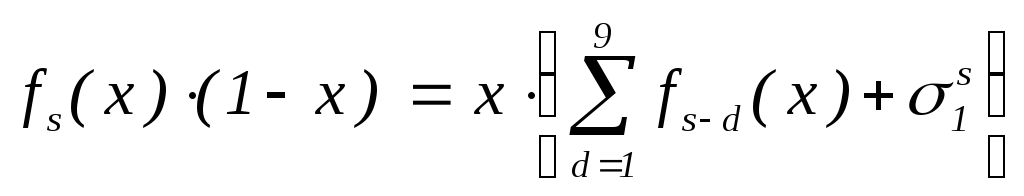или
.
Очевидно, что
fs-d(x)
0 при s
< d,
f0(x)
= x
+ x2
+ … =
, 
,
f1(x)
=
(f0(x)
+ 1) =
. Поэтому
при 1
k
8 имеем
два равенства:
Вычитая из второго
первое, получим fk+1(x)
– fk(x)
= 
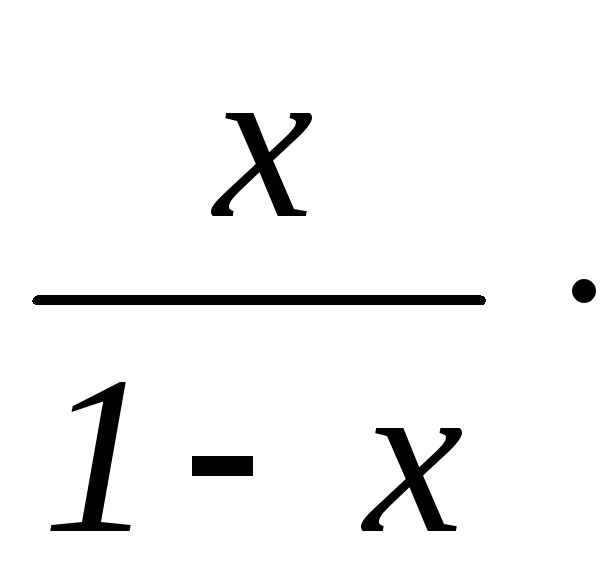fk(x),
т.е.
fk+1(x)
= 
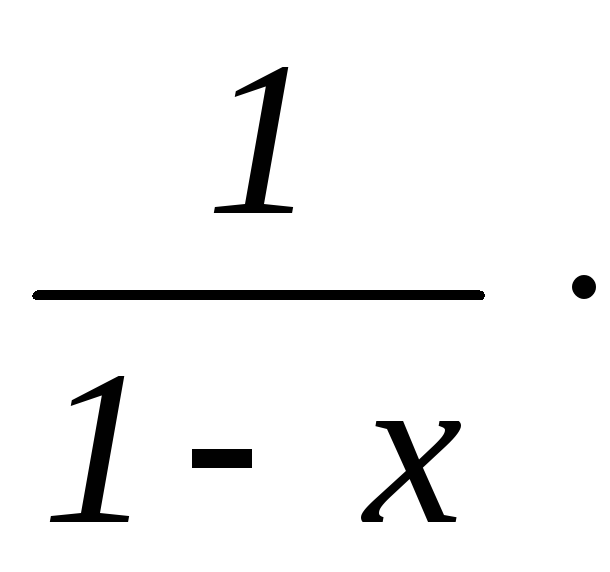fk(x),
откуда fk(x)
=
при 0
k
9.
Далее,
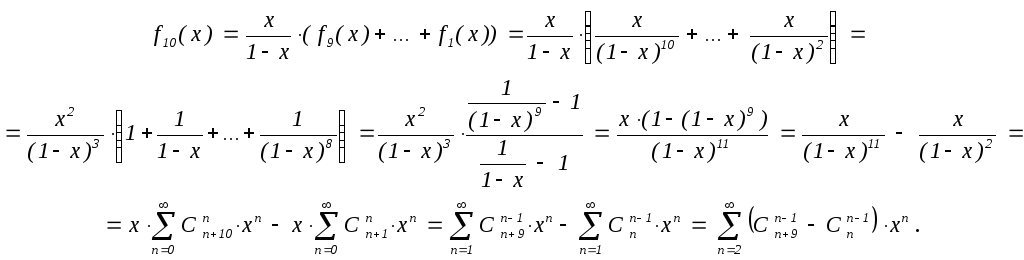
При k > 9 имеем
fk(x)
= 
(fk–1(x)
+ fk–2(x)
+ … + fk–8(x)
+ fk–9(x)),
fk+1(x)
= 
(fk(x)
+ fk–1(x)
+ … + fk–7(x)
+ fk–8(x)),
откуда после
вычитания получаем fk+1(x)
– fk(x)
= 
(fk(x)
– fk–9(x)),
т.е.
fk+10(x)
= 
(fk+9(x)
– xfk(x))
(k = 0, 1, 2, …).
В частности, при k = 1 получим
f11(x)
= 
(f10(x)
– xf1(x))
=
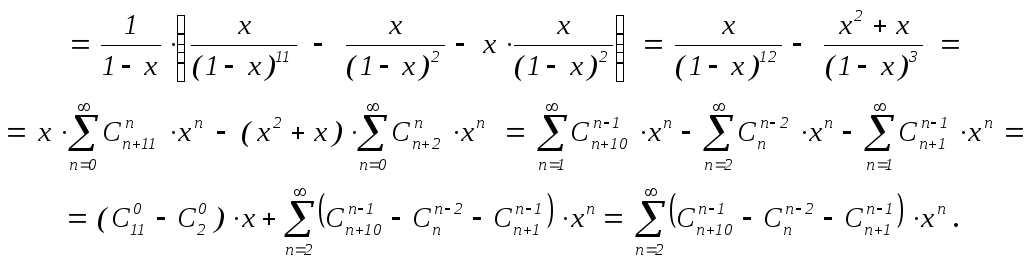
При k = 2:
f12(x)
= 
(f11(x)
– xf2(x))
=
При k = 3:
f13(x)
= 
(f12(x)
– xf3(x))
=
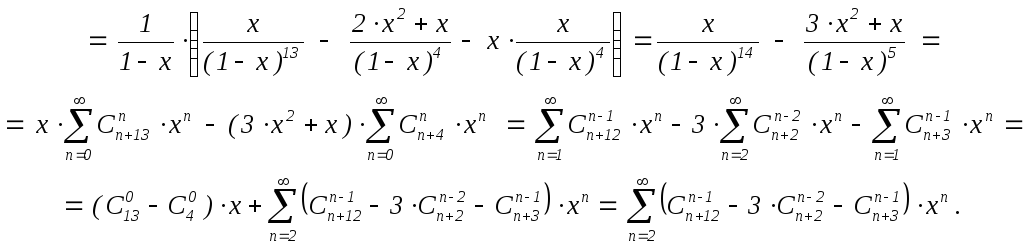
Ясно, что при 1 k 9 верны те же вычисления:
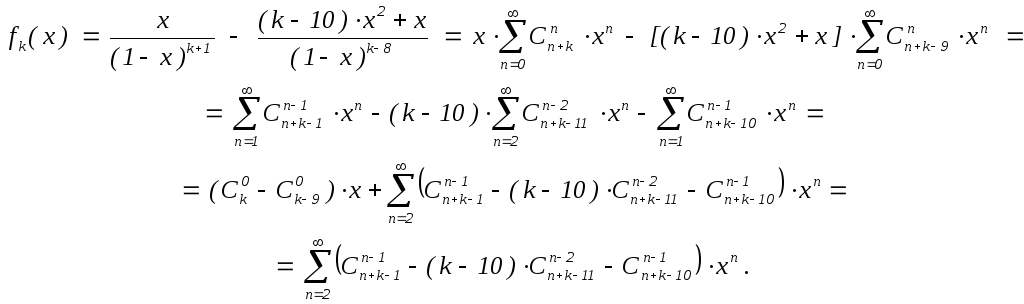Далее,
f20(x)
= 
(f19(x)
– xf10(x))
=
= 
,
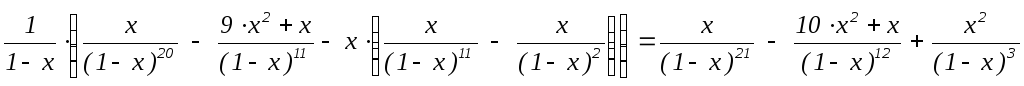f21(x)
= 
(f20(x)
– xf11(x))
=
= 
,
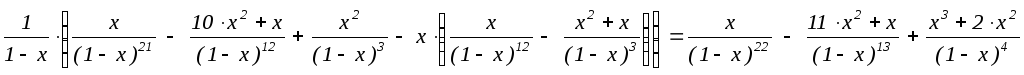f22(x)
= 
(f21(x)
– xf12(x))
=
f23(x)
= 
(f22(x)
– xf13(x))
=
f24(x)
= 
(f23(x)
– xf14(x))
=
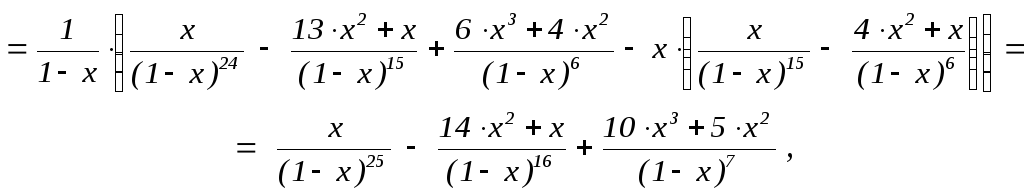
Если k = 102 + r (0 r 9), то
.
В частности, 
.
Далее, f30(x)
= 
(f29(x)
– xf20(x))
=
f31(x)
= 
(f30(x)
– xf21(x))
=
f32(x)
= 
(f31(x)
– xf22(x))
=
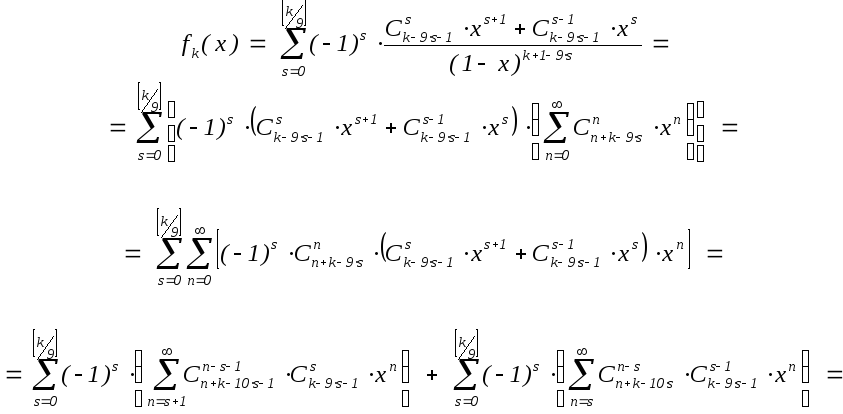
При этом
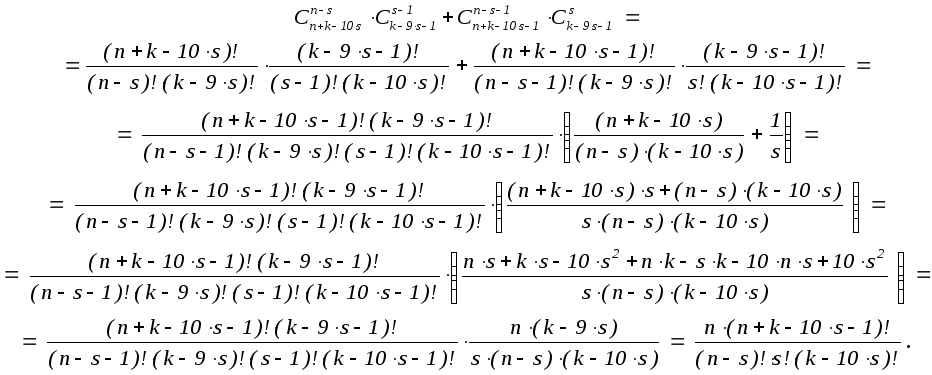
Таким образом,
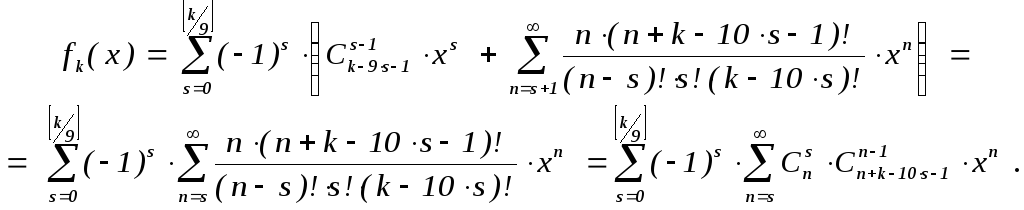
Итак,
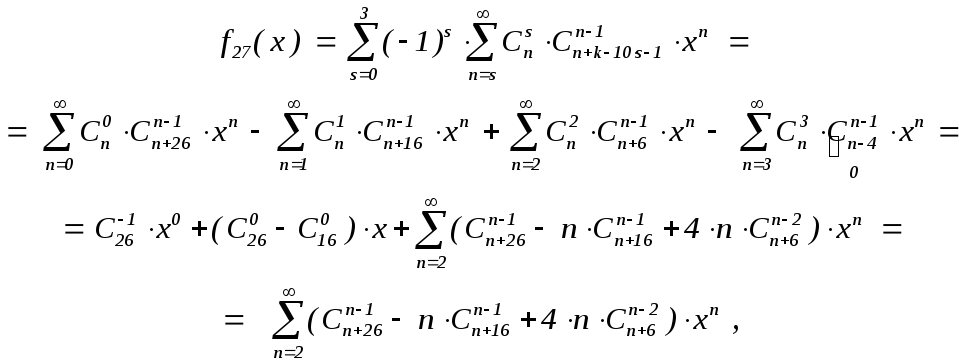
= 3231297 – 61171918 + 24495 = 201376 – 158004 + 11880 = 55252.
Л И Т Е Р А Т У Р А
Арнольд В.И. Цепные дроби. – М.: МЦНМО, 2001.
Боревич З.И., Шафаревич И.Р. Теория чисел. – М.: Наука, 1985.
Бугаенко В.О. Уравнения Пелля. – М.: МЦНМО, 2001.
Бухштаб А.А. Теория чисел. – СПб: Издательство “Лань”, 2008.
Виноградов И.М. Основы теории чисел. – СПб.: Издательство “Лань”, 2009.
Гельфонд А.О. Решение уравнений в целых числах. – М.: Наука, 1983.
Дынкин Е.Б., Успенский В.А. Математические беседы. – М.: “Физматгиз”, 1952.
Дэвенпорт Г. Высшая арифметика. – М.: Наука, 1965.
Курант Р., Робинс Г. Что такое математика ? – М. Просвещение, 1967.
Михелович Ш.Х. Теория чисел. – М.: Просвещение, 1967.
Радемахер Г., Теплиц О. Числа и фигуры. – М.: “Физматгиз”, 1962.
Серпинский В. О решении уравнений в целых числах. – М.: “Физматгиз”, 1961.
Савин А.П., Финк Л.М. Разговор в трамвае. // Квант. 1975. № 7, С. 67-70.
Серпинский В. Сто простых и одновременно трудных вопросов арифметики. – М.: “Физматгиз”, 1961.
Степанов С.А. Сравнения. – М.: Знание, 1975.
Финк Л.М. Ещё раз о счастливых билетах // Квант. 1976. № 12, С. 68-70.
Хинчин А.Я. Цепные дроби. – М.: Едиториал УРСС, 2004.
Шклярский Д.О., Ченцов Н.Н., Яглом И.М. Избранные задачи и теоремы элементарной математики. – М.: Наука, 1976.
Эдвардс Э. Последняя теорема Ферма. Генетическое введение в алгебраическую теорию чисел. – М. Мир, 1980.
Mason R.C. Diophantine Equations over Function Fields // London Math. Soc. Lecture Note Series, Vol. 96, Cambridge University Press, 1984.
Stothers W. Polynomial identities and hauptmoduln. Quart. Math. Oxford (2) 32 (1981), pp. 349–370.