
- •Министерство образования и науки Российской Федерации
- •Глава I. Азы теории чисел
- •§ 1. Деление целых чисел с остатком
- •5709 Mmmmmdссiiiiiiiii,
- •Перевод числа из десятичной системы счисления в q-ичную
- •Перевод числа из q-чной системы счисления в десятичную (схема Горнера)
- •Перевод числа из одной системы счисления в другую
- •Арифметические действия в позиционных системах счисления
- •§ 2. Деление целых чисел нацело
- •Свойства делимости нацело
- •§ 3. Наибольший общий делитель и наименьшее общее кратное
- •Основные свойства наибольшего общего делителя и наименьшего общего кратного
- •§ 4. Алгоритм Евклида
- •Расширенный алгоритм Евклида
- •§ 5. Взаимно простые числа
- •Простейшие свойства взаимно простых чисел
- •§ 6. Простые числа
- •Простейшие свойства простых чисел
- •§ 7. Простые числа в арифметических прогрессиях
- •О распределении простых чисел
- •§ 8. Язык сравнений
- •Свойства сравнений
- •§ 9. Функция Эйлера
- •§ 10. Теоремы Эйлера и Ферма
- •§ 11. Признаки делимости
- •§ 12. Принцип Дирихле
- •Глава II. Некоторые диофантовы уравнения
- •§ 1. Линейные диофантовы уравнения
- •§ 2. Общее диофантово уравнение от одного переменного
- •§ 5. Пифагоровы тройки
- •§ 6. Уравнение Ферма-Пелля
- •Глава III. Великая теорема ферма и abc – проблема
- •§ 1. Великая теорема Ферма
- •§ 2. Методы Эйлера-Куммера доказательства Великой теоремы Ферма
- •§ 3. Гипотеза Таниямы и доказательство Великой теоремы Ферма
- •§ 4. Abc – Теорема для многочленов и её следствия
- •§ 5. Abc – Гипотеза для натуральных чисел
- •§ 6. Некоторые следствия из abc– гипотезы
- •Глава IV. Задача о счастливых билетах
- •§ 1. Сведение задачи к задаче о числе наборов цифр с заданной суммой компонент
- •§ 2. Задача о числе наборов цифр с заданной суммой компонент
- •§ 3. Ещё одно решение задачи о числе наборов цифр с заданной суммой компонент
Глава IV. Задача о счастливых билетах
Речь идёт, конечно, о счастливых автобусных билетах. Как известно, каждый такой билет однозначно определяется своим шестизначным номером a b c d e f , причём a + b + c = d + e + f. Цель этой главы – вычислить количество счастливых билетов.
§ 1. Сведение задачи к задаче о числе наборов цифр с заданной суммой компонент
Ясно, что задача допускает естественное обобщение: вместо шестизначных номеров можно рассматривать произвольные 2n-значные наборы вида (a1 ; … ; an ; b1 ; … ; bn), где a1 + … + an = b1 + … + bn .
Лемма. Существует взаимно однозначное соответствие между всеми счастливыми 2n-наборами и всеми 2n-наборами с суммой цифр 9n .
Доказательство. Пусть D = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} – множество всех десятичных цифр,
Hn = {(a1 ; … ; an ; b1 ; … ; bn) D2n | a1 + … + an = b1 + … + bn }
– множество всех счастливых 2n-наборов, и
∑ 9n = {(a1 ; … ; an ; b1 ; … ; bn) D2n | a1 + … + an + b1 + … + bn = 9n }
множество всех 2n-наборов с суммой цифр 9n.
Рассмотрим отображение 2n-наборов, заданное следующим правилом:
f(a1 ; … ; an ; b1 ; … ; bn) = (a1 ; … ; an ; 9 – b1 ; … ; 9 – bn).
Таким образом, каждому 2n-набору отображение f ставит в соответствие однозначно определённый 2n-набор.
При этом отображение f инъективно, т.е. переводит разные наборы в разные: если
f(a1 ; … ; an ; b1 ; … ; bn) = f(с1 ; … ; сn ; d1 ; … ; dn),
то (a1 ; … ; an ; 9 – b1 ; … ; 9 – bn) = (c1 ; … ; cn ; 9 – d1 ; … ; 9 – dn), а значит, (a1 ; … ; an ; b1 ; … ; bn) = (с1 ; … ; сn ; d1 ; … ; dn).
Отображение f сюръективно: если (с1 ; … ; сn ; d1 ; … ; dn) – любой 2n-набор, то f(с1 ; … ; сn ; 9 – d1 ; … ; 9 – dn) = (с1 ; … ; сn ; d1 ; … ; dn).
Таким образом, f – биективное отображение.
Кроме того, если применить f к счастливому набору, для которого выполняется a1 + … + an = b1 + … + bn , то получается набор с суммой цифр a1 + … + an + (9 – b1) + … + (9 – bn) = 9n. Значит, f биективно отображает множество Hn в ∑ 9n : f : Hn ∑ 9n .
Лемма доказана.
Эта лемма показывает, что количество счастливых 2n-наборов равно количеству 2n-наборов с суммой цифр 9n. Можно теперь поставить более общую задачу: сколько m-наборов имеют сумму цифр s ?
§ 2. Задача о числе наборов цифр с заданной суммой компонент
Если искомое количество обозначить через ms , то
ms = 0 при s > 9m и при s < 0,
m0
= 1, m1
= m, m2
=
![]() ,
,
1i = 1 (0 i 9), 1i = 0 (i 10),
m+1s = ms + ms–1 + ms–2 + ms–3 + ms–4 + ms–5 + ms–6 + ms–7 + ms–8 + ms–9.
Последняя формула,
справедливая при любом m
N,
следует из того, что в любом наборе (a1
; a2
;… ; am+1)
с суммой компонент s
на первом месте стоит одна из цифр 0
a1
9, а сумма
компонент “хвоста”
(a2
;… ; am+1)
равна s
– a1
. Таким
образом,
![]() .
.
Пусть ![]() (m-набор
не может иметь сумму компонент, большую
9m).
Ясно, что
(m-набор
не может иметь сумму компонент, большую
9m).
Ясно, что
g1(x) = 1x0 + 1x1 + … + 1x9 = 1 + x1 + … + x9,
g2(x) = 1x0 + 2x1 + 3x2 + 4x3 + 5x4 + 6x5 + 7x6 + 8x7 + 9x8 + 10x9 +
+ 9x10 + 8x11 + 7x12 + 6x13 + 5x14 + 4x15 + 3x16 + 2x17 + 1x18.
При вычислении g2(x) учитывалось, что пары (a; b) с суммой s при 0 s 9 исчерпываются следующими: (0; s), (1; s–1), … , (s–1; 1), (s; 0) и их количество s + 1, а при 10 s 18 таковыми будут пары (s–9; 9), (s–10; 8), … , (8; s–10), (9; s–9) и их число |(s–9)–9| + 1 = |s–18| + 1 = 19–s.
Лемма (о связи gm(x) и g1(x)). gm(x) = g1(x)m .
Доказательство. Индукция по m. База для m = 1 верна.
Пусть доказано, что gm(x) = g1(x)m для m = 1, … , k N. Докажем, что gk+1(x) = g1(x)k+1 . По предположению индукции
gk(x) = g1(x)k = g0 + g1x + … + g9kx9k .
Тогда g1(x)k+1 = (1 + x + x2 + … + x9)(g0 + g1x + … + g9kx9k) =
= 1g0 + (1g1+1g0)x + … + (1g9k–1+1g9k)x9k+8 + 1g9kx9(k+1).
Здесь при xi
стоит сумма
1gi
+ 1gi–1
+ … + 1gi–9
в соответствии
с формулой умножения многочленов,
которая удобнее записывается для рядов
в следующем виде:
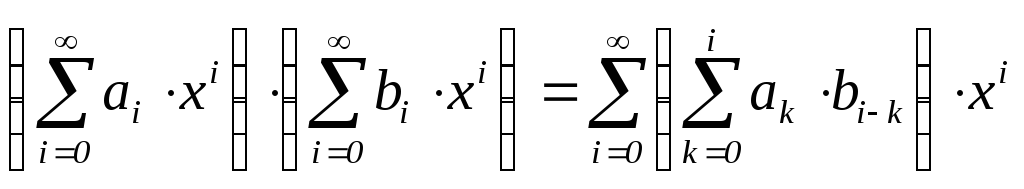 .
.
По смыслу gi – это по предположению индукции количество k-наборов с суммой компонент i : gi = ki. Как вычислить число k+1j всех (k+1)-наборов с суммой компонент j ? Ответ даёт рекуррентная формула из начала параграфа:
k+1j = kj + kj–1 + kj–2 + kj–3 + kj–4 + kj–5 + kj–6 + kj–7 + kj–8 + kj–9,
совпадающая с приведённым выше правилом вычисления коэффициентов многочлена g1k+1. Значит, k+1j равно j-му коэффициенту многочлена g1k+1.
Лемма доказана.
Итак, нужно вычислить
(1 + x
+ x2
+ … +
x9)m
=
![]() =
=
=
(1 – x10)m(1
– x)–m
=
 =
=
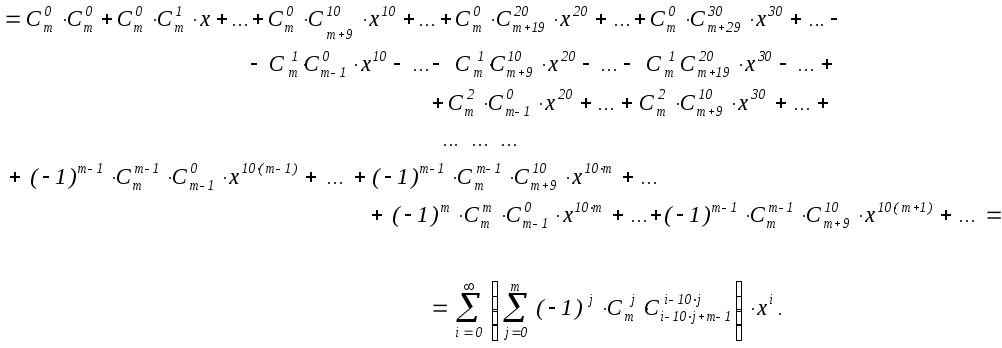
Здесь использована
формула (1 –
y)–k
=
![]() , а также соглашение
, а также соглашение![]() = 0 при p
< 0, при q
< 0, при q
> p.
= 0 при p
< 0, при q
< 0, при q
> p.
Итак, 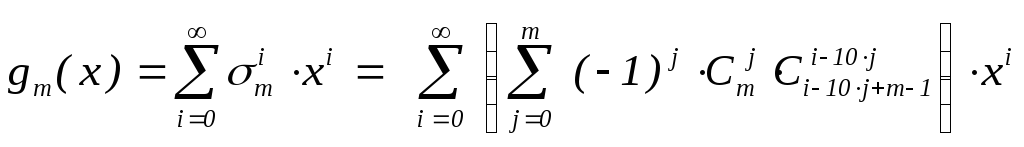 ,
т.е. mi
– коэффициент
при xi
в полученном
разложении. Итак,
,
т.е. mi
– коэффициент
при xi
в полученном
разложении. Итак,
ms
=  .
.
В частности,
627
=
![]() =
=
= ![]() =
=
= 7293132 – 18192122 + 9101112 = 201376 – 158004 + 11880 = 55252.
