Приклади розв`язку задач

1.61. Знайти добуток А В та В А двох матриць

 

Добуток А В не існує, бо число стовпців матриці А не дорівнює числу рядків матриці В. Число стовпців матриці В дорівнює числу рядків матриці А. Отже існує добуток В А:

 

1.62. Знайти матрицю 2А+5В, якщо

 

 

 

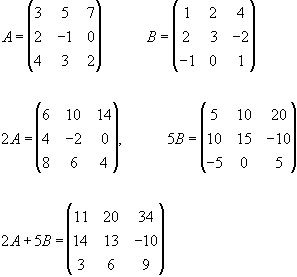
§ 8 Обернена матриця, розв`язок матричних рівнянь

При розгляді дій з матрицями не вводиться операція ділення. Але можливо ввести поняття, яке дозволяє дати деякий еквівалент цій дії.

Визначення. Квадратна матриця В називається оберненою квадратній матриці А, якщо добуток А· В є одинична матриця.

Доведемо, що для будь-якої квадратної матриці А, визначник якої відмінний від нуля, існує одна і тільки одна обернена матриця, і приведемо спосіб її обчислення.

Нехай задана матриця

 

 

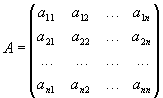
Нехай

 

є шукана матриця і 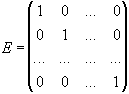- одинична матриця того ж порядку n.

Згідно умови А· В=Е, тому для визначення n² елементів b_ік матриці В ми маємо n систем рівнянь першого порядку, кожна з яких містить n рівнянь:

 

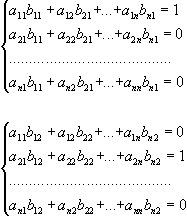
Такі системи мають одну і ту ж основну матрицю А.

Згідно припущення , тому кожна система має єдиний розв`язок, який можливо обчислити за формулами Крамера. Оскільки в правій частині в кожній системі тільки один елемент дорівнює одиниці, а всі інші дорівнюють нулю, тоді

і взагалі , i,k=1,2,...,n.

 

Отже, матриця В, обернена матриці А, яка позначається частіше символом А^-1, має вигляд

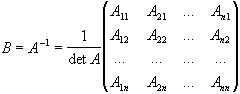 (1)

 

Раніше було вказано, що взагалі кажучи, для довільних матриць А і В . Але можливо довести, що А^-1· А=А· А^-1.

 

Дійсно 

 

Але сума добутків елементів будь-якого рядка матриці на алгебраїчне доповнення відповідних елементів другого рядка дорівнює нулю, а сума добутків елементів будь-якого рядка матриці на відповідні алгебраїчні доповнення елементів того ж рядка дорівнює самому визначнику.

Тому 

 

і отже, А^-1· А=Е=А· А^-1

Поняття “обернена матриця” може бути використано для розв`язку матричних рівнянь.

Нехай, наприклад, задане рівняння АХ=В, де А і В - задані квадратні матриці порядку n, а Х - шукана квадратна матриця того ж порядку. Нехай . Тоді обчислюємо матрицю А^-1 і помножимо ліву і праву частини заданого рівняння зліва на А^-1:

 

А^-1 *(А Х)=А^-1 *В

Оскільки

А^-1 *(А Х)=(А^-1 *А) Х

(згідно асоціативної властивості множення матриць), тоді

А^-1 *(А Х)=Е Х=Х

і одержуємо

Х=А^-1 *В

Для обчислення матриці А^-1 , оберненої матриці А, можливо, звичайно, використати формули (1). Але, як правило, значно вигідніше використати для цього метод повного виключення. Це доцільно ще і тому, що всі n систем рівнянь, які служать для визначення стовпців матриці А^-1 , відрізняються тільки правими частинами. Тому процес перетворення розширених матриць цих систем можна проводити одночасно для всіх матриць.

6. Як розв`язується система лінійних рівнянь у матричному вигляді з використанням оберненої матриці?

Іі. Приклади розв`язку задач

1.67. Знайти матрицю, обернену матриці

 

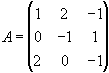
Розглянемо матрицю

 

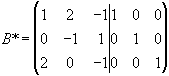
Перші три стовпці цієї матриці - стовпці заданої матриці А, наступні три стовпці, відділені рискою і складають разом одиничну матрицю, - стовпці вільних членів для систем рівнянь, які визначають елементи оберненої матриці.

Проводимо звичайні операції методу повного виключення:

 

Матриця, відокремлена рискою, і є шукана, оскільки кожний її стовпець є розв`язком відповідної системи рівнянь, тобто

 

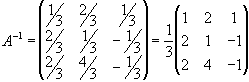
1.68. Знайти матрицю, обернену матриці

 

Розглянемо матрицю

 

 

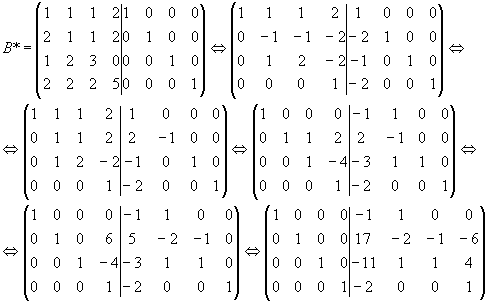
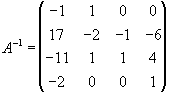
Другий спосіб знаходження оберненої матриці.

1.69. Знайти обернену А^-1 матрицю до матриці А.

 

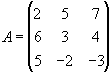
Обчислимо визначник матриці А:

 

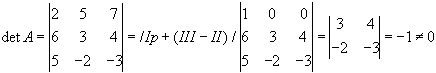
Матриця А неособлива, оскільки

 

Обчислимо алгебраїчні доповнення елементів цього визначника

 

Згідно формули (1) записуємо А^-1

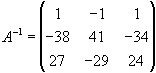
1.70. Знайти матрицю обернену до даної

 

Запишемо обернену матрицю у вигляді

 

Згідно правила множення матриць одержимо

Для знаходження елементів матриці А^-1 запишемо системи

 

 

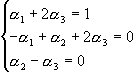
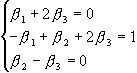
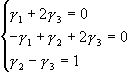
Розв`язки цих систем і дають нам елементи оберненої матриці

 

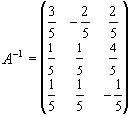
1.71. Знайти матрицю Х з рівняння

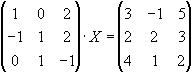
Помножимо обидві частини рівняння з лівого боку на матрицю, обернену до матриці 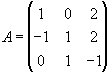. Згідно попереднього прикладу .

 

В лівій частині рівняння в силу асоціативного закону маємо:

У правій частині буде

 

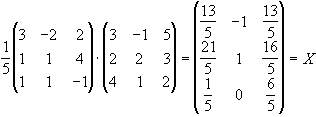
Зауваження. Оскільки множення матриць некомутативне А В В А, то в задачах такого типу потрібно уважно визначати, з якого боку слід множити, обидві частини рівняння на матрицю, обернену до однієї з даних.

1.72. Розв`язати систему рівнянь

 

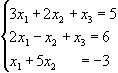
представивши її у вигляді матричного рівняння.

Перепишемо систему у вигляді АХ=В, де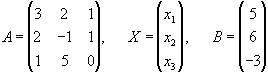 

 

Розв`язок матричного рівняння має вигляд Х=А^-1В. Знайдемо А^-1. Маємо

 

Обчислимо алгебраїчне доповнення елементів цього визначника.

 

Згідно (1)

 

Отже,

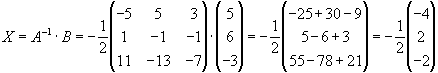
, тобто х₁=2, х₂=-1, х₃=1